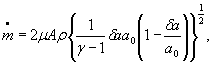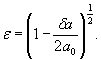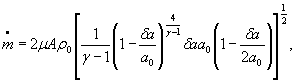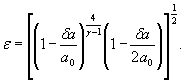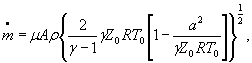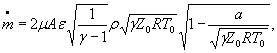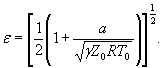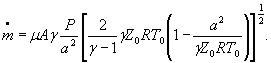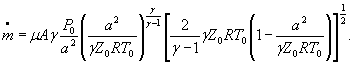ГОСТ 8.464-82 Государственная система обеспечения единства измерений. Расход газа массовый.

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
РАСХОД ГАЗА МАССОВЫЙ.
РАСЧЕТНЫЕ
ЗАВИСИМОСТИ КОСВЕННЫХ МЕТОДОВ
ИЗМЕРЕНИЙ
ГОСТ 8.464-82
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СС С Р ПО СТАНДАРТАМ
Москва
СОДЕРЖАНИЕ
|
1. ТЕРМОГАЗОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ 2. РАСЧЕТНЫЕ ЗАВИСИМОСТИ 3. ТРЕБОВАНИЯ К ПОРЯДКУ ПОЛУЧЕНИЯ ИСХОДНЫХ ФОРМУЛ ДЛЯ ОЦЕНКИ ПОГРЕШНОСТИ ИЗМЕРЕНИЯ МАССОВОГО РАСХОДА ПРИЛОЖЕНИЕ Справочное ПРИМЕР ПОЛУЧЕНИЯ ИСХОДНЫХ ФОРМУЛ ДЛЯ РАСЧЕТА ПОГРЕШНОСТИ ИЗМЕРЕНИЯ МАССОВОГО РАСХОДА ГАЗА
|
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
|
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ РАСХОД
ГАЗА
МАССОВЫЙ. State
system for ensuring the uniformity of |
ГОСТ 8.464-82 |
Постановлением Государственного комитета СССР по стандартам от 23
апреля
с 01.07.33
Настоящий стандарт устанавливает комплекс расчетных зависимостей между массовым расходом стационарного изоэнтропического энергоизолированного однофазного потока газа, термогазодинамическими параметрами, параметрами состояния, физическими константами, эмпирическими коэффициентами и геометрическими размерами «проточных каналов, а также требования к порядку получения исходных формул для оценки погрешности измерения массового расхода.
Настоящий стандарт обязателен для применения при разработке средств измерений массового расхода газа, регламентированных к использованию ГОСТ 8.369-79, соответствующих стандартов методик выполнения измерений и нормативно-технических документов на методы и средства поверки.
Расчетные зависимости для массового расхода газа, регламентированные настоящим стандартом, могут быть преобразованы в расчетные зависимости для объемного расхода газа, приведенного к нормальным условиям, установленным ГОСТ 2939-63. С этой целью зависимости для массового расхода газа делят на плотность газа «при нормальных условиях q h или на уравнение, выражающее эту плотность газа через давление, температуру, газовую постоянную и коэффициент сжимаемости q h = P Н / Z Н RT H .
1. ТЕРМОГАЗОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ
1.1. Сочетания независимых термогазодинамических параметров, измеряемых прямым методом, используемые в расчетных зависимостях для массового расхода газа, выбраны из следующего рада термогазодинамичеоких параметров:
а 0 ; а ;
w ; δа = а0 - а; δ w 0 = а0 - w ; δ w
= а
- w ;
ρ 0 ; ρ; δρ = ρ0
- ρ;
Р0; Р; δ p = p 0 - p ;
Т 0 ,
где а - скорость звука;
ρ - плотность газа;
Р - абсолютное давление в -потоке;
w - скорость потока;
Т 0 - температура потока.
Индекс «0» означает, что значение параметра соответствует состоянию изоэнтропического заторможенного потока.
2. РАСЧЕТНЫЕ ЗАВИСИМОСТИ
2.1. Расчетные зависимости для массового расхода в исходной и упрощенной формах, выражения для поправочных множителей ε, условные обозначения расчетных зависимостей в виде литеры М с верхним и нижним цифровыми индексами, сочетания независимых термогазодинамических параметров, подлежащих измерениям прямым методом, и параметры A , γ , Z 0 , R , μ, численные значения которых предполагаются известными, представлены в таблице.
|
Условное обозначение расчетных зависимостей. |
Сочетания измеряемых термогазодинамических параметров |
Расчетные
зависимости |
|
|
ρ , ω |
m = μAρ ω |
|
|
ρ 0 ; ω,
P0 |
|
|
|
ρ 0 ; ω,
a0 |
|
|
|
ρ 0 ; δω0,
a0 |
|
|
|
ρ 0 ; ω,
a0 |
|
|
|
ρ 0 ; δω,
a0 |
|
|
|
ω , P, T0 |
|
|
|
ω , P,
a0 |
|
|
|
δω0, P, a0 (μ, A, γ ) |
|
|
|
ω , P, a (μ, A, γ ) |
|
|
|
δω0, P, a |
|
|
|
ω , P0, T0 |
|
|
|
ω , P, a0 |
|
|
|
δω0, P, a0 |
|
|
|
ω , P0, a |
|
|
|
δω, P0, a0 |
|
|
|
ρ , P,
P0 |
|
|
|
ρ , δP,
P0 |
|
|
|
ρ 0 , P,
P0 |
|
|
|
ρ 0 , δP,
P0 |
|
|
|
ρ , ρ 0 , P0 |
|
|
|
δρ , ρ 0 , P0 |
|
|
|
ρ , ρ 0 , P |
|
|
|
δρ , ρ 0 , P0 |
|
|
|
P , P0, T0 |
|
|
|
δ P , P0, T0 |
|
|
|
P , P0, ρ |
|
|
|
δ P , P0, ρ |
|
|
|
ρ , P0,
T0 |
|
|
|
ρ , P,
T0 |
|
|
|
ρ , α , α 0 |
|
|
|
ρ , δα , α 0 |
|
|
|
ρ , δα , α 0 |
|
|
|
ρ , α , T0 |
|
|
|
P , α , T0 |
|
|
|
P 0 , α , T0 |
|
Обозначения:
А - площадь проходного сечения канала;
γ - показатель изоэнтропы;
z 0 - коэффициент сжимаемости изоэнтропически заторможенного газа;
R - удельная газовая постоянная;
μ - коэффициент расхода;
![]() - массовый
расход газа.
- массовый
расход газа.
3. ТРЕБОВАНИЯ К ПОРЯДКУ ПОЛУЧЕНИЯ ИСХОДНЫХ ФОРМУЛ ДЛЯ ОЦЕНКИ ПОГРЕШНОСТИ ИЗМЕРЕНИЯ МАССОВОГО РАСХОДА
3.1. Значение относительного среднего
квадратического отклонения случайной составляющей погрешности измерения
массового расхода на основе расчетной зависимости ![]() рассчитывают по формуле
рассчитывают по формуле
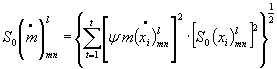 , (1)
, (1)
|
где х i |
- обобщенный символ параметров в расчетной
зависимости |
|
|
- относительные средние квадратические отклонения случайных составляющих погрешностей измерения параметра х i ; |
|
|
- коэффициенты влияния погрешностей измерения параметров на погрешность измерения массового расхода; |
|
t |
- число параметров
в расчетной зависимости |
3.2. Коэффициенты влияния ![]() определяют то формуле
определяют то формуле
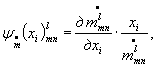 , (2)
, (2)
|
где
|
- частные производные от массового расхода,
выраженного расчетной зависимостью |
3.3.
Относительное среднее квадратическое отклонение случайной составляющей
погрешности поправочного множителя ![]() рассчитывают по формуле
рассчитывают по формуле
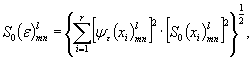 (3)
(3)
|
где
|
- коэффициенты влияния погрешностей измерения
параметров х i в выражениях для поправочных множителей |
|
r |
-
число параметров х i в выражениях для |
3.4. Коэффициенты влияния ![]() определяют по формуле
определяют по формуле
![]() , (4)
, (4)
где ![]() - частные производные от поправочного
множителя по параметрам х i .
- частные производные от поправочного
множителя по параметрам х i .
3.5. Пределы относительной неисключенной систематической составляющей погрешности результата намерения массового расхода рассчитывают по формуле
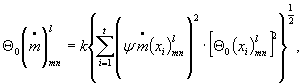 (5)
(5)
|
где
|
- пределы относительных неисключенных систематических составляющих погрешностей параметров х i ; |
|
k |
- коэффициент, определяемый в соответствии с ГОСТ 8.207-76. |
Пределы относительной
неисключенной систематической составляющей погрешности поправочного множителя ![]() рассчитывают по
формуле
рассчитывают по
формуле
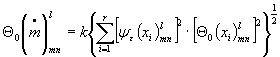 , (6)
, (6)
Пределы суммарной погрешности результата измерения расхода рассчитывают по методике, регламентированной ГОСТ 8.207-76.
Пример получения исходных формул для расчета погрешности измерения массового расхода газа приведен в справочном приложении.
ПРИЛОЖЕНИЕ
Справочное
ПРИМЕР ПОЛУЧЕНИЯ ИСХОДНЫХ ФОРМУЛ ДЛЯ РАСЧЕТА
ПОГРЕШНОСТИ ИЗМЕРЕНИЯ МАССОВОГО РАСХОДА ГАЗА
Для расчетной зависимости ![]()
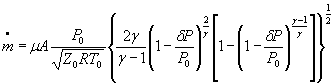
или
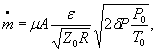
где 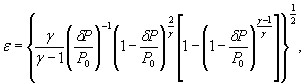
формулы (1) и (3) настоящего стандарта записывают в виде
|
S 0 ( +
[ |
(1) |
и
|
S 0 ( + [ |
(2) |
|
где S 0 (ε)={[ψε( δP )∙ S 0 ( δP )]2 + [ψε ( P 0 )∙ S 0 ( P 0 )]2
+ ψε ( γ )∙ S 0 ( γ )]2} |
(3) |
Коэффициенты влияния в формуле ( 1) равны;
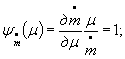
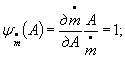
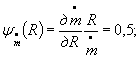
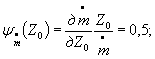
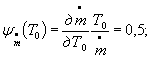
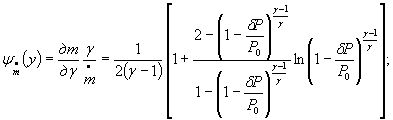
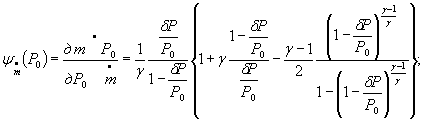
![]()
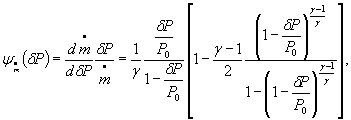
в формулах (2) и (3)
![]() ;
;
![]() ;
;
![]()
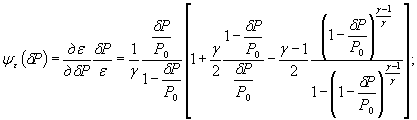
![]()
Зависимости абсолютных значений
коэффициентов влияния ![]() ,
, ![]() ,
, ![]() ,
, ![]() и поправочного
множителя ε от относительной
разности давлений δР/Р0 для различных показателей
изоэнтропы γ могут быть рассчитаны заранее и
представлены в виде таблиц или графиков.
и поправочного
множителя ε от относительной
разности давлений δР/Р0 для различных показателей
изоэнтропы γ могут быть рассчитаны заранее и
представлены в виде таблиц или графиков.
Для газов с показателем изоэнтропы γ =1,4 такие зависимости приведены на чертеже.
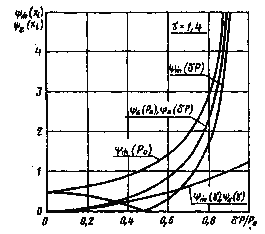
Если при измерении массового расхода газа относительные разности между давлением изоэнтропически заторможенного газа и статическим давлением δР/Р0 = (Р0 - Р)/Р0 изменяются, например от 0,01 до 0,02, то коэффициенты влияния могут быть приняты равными
![]() = 0,490;
= 0,490;
![]() = 0,510;
= 0,510;
![]() = 0,008 ;
= 0,008 ;
![]() =
= ![]() = 0,010.
= 0,010.
Тогда формулы (1) - (3) можно записать соответственно в виде
S 0 =( ![]() )={S0( μ )2 + S0(A)2+0,000064 S 0 (γ)2+0,25[S0(R)2+S0(Z0)2+ S0(T0)2]+
)={S0( μ )2 + S0(A)2+0,000064 S 0 (γ)2+0,25[S0(R)2+S0(Z0)2+ S0(T0)2]+
+ 0,24 S0(δP)2+0,26 S0(P0)2} ![]()
S 0 ( ![]() )-{ S 0 ( μ )2+ S 0 (A)2+ S 0 (ε)2+0,25
[S0(R)2+ S 0 (Z0)2+ S 0 (T0)2+ S 0 ( δ Р )2+ S 0 (P0)2}
)-{ S 0 ( μ )2+ S 0 (A)2+ S 0 (ε)2+0,25
[S0(R)2+ S 0 (Z0)2+ S 0 (T0)2+ S 0 ( δ Р )2+ S 0 (P0)2} ![]() ,
,
S 0 (ε)-={0,0001 [S0( δP)2+S0(P0)2+0,000064 S0( γ)2} ![]() .
.
Аналогично находят числовые значения коэффициентов влияния в формуле (4) настоящего стандарта при оценке относительной неисключенной систематической составляющей погрешности.
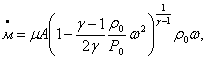
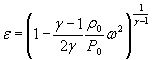
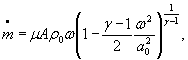
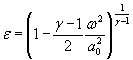
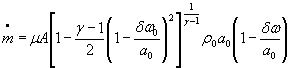
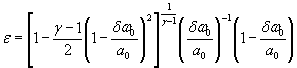
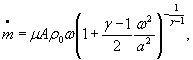
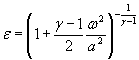
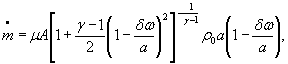
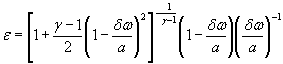
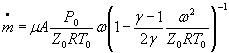
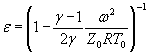
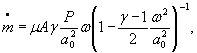
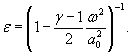
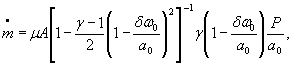
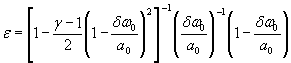
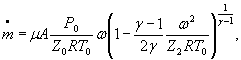
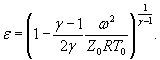
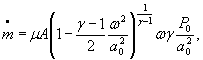
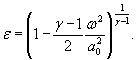
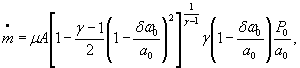
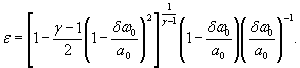
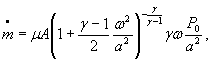
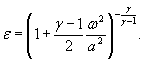
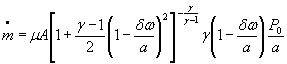
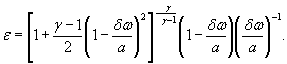
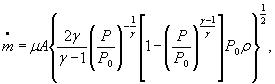
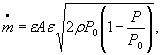
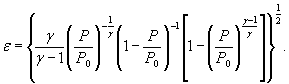
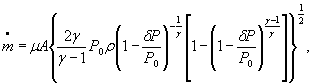
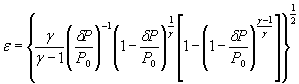
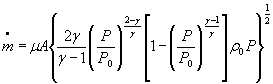
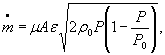
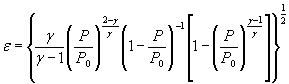
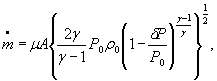
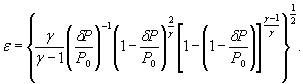
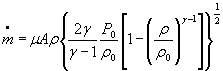
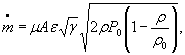
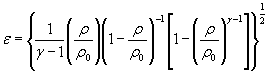
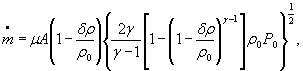
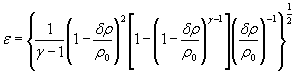
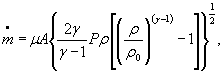
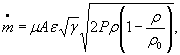
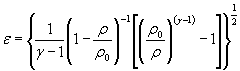
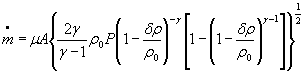
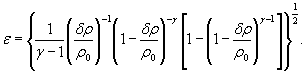
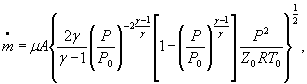
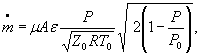
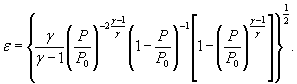
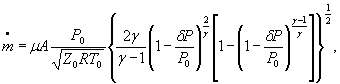
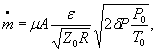
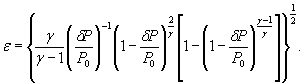
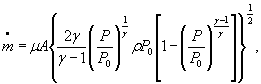
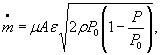
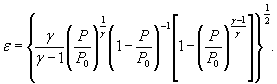
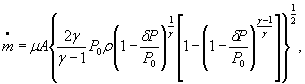
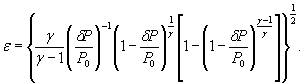
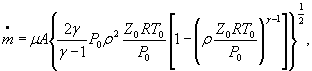
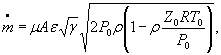
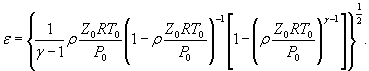
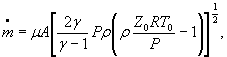
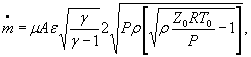
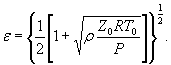
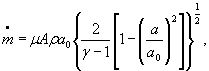
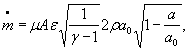
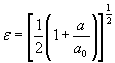 .
.