Краткие заметки о расчете железобетонных конструкций на действие изгибающих моментов и продольных сил
Краткие заметки о расчете железобетонных конструкций
на действие изгибающих моментов и
продольных сил
Москва
2008
В представленных заметках рассмотрен расчет железобетонных конструкций по нормальным сечениям на основе двухлинейной диаграммы «напряжения - деформации», объединяющий упругий, пластический и упругопластический расчеты железобетонных элементов.
Содержание
|
1. ОБЩИЕ СООБРАЖЕНИЯ 2. УРАВНЕНИЯ РАВНОВЕСИЯ 3. ДИАГРАММЫ СОСТОЯНИЯ БЕТОНА И АРМАТУРЫ 4. ХАРАКТЕР ДЕФОРМИРОВАНИЯ НОРМАЛЬНОГО СЕЧЕНИЯ ЖЕЛЕЗОБЕТОННОГО ЭЛЕМЕНТА 5. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ИСХОДЯ ИЗ НАКЛОННОГО УЧАСТКА ДИАГРАММ ДЕФОРМИРОВАНИЯ БЕТОНА И АРМАТУРЫ 6. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ИСХОДЯ ИЗ ГОРИЗОНТАЛЬНОГО УЧАСТКА ДИАГРАММ ДЕФОРМИРОВАНИЯ БЕТОНА И АРМАТУРЫ 7. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО НОРМАЛЬНЫМ СЕЧЕНИЯМ ИСХОДЯ ИЗ ПОЛНОЙ ДИАГРАММЫ ДЕФОРМИРОВАНИЯ БЕТОНА И АРМАТУРЫ 8. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕДСТАВЛЕННЫХ МЕТОДОВ РАСЧЕТА 9. РАСЧЕТ ДЕФОРМАТИВНОСТИ ИЗГИБАЕМЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ 10. ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
|
1. ОБЩИЕ СООБРАЖЕНИЯ
Разрушение железобетонных элементов при действии изгибающих моментов и продольных сил происходит в основном в результате образования нормальных трещин и последующего разрушения (раздробления) сжатой зоны бетона над нормальной трещиной или разрушения (разрыва) продольной растянутой арматуры, пересекающей нормальную трещину.
В соответствии с характером разрушения расчет железобетонных элементов на действие изгибающих моментов и продольных сил производится по нормальным сечениям, проходящим по нормальной трещине и бетону над ней.
Существует три основных метода расчета железобетонных элементов по нормальным сечениям: первый метод, применяемый ранее и именуемый как расчет по допускаемым напряжениям, второй метод, применяемый в последние годы и именуемый как расчет по предельным усилиям, и третий метод, применяемый в настоящее время и именуемый как расчет по деформационной модели. Все эти методы имеют существенные различия, однако представляется важным и полезным показать, что они основываются на общей характеристике деформирования бетона и арматуры - диаграммах деформирования, определяющих связь между напряжениями и деформациями бетона и арматуры.
2. УРАВНЕНИЯ РАВНОВЕСИЯ
Расчет железобетонных элементов по нормальным сечениям во всех случаях производится из уравнений равновесия моментов и продольных сил, действующих в нормальном сечении, от внешних нагрузок и от усилий в сжатой зоне бетона и растянутой арматуре.
Рассмотрим наиболее простой и типичный случай изгибаемого железобетонного элемента прямоугольного сечения с продольной арматурой, расположенной у растянутой грани элемента при действии изгибающего момента в плоскости симметрии нормального сечения (рис. 1).
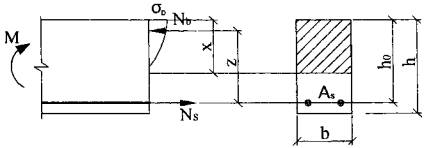
Рис. 1
Уравнения равновесия для нормального сечения запишутся в виде
M = N b z = N s z ;
Nb = N s
где Nb - усилие в сжатой зоне бетона 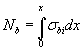 ;
;
σ bi - напряжения по высоте сжатой зоны;
Ns - усилие в растянутой продольной арматуре N s = σsAs ;
σ s - напряжения в растянутой продольной арматуре;
z - расстояние между точками приложения равнодействующих усилий в сжатой зоне бетона и растянутой продольной арматурой;
х - высота сжатой зоны.
Напряжения в бетоне и арматуре могут быть определены из диаграмм деформирования бетона и арматуры, связывающих напряжения с деформациями, и условия распределения деформаций по нормальному сечению.
3. ДИАГРАММЫ СОСТОЯНИЯ БЕТОНА И АРМАТУРЫ
Диаграммы состояния бетона и арматуры выражают связь между напряжениями и деформациями. Такие диаграммы могут быть получены из испытаний образцов бетона на осевое сжатие и образцов арматуры на осевое растяжение.
Диаграммы состояния бетона в целом имеют криволинейный характер с восходящим участком до максимальных значений напряжений и деформаций, а также и с нисходящим участком. Диаграммы состояния арматуры содержат линейный наклонный участок, затем линейный горизонтальный участок или криволинейный участок до максимальных значений напряжений и деформаций.
Для упрощения анализа криволинейные диаграммы целесообразно заменить двухлинейными, с первым, наклонным участком с некоторым углом наклона и вторым, горизонтальным участком, отвечающим предельным напряжениям и предельным деформациям бетона и арматуры (рис. 2 и рис. 3), так называемыми диаграммами Прандтля.
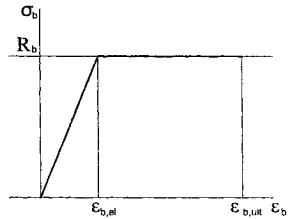
Рис. 2
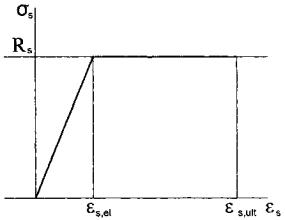
Рис.3
Если принимать во внимание только первый, наклонный участок диаграмм, то условия деформирования для бетона и арматуры запишутся в виде:
σ b = Eb,red·εb ≤ Rb;
σ s = Es·εs ≤ Rs,
где εb и εs - осевые деформации сжатого бетона и растянутой арматуры;
Eb , red - условный, приведенный модуль упругости сжатого бетона;
Es - физический модуль упругости растянутой арматуры;
Rb и Rs - расчетные сопротивления бетона осевому сжатию и арматуры осевому растяжению.
Если принять во внимание только второй, горизонтальный участок диаграмм, то условия деформирования для бетона и арматуры запишутся в виде:
σb = Rb; σs = Rs
т.е. напряжения в бетоне и арматуре равны расчетным сопротивлениям независимо от их деформаций.
Если принимать во внимание диаграммы деформирования бетона и арматуры, в целом состоящие из наклонного и горизонтального участков, то условие деформирования для бетона и арматуры запишется в виде:
при 0 ≤ εb ≤ εb , el ; σb = Eb , red εb ;
при εb 1 ≤ εb ≤ εb , ult ; σb = Rb ;
при 0 ≤ εs ≤ εs,el; σs = Es εs;
при εs1 ≤ εs ≤ εs,ult; σs = Rs,
где εs,ult и εb , ult предельные деформации бетона и арматуры;
εs,el и εb , el предельные упругие деформации бетона и арматуры.
Первая группа условий деформирования определяет условно упругую работу бетона и арматуры.
Вторая группа условий деформирования определяет условно пластическую работу бетона и арматуры.
Третья группа условий деформирования определяет условно упругопластическую работу бетона и арматуры.
Очевидно, для того чтобы использовать условия деформирования бетона и арматуры для определения напряжений в уравнениях равновесия, необходимо установить характер деформирования нормального сечения.
Двухлинейные диаграммы определяются двумя параметрическими точками: первой точкой, отвечающей границе упругой работы бетона и арматуры и характеризуемой напряжениями Rb и Rs и, соответственно, деформациями εb , el и εs,el и второй точкой, отвечающей предельному состоянию бетона и арматуры и характеризуемой напряжениями Rb и Rs и, соответственно, деформациями εb , ult и εs,ult.
Для бетона предельные деформации εb , ult определяются исходя из опытов на осевое сжатие и составляют примерно 0,002. Однако разрушение бетона у сжатой грани изгибаемых элементов наступает при больших значениях предельных деформаций в связи с имеющимся градиентом деформаций и напряжений по высоте сжатой зоны, которые могут быть приняты равными 0,0035.
Величина деформаций бетона εb , el , отвечающая границе его упругой работы, остается достаточно неопределенной. Она может быть принята исходя из начального модуля упругости бетона Еb , тогда εb , el = Rb / Eb . Она может быть принята равной некоторому среднему значению между εb , el = Rb / Eb и значению εb , el = εb , ult = 0,002, например εb , el = 0,0015. В этом случае приведенный модуль упругости бетона Eb , red будет равен Rb /0,0015. Далее для простоты мы будем рассматривать величину деформаций бетона εb , el определяемую через начальный модуль упругости бетона, то есть εb , el = Rb / Eb .
Естественно, все это относится к кратковременному действию нагрузки. При длительном действии нагрузки значения начального модуля упругости определяются с учетом коэффициента ползучести бетона и, соответственно, изменяются деформации бетона εb , el и εb , ult . Далее, приведенные параметры относятся к тяжелому бетону средней прочности. Для других видов бетона, а также для высокопрочных тяжелых бетонов деформационные параметры будут другими.
Для арматуры, обладающей четко выраженной площадкой текучести, величина деформаций εs , el , отвечающая границе ее упругой работы, определяется исходя из физического модуля упругости арматурной стали, то есть εs , el = Rs / Es . Что касается предельных деформаций арматуры εs , ult , то они, как правило, назначаются несколько меньше физических предельных деформаций, отвечающих разрыву арматуры, например 0,025, учитывая нецелесообразность развития больших пластических деформаций в арматуре.
Что касается арматуры, не имеющей выраженной площадки текучести, то для нее может быть, в принципе, применен такой же подход с двухлинейной диаграммой и определением граничных значений деформаций εs , el и εs , ult как и для арматуры, обладающей четко выраженной площадкой текучести, не учитывая в запас повышение напряжений сверх расчетных сопротивлений арматуры Rs , отвечающих условному пределу текучести и соответствующих остаточному относительному удлинению 0,02.
Следует также отметить, что, как показывают расчеты, конфигурация диаграмм при фиксированных параметрических точках не слишком влияет на конечные результаты расчета железобетонного элемента в целом.
4. ХАРАКТЕР ДЕФОРМИРОВАНИЯ НОРМАЛЬНОГО СЕЧЕНИЯ ЖЕЛЕЗОБЕТОННОГО ЭЛЕМЕНТА
При действии изгибающих моментов верхняя грань сжатого бетона получает деформации укорочения, а нижняя растянутая арматура получает деформации удлинения. Для простоты примем линейное распределение деформаций по высоте нормального сечения между крайними значениями деформаций сжатой зоны бетона и нижней растянутой арматурой, пересекающей нормальную трещину, известное как гипотеза плоских сечений, принимаемая в сопромате для сплошных элементов.
Очевидно, что деформирование железобетонного элемента с нормальными трещинами и арматурой, пересекающей эти трещины, может отличаться от деформирования сплошного элемента.
Имеется ряд предложений по более корректному назначению характера деформирования железобетонного элемента по нормальному сечению с трещинами. Тем не менее использование гипотезы плоских сечений для железобетонных элементов с трещинами позволяет существенно упростить расчет и получить общую методику, определяющую напряженно-деформированное состояние железобетонного элемента в целом (рис. 4).
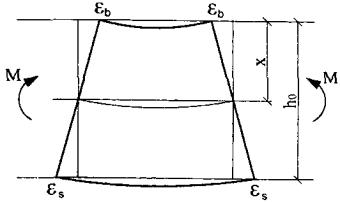
Рис. 4
Условие деформирования нормального сечения для приведенного выше изгибаемого железобетонного элемента запишется в виде:
![]()
где ε b - деформации вершины сжатой зоны бетона;
εs - деформации растянутой арматуры;
х - высота сжатой зоны бетона.
5. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ИСХОДЯ ИЗ НАКЛОННОГО УЧАСТКА ДИАГРАММ ДЕФОРМИРОВАНИЯ БЕТОНА И АРМАТУРЫ
Исходя из линейного распределения деформаций по нормальному сечению и диаграммы деформирования, по которой напряжения в бетоне и арматуре пропорциональны деформациям, можно заключить, что сжатая зона бетона имеет треугольную эпюру напряжений (рис. 5).
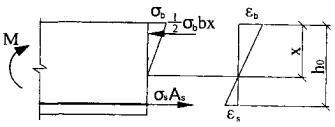
Рис. 5
В результате уравнение равновесия продольных сил для рассмотренных выше элементов запишется в виде:
![]()
где σ b - напряжения в вершине сжатой зоны бетона.
Выражая напряжения в бетоне сжатой зоны и в растянутой арматуре через деформации
σb = Eb εb , σs = Es εs ,
а соотношение между деформациями бетона и арматуры через линейную зависимость распределения деформаций по нормальному сечению
![]()
получим квадратное уравнение относительно высоты сжатой зоны х
х 2 = 2 αμsh 0 х - 2 αμsh 2 0 = 0,
из которого определяется высота сжатой зоны по формуле
![]()
здесь
α s = Es/Eb, μs = As/bh0.
Напряжения в вершине сжатой зоны бетона определяются по формуле, принимая момент относительно растянутой арматуры
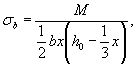
а напряжения в растянутой продольной арматуре определяются по формуле, принимая момент относительно равнодействующей усилий в сжатой зоне бетона
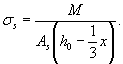
Предельный изгибающий момент, воспринимаемый нормальным сечением, при достижении напряжениями в вершине сжатой зоны расчетных сопротивлений бетона определяется по формуле
![]()
а предельный изгибающий момент, воспринимаемый нормальным сечением, при достижении напряжениями в продольной растянутой арматуре расчетных сопротивлений арматуры определяется по формуле
![]()
Очевидно, что предельные моменты при достижении предельного состояния по сжатому бетону и по растянутой арматуре имеют различные значения.
Граничную высоту сжатой зоны при одновременном достижении предельных деформаций в вершине сжатой зоны и в растянутой арматуре εb ,ult = Rb / Eb и εs ,ult = Rb / Eb можно определить исходя из условия деформирования нормального сечения
![]()
Подставляя значения εb ,ult и εs ,ult и делая соответствующие преобразования, получим выражение для граничной высоты сжатой зоны
![]()
Очевидно, при значениях высоты сжатой зоны больше граничных предельное состояние по бетону наступает раньше, чем по арматуре, при меньших значениях - наоборот.
Такую методику расчета железобетонных элементов, обозначаемую ранее как расчет по допускаемым напряжениям, можно квалифицировать как упругий расчет железобетонных элементов.
6. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ИСХОДЯ ИЗ ГОРИЗОНТАЛЬНОГО УЧАСТКА ДИАГРАММ ДЕФОРМИРОВАНИЯ БЕТОНА И АРМАТУРЫ
Исходя из диаграммы деформирования, по которой напряжения в бетоне и арматуре при любой величине деформаций равны расчетным сопротивлениям, получим прямоугольную эпюру напряжений в сжатой зоне бетона с напряжениями, равными расчетным сопротивлениям бетона сжатию, и напряжения в растянутой арматуре - равными расчетным сопротивлениям растяжению продольной арматуры (рис. 6).
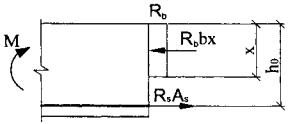
Рис. 6
В результате уравнение равновесия продольных сил в нормальном сечении для рассмотренных выше железобетонных элементов запишется в виде:
Rbbx = RsAs ,
откуда высота сжатой зоны определяется по формуле
![]()
или
![]()
Предельный момент, выраженный через предельные усилия в сжатой зоне бетона, определяется зависимостью
![]()
а предельный момент, выраженный через предельные усилия в растянутой арматуре, определяется зависимостью
![]()
Однако, как показано в предыдущем разделе, при разрушении по бетону напряжения в продольной растянутой арматуре могут не достигать расчетных сопротивлений арматуры растяжению Rs , а будут определяться из наклонного участка диаграммы. В этом случае граничная высота сжатой зоны, при которой напряжения в растянутой арматуре равны расчетным сопротивлениям растяжению, определяется из условия линейного распределения деформаций по нормальному сечению
![]()
принимая деформации в растянутой арматуре, соответствующие конечной точке наклонного участка диаграммы ε s , el = Rs / Es , а деформации в вершине сжатой зоны бетона - равные предельным значениям ε b = ε b , ult корректирующий коэффициент, учитывающий прямоугольную эпюру сжимающих напряжений в бетоне,
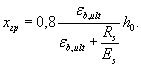
Таким образом, расчет, исходя из горизонтального участка диаграмм бетона и арматуры, принимая напряжения в бетоне и арматуре равными расчетным сопротивлениям, согласно приведенным формулам может производиться только при высоте сжатой зоны меньше граничной. При высоте сжатой зоны больше граничной расчет, очевидно, должен производиться, принимая для бетона горизонтальный участок диаграммы, а для арматуры - наклонный:
σb = Rb, σs = εsEs.
В этом случае высота сжатой зоны бетона определяется из уравнения равновесия продольных сил
Rbbx = σsAs ,
а напряжения в продольной арматуре получим из линейного распределения деформаций по нормальному сечению
![]()
и наклонного участка деформирования растянутой арматуры
σs = εsEs
при предельных деформациях вершины сжатой зоны бетона ε b = ε b , ult
![]()
В результате получаем квадратное уравнение относительно высоты сжатой зоны
х 2 + α 1 μs h 0 x - α 1 μs h 2 0 = 0,
где
![]()
из которого определяется высота сжатой зоны
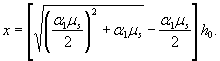
Таким образом, при х ≤ х гр предельный момент определяется по формуле
![]()
где
![]()
а при х > х гр предельный момент определяется по формуле
![]()
где
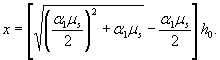
В запас прочности можно не рассматривать расчетную ситуацию при напряжениях в продольной арматуре меньших расчетных сопротивлений растяжению, а при х > х гр производить расчет, принимая напряжения в продольной растянутой арматуре равными расчетным сопротивлениям растяжению и х = х гр.
Представленный метод, обозначаемый как расчет по предельным усилиям, можно квалифицировать как пластический расчет железобетонных элементов.
7. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО НОРМАЛЬНЫМ СЕЧЕНИЯМ ИСХОДЯ ИЗ ПОЛНОЙ ДИАГРАММЫ ДЕФОРМИРОВАНИЯ БЕТОНА И АРМАТУРЫ
При расчете железобетонных элементов по нормальным сечениям, исходя из полной диаграммы деформирования бетона и арматуры, рассматриваются три расчетные ситуации.
Первая расчетная ситуация, когда деформации вершины сжатой зоны бетона и растянутой продольной арматуры находятся в пределах горизонтального участка диаграммы
εb , e l ≤ εb ≤ ε b , ult ;
εs , e l ≤ εs ≤ ε s , ult .
При этом напряжения в вершине сжатой зоны бетона равны расчетным сопротивлениям бетона сжатию Rb , а напряжения в растянутой арматуре - расчетным сопротивлениям арматуры растяжению Rs .
Вторая расчетная ситуация, когда деформации вершины сжатой зоны бетона находятся в пределах горизонтального участка диаграммы, а деформации растянутой продольной арматуры находятся в пределах наклонного участка диаграммы
εb, e l ≤ εb ≤ ε b, ult;
εs ≤ εs,el.
При этом напряжения в вершине сжатой зоны бетона равны расчетным сопротивлениям бетона сжатию Rb , а напряжения в растянутой продольной арматуре меньше или равны расчетным сопротивлениям арматуры растяжению.
Наконец, третья расчетная ситуация, когда деформации вершины сжатой зоны бетона находятся в пределах наклонного участка диаграммы, а деформации продольной растянутой арматуры находятся в пределах горизонтального участка диаграммы
εb ≤ εb,el;
εb,el ≤ εs ≤ ε s ,ult
При этом напряжения в вершине сжатой зоны бетона меньше или равны расчетным сопротивлениям бетона сжатию Rb , а напряжения в растянутой продольной арматуре равны расчетным сопротивлениям растяжению.
Первую расчетную ситуацию можно представить как разрушение по бетону при напряжениях в растянутой продольной арматуре, которые равны расчетному сопротивлению арматуры растяжению. Вторую расчетную ситуацию можно представить как разрушение по бетону при напряжениях в растянутой продольной арматуре, которые меньше расчетного сопротивления арматуры растяжению. Третью расчетную ситуацию можно представить как разрушение по арматуре при напряжениях в бетоне, которые меньше расчетного сопротивления бетона сжатию.
Для первой расчетной ситуации, исходя из линейного распределения деформаций по нормальному сечению, распределение напряжений по высоте сжатой зоны бетона должно быть адекватно двухлинейной диаграмме деформирования бетона. В результате мы имеем трапециевидную эпюру напряжений в сжатой зоне бетона, состоящую из прямоугольного участка высотой х 1 с напряжениями, равными расчетным сопротивлениям бетона сжатию Rb , и треугольного участка высотой х 2 с максимальными напряжениями в вершине этого участка, равными расчетным сопротивлениям бетона сжатию (рис. 7).
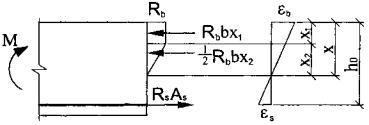
Рис.7
В этом случае уравнение равновесия продольных сил запишется в виде:
![]()
Соотношение между значениями х 1 и х 2 получаем из диаграммы деформирования бетона
![]()
или
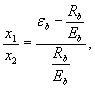
принимая
![]()
Значения параметров высоты сжатой зоны х 1 и х 2 определяются по формулам:
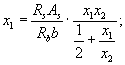
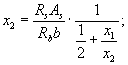
а общая высота сжатой зоны - по формуле
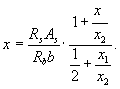
В результате предельный момент, воспринимаемый нормальным сечением, будет равен
![]()
при значениях х 1 и х 2 , определяемых, принимая ε b = ε b , ult т.е. деформации бетона в вершине сжатой зоны равны предельным значениям.
Для второй расчетной ситуации уравнение равновесия продольных сил запишется в виде:
![]()
или
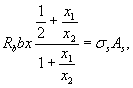
а напряжения в продольной арматуре определяются исходя из деформирования по наклонному участку диаграммы, условия линейного распределения деформаций по нормальному сечению и предельных деформаций бетона
![]()
В результате получим квадратное уравнение относительно высоты сжатой зоны
![]()
где
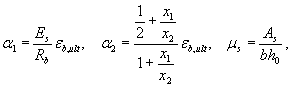
откуда
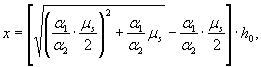
x 1 = α2 (1 + α2) x, x2 = (1 + α2) x
Предельный момент, воспринимаемый нормальным сечением, определяется по формуле
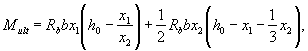
где x 1 и х2 определяются по полученным выше формулам.
Для третьей расчетной ситуации имеем треугольную эпюру напряжений в сжатой зоне бетона, и уравнение равновесия продольных сил запишется в виде:
![]()
а напряжения в вершине сжатой зоны бетона определяются из его деформирования по наклонному участку диаграммы, условия линейного распределения деформаций по нормальному сечению и предельных деформаций арматуры
![]()
В результате получим квадратное уравнение относительно сжатой зоны бетона
x 2 = α 3 μsh 0 x - α 3 μsh 2 0 = 0,
где
![]()
из которого определяется высота сжатой зоны
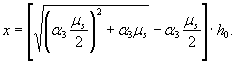
Отсюда предельный момент определяется по формуле
![]()
где высота сжатой зоны бетона х определяется по приведенной выше формуле.
Таким образом, мы получили три расчетные ситуации для определения предельного значения изгибающего момента.
Граничные состояния между этими расчетными ситуациями определяются величиной граничной высоты сжатой зоны бетона, которая устанавливается исходя из условия деформирования нормального сечения
![]()
и граничных значений деформации бетона и арматуры.
Для граничного состояния между первой и
второй расчетными ситуациями имеем ε b = ε b , ult и ![]() . В
результате граничная высота сжатой зоны бетона в этом случае равна
. В
результате граничная высота сжатой зоны бетона в этом случае равна
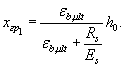
Для граничного состояния между первой и
третьей расчетными ситуациями имеем ![]() и ε s = ε s , ult . В результате граничная высота сжатой зоны бетона в
этом случае равна
и ε s = ε s , ult . В результате граничная высота сжатой зоны бетона в
этом случае равна
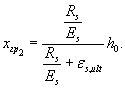
При расчете в качестве исходной, основной рассматривается первая расчетная ситуация, когда напряжения в вершине сжатой зоны и в растянутой арматуре равны расчетным сопротивлениям сжатия бетона и растяжения арматуры. В том случае, если полученная высота сжатой зоны бетона х оказывается больше первого граничного значения x гр 1 , расчет производится по второй расчетной ситуации при напряжениях в растянутой арматуре меньше расчетного сопротивления арматуры растяжению (х > x гр 1 ), и, если полученная высота сжатой зоны бетона х оказывается меньше второго граничного значения x гр 2 , то расчет производится по третьей расчетной ситуации при напряжениях в бетоне сжатой зоны меньше расчетного сопротивления бетона сжатию (х < x гр 2 ).
Представленный метод, обозначаемый как расчет по деформационной модели, можно квалифицировать как упругопластический расчет железобетонного элемента.
Заметим, что та или иная расчетная ситуация зависит от прочности бетона, прочности арматуры и относительного содержания продольной арматуры в нормальном сечении μ s = As / bh 0 (процента армирования). При средних значениях процента армирования реализуется первая расчетная ситуация, когда напряжения в бетоне и арматуре равны их расчетным сопротивлениям, при больших процентах армирования
реализуется вторая расчетная ситуация, когда напряжения в арматуре не достигают своих расчетных сопротивлений, а при малых процентах армирования реализуется третья расчетная ситуация, когда напряжения в бетоне не достигают своих расчетных сопротивлений.
8. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕДСТАВЛЕННЫХ МЕТОДОВ РАСЧЕТА
Расчет с использованием полной диаграммы деформирования бетона и арматуры наиболее универсален, так как он позволяет комплексно оценивать упругопластическую работу бетона и арматуры. Однако этот расчет приводит к более сложным и громоздким расчетным зависимостям.
Расчет с использованием только горизонтального участка диаграммы деформирования бетона и арматуры приводит к наиболее простым расчетным зависимостям. Его недостатком является учет только пластической работы бетона и арматуры, что требует введения дополнительных ограничений и корректив, когда бетон или арматура при разрушении элемента не достигают пластического состояния.
Расчет с использованием только наклонного участка диаграммы деформирования бетона и арматуры является наиболее осторожным, так как учитывает только упругую работу бетона и арматуры, тогда как на самом деле при разрушении элемента в бетоне и арматуре возникают и неупругие деформации. Упругий расчет железобетонных элементов обычно применяется в тех случаях, когда по тем или иным причинам желательно избежать развития неупругих, в том числе пластических, деформаций в бетоне и арматуре, в особенности на ранних стадиях работы железобетонных конструкций.
9. РАСЧЕТ ДЕФОРМАТИВНОСТИ ИЗГИБАЕМЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ
Кривизна изгибаемого железобетонного элемента определяется по формуле
![]()
где ε b - деформации бетона в вершине сжатой зоны;
εs - деформации растянутой арматуры.
Исходя из условия линейного распределения деформаций по нормальному сечению деформации растянутой арматуры можно выразить через деформации бетона
![]()
В результате кривизна изгибаемого железобетонного элемента выразится в виде
![]()
Рассматривая упругую работу бетона и арматуры (деформирование бетона и арматуры по наклонному участку диаграмм), деформации бетона выражаются через напряжения в виде
![]()
а напряжения в бетоне в вершине сжатой зоны - в виде
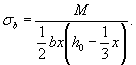
В результате кривизна изгибаемого железобетонного элемента определяется по формуле
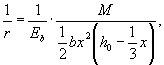
а изгибная жесткость железобетонного элемента как соотношение изгибающего момента и кривизны определяется по формуле
![]()
В приведенных выше формулах высота сжатой зоны бетона согласно приведенному выше анализу определяется по формуле
![]()
где
![]()
Рассматривая упругопластическую работу
бетона и арматуры (деформирование бетона и арматуры по горизонтальному участку
диаграмм), деформации бетона ε b , pl изменяются
от начала горизонтального участка до конца горизонтального участка ![]() . Кривизна изгибаемого железобетонного элемента определяется
по формуле
. Кривизна изгибаемого железобетонного элемента определяется
по формуле
![]()
Момент, соответствующий этому напряженному состоянию, определяется по формуле
![]()
где x , x 1 и х 2 определяются по формулам:
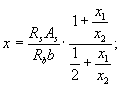
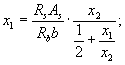
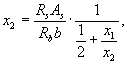
а соотношение между х 1 и x 2 определяется исходя из диаграмм по формуле
![]()
В результате изгибная жесткость железобетонного элемента как соотношение момента и кривизны определяется по формуле
![]()
Граничное значение кривизны и жесткости для горизонтального участка диаграммы бетона получается при ε b , pl = ε b , el и ε b , pl = ε b , ult . Исходя из этого может быть представлена диаграмма «момент-кривизна», которая описывает деформированное состояние железобетонного элемента в целом.
Упрощенно принимаем диаграмму «момент-кривизна» двухлинейной (рис. 8).
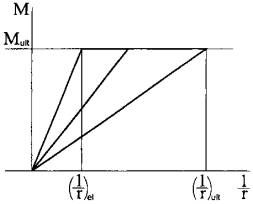
Рис. 8
Упругая жесткость железобетонных элементов с трещинами используется при расчете прогибов и ширины раскрытия трещин железобетонных конструкций для оценки пригодности конструкций и нормальной эксплуатации.
Пластическая жесткость железобетонных элементов с трещинами используется при оценке перераспределения усилий в железобетонных конструкциях, а также при учете жесткости железобетонных элементов в стадии, близкой к разрушению.
Общая схема напряженно-деформированного состояния железобетонного элемента с трещинами может быть представлена следующим образом.
При действии изгибающих моментов происходит плоский поворот нормальных сечений относительно нейтральной оси с образованием трещин в растянутой зоне и возникновением деформаций укорочения в сжатой зоне бетона и деформаций удлинения в продольной арматуре.
С увеличением изгибающего момента деформации укорочения сжатой зоны бетона и удлинения продольной арматуры увеличиваются с одновременным увеличением напряжений в сжатой зоне бетона и в растянутой арматуре в соответствии с диаграммами деформирования бетона и арматуры.
При деформациях, находящихся в зоне наклонного участка диаграмм, напряжения увеличиваются пропорционально увеличению деформаций.
Далее, при увеличении изгибающего момента деформации в вершине сжатой зоны бетона либо в растянутой арматуре достигают граничной точки между наклонными и горизонтальными участками диаграмм и затем при дальнейшем увеличении изгибающего момента и, соответственно, деформаций напряжения в бетоне и арматуре, следуя горизонтальному участку по диаграмме деформирования, остаются постоянными и равными расчетным сопротивлениям бетона и арматуры.
Разрушение элемента фиксируется, когда деформации в вершине сжатой зоны бетона либо растянутой арматуре достигают предельных значений. Полученное напряженно-деформированное состояние сжатой зоны бетона и растянутой арматуры определяет предельную величину изгибающего момента, которую может воспринять нормальное сечение.
В диаграмме «момент-кривизна» жесткость
элемента, определяемая как соотношение ![]() , характеризуется наклонной линией, следующей к
рассматриваемой точке диаграммы. При упругой работе железобетонного элемента
жесткости имеют постоянные и наибольшие значения.
, характеризуется наклонной линией, следующей к
рассматриваемой точке диаграммы. При упругой работе железобетонного элемента
жесткости имеют постоянные и наибольшие значения.
При переходе в пластическое деформирование жесткость элемента уменьшается и получает наименьшие значения при максимальной кривизне, характеризуемой предельными деформациями вершины сжатой зоны либо растянутой арматуры.
10. ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Выше был рассмотрен наиболее простой, но типичный изгибаемый железобетонный элемент прямоугольного сечения с продольной арматурой, расположенной у растянутой грани элемента. Очевидно, подобный диаграммный анализ может быть применен к железобетонным элементам и другой конфигурации (тавровым, круглым, кольцевым), с арматурой, распределенной по высоте сечения, а также к внецентренно сжатым и внецентренно растянутым элементам, при косом изгибе, косом внецентренном сжатии и косом внецентренном растяжении. Однако в этих случаях расчет в значительной степени усложняется и приходится переходить на компьютерные программы. Поэтому нами был выбран наиболее простой пример, на котором наиболее отчетливо можно было продемонстрировать влияние диаграммы деформирования на расчет железобетонного элемента.