РД 51-4.2.-003-97 Методические рекомендации по расчетам конструктивной надежности магистральных газопроводов

РОССИЙСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО "ГАЗПРОМ"
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАСЧЕТАМ КОНСТРУКТИВНОЙ НАДЕЖНОСТИ
МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ
РД 51-4.2.-003-97
Москва 1997
Российское акционерное общество "Газпром"
Ассоциация "Высоконадежный трубопроводный транспорт"
ВНИИГАЗ
Информационно-рекламный
центр газовой промышленности
(ИРЦ Газпром)
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РАСЧЕТАМ КОНСТРУКТИВНОЙ НАДЕЖНОСТИ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ
РД 51-4.2.-003-97
Москва 1997
Настоящие "Методические рекомендации по расчетам конструктивной надежности магистральных газопроводов" составлены в соответствии со СНиП 10-01-94 "Система нормативных документов в строительстве. Основные положения" и ГОСТ 27.002-89 "Надежность в технике. Основные понятия. Термины и определения". В "Методических рекомендациях..." изложены основные положения и расчетные методы конструктивной надежности линейной части магистральных газопроводов, представлены алгоритмы и программные комплексы по прогнозированию показателей надежности, основанные на математических методах конструктивной надежности, критериях предельных состояний, оценках напряженно-деформированного состояния участков газопроводов. В Приложениях к "Методическим рекомендациям..." изложены практические примеры количественного определения параметров надежности на стадии проектирования и в процессе эксплуатации.
"Методические рекомендации..." обсуждены на секции по надежности и ресурсу Ученого совета ВНИИгаза, научном семинаре ИМАШ РАН, координационном совете межгосударственной программы "Высоконадежный трубопроводный транспорт".
"Методические рекомендации...", доработанные с учетом замечаний отраслевых проектных институтов, были рассмотрены на расширенном техническом совещании в Управлении проектно-изыскательских работ и экспертизы проектов РАО "Газпром" и рекомендованы к практическому внедрению в отрасли.
"Методические рекомендации..." предназначены для отраслевых исследовательских и проектных организаций, инженерных служб газотранспортных предприятий и специализированных организаций, выполняющих диагностические работы на магистральных газопроводах.
Разработчики: д.т.н. Харионовский В.В. (руководитель), к.т.н. Курганова И.Н., инж. Широков М.А. (ВНИИгаз, РАО "Газпром"), к.т.н. Силкин В.М., к.т.н. Нефедов С.В. (ИМАШ РАН), д.т.н., проф. Иванцов О.М. (АО Роснефтегазстрой), д.т.н. Завойчинский Б.И. (ВНИИСТ)
Под редакцией: акад. Патона Б.Е., к.т.н. Динкова В.А., д.т.н., проф. Иванцова О.М.
Официальный рецензент: акад. РАН Болотин В.В.
Согласованы с Управлением проектно-изыскательских работ и экспертизы проектов, Управлением научно-технического прогресса и экологии. Управлением по транспортировке газа и газового конденсата, Управлением газового надзора.
Подготовлены к утверждению Управлением проектно-изыскательских работ и экспертизы проектов РАО "Газпром".
Утверждены заместителем Председателя Правления РАО "Газпром" В.В. Ремизовым 3 апреля 1997 г.
Введены в действие с 1 июня 1997 г. Приказам РАО "Газпром" от 24 апреля 1997 г., № 55.
1. НАЗНАЧЕНИЕ, СТРУКТУРА И ОБЛАСТЬ ПРИМЕНЕНИЯ
Расчет сроков службы газопровода, выполненный в соответствии с Методическими рекомендациями, призван обеспечить оптимальность выбора его конструктивной схемы при требуемом уровне эксплуатационной надежности и безопасности.
1.1. Технико-экономическая постановка задачи
Постановка задачи подчиняется общей схеме 1 и включает оценку проекта с точки зрения технико-экономических требований к производительности и эффективности проектируемой трубопроводной магистрали. Включают назначаемые показатели экономической эффективности, мощности транспортной сети по перекачке газа, допустимые предельные значения потерь продукта, технико-экономические показатели капиталовложений на проектирование, изготовление комплектующих и материалов, доставку, строительство, номинальные условия эксплуатации, потери на поддержание ресурса за весь прогнозируемый период эксплуатации и т.п.
Основным документом по надежности является терминологический стандарт ГОСТ 27.002-89 "Надежность в технике. Основные понятия, термины и определения".
1.2. Структура Методических рекомендаций
Структура настоящих Методических рекомендаций соответствует современным международным нормам стандартизации в области надежности и безопасности технических объектов и систем, правилам и нормам проектирования строительных конструкций и правилам по расчетам показателей прочности, надежности и долговечности трубопроводов международных организаций по стандартизации в данной области.
Структура Методических рекомендаций основана на полном адекватном описании объекта и включает следующие позиции:
- предназначение проектируемого объекта;
- структурные и конструктивные особенности объекта;
- прогнозируемые испытываемые нагрузки и воздействия окружающей среды;
- классификация возможных типов отказов;
- выбор предельных состояний и формализация критериев предельных состояний для соответствующих типов отказов;
- формирование расчетных участков и требований к расчетным схемам участков и конструктивных элементов;
- выбор и определение показателей надежности, долговечности и безопасности;
- методы прогнозирования показателей;
- требования к исходной информации.

Рис. 1.1
2. ОСНОВЫ СТАНДАРТИЗАЦИИ И НОРМИРОВАНИЯ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ
2.1. Основные понятия
Надежность - свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции. Надежность - комплексное свойство, состоящее в общем случае из безотказности, долговечности, ремонтопригодности и сохраняемости.
Безотказностью называют свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени наработки. Под долговечностью понимают способность объекта не достигать в течение достаточно длительного времени предельного состояния, т.е. такого, при котором дальнейшее использование объекта по назначению становится невозможным или нецелесообразным, несмотря на наличие установленной системы технического обслуживания и ремонта. Объект может перейти в предельное состояние, оставаясь работоспособным, если его дальнейшее применение станет недопустимым по требованиям безопасности, экономичности или эффективности. Ремонтопригодность - это свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта.
Безопасность - свойство объекта при изготовлении и эксплуатации и в случае нарушения работоспособного состояния не создавать угрозу для населения и/или для окружающей среды. Под живучестью понимаем свойство объекта, состоящее в его способности противостоять развитию критических и существенных отказов из дефектов, повреждений и несущественных отказов при установленной системе технического обслуживания и ремонта. Примером служит сохранение несущей способности линейных частей магистральных газопроводов при возникновении в них усталостных трещин, размеры которых не превышают заданных значений.
Состояние объекта, при котором он соответствует всем требованиям документации, называют исправным. Если объект не соответствует хотя бы одному из требований, то его состояние называют неисправным. Состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям документации, называют работоспособным.
Если значение хотя бы одного параметра, характеризующего способность объекта выполнять заданные функции, не соответствует указанным требованиям, то состояние называют неработоспособным. В общем случае вводится промежуточное понятие частично неработоспособного (частично работоспособного) состояния. Примером частично неработоспособного состояния служит такое состояние ЛЧМГ, при котором участок способен выполнять требуемые функции по перекачке газоконденсата с пониженными показателями, в частности, с пониженной производительностью (при более низком давлении, чем номинальное).
Переход объекта в предельное состояние влечет за собой временное или окончательное прекращение эксплуатации объекта. При достижении предельного состояния объект должен быть снят с эксплуатации, направлен в средний или капитальный ремонт, списан, уничтожен или передан для применения не по назначению. Для ремонтируемых объектов выделяют два или более видов предельных состояний. В одних случаях требуется отправка объекта в средний или капитальный ремонт, в других случаях предельное состояние влечет за собой окончательное прекращение применения объекта по назначению.
Под отказом понимают любое событие, заключающееся в нарушении работоспособного состояния объекта. Отказ может быть полным, когда в результате отказа наступает полное неработоспособное состояние объекта, и частичным, когда наступает частично неработоспособное состояние. Совокупность признаков нарушения работоспособного состояния объекта устанавливают в нормативно-технической или проектно-конструкторской документации (далее для краткости - в документации). Необходимо отличать отказы от повреждений, т.е. от нарушений исправного состояния объекта при сохранении его работоспособного состояния.
Классификация отказов по последствиям необходима при нормировании надежности, в частности, для обоснования выбора номенклатуры и численных значений нормируемых показателей надежности.
Среди всех отказов выделяют особо опасные - катастрофические отказы, наступление которых создает угрозу для жизни и здоровья людей, а также для окружающей среды, или приводит к тяжелым экономическим потерям. К критическим отказам относятся такие, возникновение которых приводит к невыполнению ответственного задания. Отнесение отказа к той или иной категории является предметом соглашения между заказчиком (потребителем) и разработчиком (изготовителем).
Наработка до отказа характеризует продолжительность эксплуатации объекта от ее начала до возникновения отказа. Наработку между отказами отсчитывают от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа.
Долговечность объекта характеризуют его ресурсом или сроком службы. Техническим ресурсом (или просто - ресурсом) называют суммарную наработку объекта от начала его эксплуатации или ее возобновления после ремонта до перехода объекта в предельное состояние. Срок службы определяют как календарную продолжительность эксплуатации объекта от ее начала или возобновления после ремонта до перехода объекта в предельное состояние.
2.2. Показатели надежности
Показателями надежности называют количественные характеристики одного или нескольких свойств, составляющих надежность объекта. В первом случае показатели называют единичными, во втором - комплексными. Показатели надежности относятся к числу важнейших понятий статистической теории надежности / 1, 2, 5, 6/.
На стадии проектирования и конструирования показатели надежности трактуют как характеристики вероятностных или полувероятностных математических моделей создаваемых объектов. Соответствующие значения показателей называют расчетными. Аналогичные оценки по данным эксплуатации называют эксплуатационными. В нашей стране номенклатуру показателей надежности регламентирует стандарт / 3/. Хотя с учетом специфики отрасли допускается использование показателей, не включенных в этот стандарт, эти показатели не должны противоречить понятиям, лежащим в основе стандарта.
В целях единообразия все показатели надежности, перечисленные в стандарте / 3/, определены как вероятностные характеристики.
Основной показатель безотказности - вероятность безотказной работы, т. е. вероятность того, что в пределах заданной наработки не возникнет ни одного отказа. Вероятность безотказной работы на отрезке [0, t ] определяют по формуле:
P(t)=P{ t >t}, (2.1)
где t - наработка на первый отказ;
t - суммарная наработка.
Вероятность безотказной работы Р (t) связана с функцией распределения F ( t ) и плотностью распределения f ( t ) наработки до отказа:
F ( t ) = 1 - P ( t ), f ( t ) = dF ( t )/ dt = - dP ( t )/ dt . (2.2)
Наряду с понятием "вероятность безотказной работы" часто используют понятие "вероятность отказа", которое определяют следующим образом: это вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени. Вероятность наступления хотя бы одного отказа на отрезке [0, t ] определяют по формуле
Q(t)=1 - P(t)=F(t) (2.3)
Для высоконадежных объектов вероятность безотказной работы по отношению к критическим (тем более - катастрофическим) отказам должна быть весьма близка к единице. Вероятность наступления хотя бы одного критического отказа на заданном отрезке времени обычно называют показателем риска или просто риском.
Интенсивность отказов - это плотность вероятности возникновения отказа, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Интенсивность отказов ( t ) выражают через функции P ( t ), F ( t ) и f ( t ) следующим образом:
![]() (2.4)
(2.4)
Для высоконадежных систем P ( t ) » 1, так что интенсивность отказов приближенно равна плотности распределения f ( t ) наработки до отказа.
Перечисленные показатели введены применительно к невосстанавливаемым объектам, а также к таким отказам восстанавливаемых объектов, возникновение которых по возможности должно быть исключено. Применительно к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы, вместо средней наработки до отказа используют показатель - среднюю наработку на отказ. Очевидно, что это должны быть несущественные отказы, не приводящие к серьезным последствиям и не требующие значительных затрат на восстановление работоспособного состояния.
Эксплуатация восстанавливаемых объектов может быть описана следующим образом: в начальный момент времени объект начинает работать и продолжает работать до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д. На оси времени t моменты отказов образуют поток отказов, а моменты восстановлении - поток восстановлении. На оси суммарной наработки (когда продолжительность восстановления не учитывают) моменты отказов образуют поток отказов. Полное и строгое математическое описание эксплуатации объекта, по этой схеме построено на основе теории восстановления / 1/.
Средняя наработка на отказ определяется по формуле
![]() (2.5)
(2.5)
Здесь t - суммарная наработка, r ( t ) - число отказов, наступивших в течение этой наработки, М{ } - математическое ожидание случайной величины, стоящей в скобках. В общем случае средняя наработка на отказ - функция t. Для стационарных потоков отказов средняя наработка на отказ от t не зависит.
Для восстанавливаемых объектов используют еще один показатель - параметр потоков отказов, равный отношению математического ожидания числа отказов за достаточно малую наработку объекта к значению этой наработки.
Большинство показателей долговечности аналогично показателям безотказности невосстанавливаемых объектов, если в определениях момент наступления первого отказа заменить на момент достижения предельного состояния. Например, гамма-процентный ресурс определяют как суммарную наработку, в течение которой в заданных режимах и условиях применения объект не достигает предельного состояния с вероятностью у, выраженной в процентах. Аналогично вводят гамма-процентный срок службы как календарную продолжительность эксплуатации, в течение которой объект не достигает предельного состояния с выраженной в процентах вероятностью у. Применительно к крупносерийным объектам и массовым комплектующим изделиям обычно используют понятие среднего ресурса и среднего срока службы. В терминах вероятностных моделей эти показатели равны математическим ожиданиям суммарной наработки и календарной продолжительности до достижения предельного состояния.
Необходимо различать показатели долговечности от внешне сходных с ним "назначенных" сроков службы. Цель установления назначенного срока службы и назначенного ресурса - обеспечить принудительное и заблаговременное прекращение применения объекта по назначению из требований безопасности или технико-экономических соображений. При достижении объектом назначенного ресурса (назначенного срока службы, назначенного срока хранения) в зависимости от назначения объекта, особенности его эксплуатации, технического состояния и других факторов объект может быть списан, направлен в средний или капитальный ремонт, передан для применения не по назначению и т.д. При определенных условиях после обследования может быть принято решение о продолжении эксплуатации. Назначенный срок службы, назначенный ресурс являются технико-эксплуатационными характеристиками. Однако при установлении их численных значений следует принимать во внимание прогнозируемый или достигнутый уровень надежности. В частности, если поставлено требование безопасности, то назначенный срок службы (ресурс) должен отвечать значениям вероятности безотказной работы по отношению к критическим отказам, весьма близким к единице.
Различают две группы показателей ремонтопригодности. Первая группа аналогична показателям безотказности типа вводимых формулами ( 2.1) - ( 2.5). К ним относится вероятность восстановления, т.е. вероятность того, что продолжительность восстановления работоспособного состояния объекта не превысит заданное значение. Квантили этой вероятности - продолжительность времени, в течение которого восстановление работоспособности будет осуществлено с вероятностью g , выраженной в процентах, называют гамма-процентным временем восстановления. Аналогично вводят среднее время восстановления, интенсивность восстановления и параметр потока восстановления. Другая группа показателей ремонтопригодности характеризует трудовые затраты по поддержанию работоспособного состояния объекта. К ним относят среднюю трудоемкость восстановления, которую обычно измеряют в человеко-часах. Большинство показателей этого типа - численные характеристики трудоемкости технического обслуживания, ремонта, диагностирования и т.п., строго говоря, не относятся к показателям надежности.
2.3. Применение моделей и методов теории надежности при проектировании ЛЧМГ
Расчет линейных частей трубопроводов до сих пор проводят, в том числе и в промышленно развитых странах, на основе традиционных методов строительной механики с использованием концепции коэффициентов запаса. При этом не может быть в полной мере учтено разнообразие условий эксплуатации трубопровода, сочетание различных факторов, статистический разброс механических свойств материала, параметров формы, начальная дефектность трубопровода. В ряде случаев, как например, при анализе взаимодействия трубопровода с промерзающим грунтом в условиях морозного пучения, вследствие недостатка информации о действительных условиях эксплуатации и свойствах грунта, информация о них будет изначально носить статистический характер. Указанные обстоятельства обусловливают повышение удельного веса вероятностных моделей при расчете трубопроводов.
Оценка надежности всей газопроводной системы подразумевает выделение однородных групп элементов системы (компрессорные станции, линейные части магистральных газопроводов и т.д.) с последующим анализом отказов подсистем. Здесь применяется методология системной теории надежности, которая применительно к магистральным газопроводам подразумевает несколько уровней разукрупнения системы . Будем рассматривать уровень, для которого объектом исследования является линейная часть магистрального газопровода. На этом уровне выделяются следующие подсистемы: 1) группа А - основной металл (трубы) со сварными соединениями (сварные швы) и конструктивными особенностями типа ветвлений, отводов, тройников и т. п., 2) группа В - элементы конструктивной оснастки, включающей средства электрохимзащиты, прокладки (свайное основание, способ грунтовой засыпки и т. п.), антикоррозионные покрытия и т.п. Надежность всей системы в целом (на данном уровне разукрупнения) зависит от надежности составляющих ее компонент (выделенных подсистем). Между отказами групп А и В существует очевидная статистическая зависимость, которая предполагает применение для оценки показателей безотказности методов условных функций надежности / 2/. Такой приближенный подход определяется отсутствием полной информации о распределениях условных вероятностей отказов в группе А при отказе в группе В.
С другой стороны, при рассмотрении конструктивной схемы конкретной газопроводной системы необходимо провести структурный анализ, при котором газопровод рассматривается как протяженная механическая система, состоящая из однородных по способу прокладки, грунтово-геологическим, климатическим и эксплуатационным условиям участков. Выделение однородных участков осуществляется в соответствии с принципом равной надежности. Для выделенной группы участков характерны отказы, имеющие одинаковую природу (причина отказа описывается одним и тем же критерием наступления предельного состояния).
Третий момент классификации предусматривает изучение физико-механической природы возможных отказов выделенных участков по группам оборудования газопровода А и В. При этом обращается внимание на причину отказа, степень критичности (несущественный, существенный, критический), возможности восстановления работоспособности конструктивных элементов после отказа. Последнее предполагает выделение резервируемых участков, а, следовательно, применение для прогнозирования показателей безотказности методов теории надежности систем с резервированием / 1/.
Последовательные этапы разукрупнения системы и отдельные элементы конструктивной расчетной схемы проиллюстрированы на рис. 2.1. Надежность ЛЧМГ длиной L за период эксплуатации Т с учетом разбиения на N групп однородных участков может быть оценена по формуле
![]() ,
(2.6)
,
(2.6)
где D L , - суммарная протяженность i-ой однородной группы. Здесь учтено предположение о независимости отказов на каждом из выделенных участков. Надежности групп участков Ri ( D Li , T ) определяются в соответствии с принятой номенклатурой возможных отказов (вообще говоря, специфических для каждого из участков группы). С точки зрения подсистем А и В надежность Ri ( D Li , T ) определяется соотношением
![]() , (2.7)
, (2.7)
где
векторы качества ![]() и
и ![]() представляют
совокупности независимых управляющих параметров i-ой группы участков
соответственно по конструктивным подсистемам А и В;
представляют
совокупности независимых управляющих параметров i-ой группы участков
соответственно по конструктивным подсистемам А и В; ![]() и
и ![]() представляют собой
допустимые области в пространстве качества векторов
представляют собой
допустимые области в пространстве качества векторов ![]() и
и ![]() соответственно. Формула (2.7) выражает тот факт,
что вероятность отказа системы рассматриваемого уровня определяется
вероятностью отказа основного металла или сварных соединений при условии
возникновения события отказа группы В (например, выход из строя свайного
основания может привести к критической просадке участка надземного газопровода,
неустановившимся колебаниям, контактному ударному взаимодействию с просевшей
опорой с последующим разрывом оболочки трубы или ее разгерметизацией). Для
вычисления вероятностей ( 2.7)
в условиях неполной информации применимы методы условных функций надежности / 2/. При этом главную
задачу составляет определение вероятности безотказной работы группы А -
основного металла и сварных соединений трубопровода, отказы которой могут
привести к утечкам с катастрофическими последствиями.
соответственно. Формула (2.7) выражает тот факт,
что вероятность отказа системы рассматриваемого уровня определяется
вероятностью отказа основного металла или сварных соединений при условии
возникновения события отказа группы В (например, выход из строя свайного
основания может привести к критической просадке участка надземного газопровода,
неустановившимся колебаниям, контактному ударному взаимодействию с просевшей
опорой с последующим разрывом оболочки трубы или ее разгерметизацией). Для
вычисления вероятностей ( 2.7)
в условиях неполной информации применимы методы условных функций надежности / 2/. При этом главную
задачу составляет определение вероятности безотказной работы группы А -
основного металла и сварных соединений трубопровода, отказы которой могут
привести к утечкам с катастрофическими последствиями.
На рис. 2.1 представлена общая схема, иллюстрирующая последовательность прогнозирования работоспособного состояния отдельного участка ЛЧМГ с учетом возможного наличия в нем геометрических несовершенств и дефектов, а также с учетом возникновения вторичных дефектов. Управление в горизонтальных слоях схемы (основной металл - дефект - вторичный дефект) осуществляется средствами расчетно-экспериментальных методов оценки напряженно-деформированного состояния оболочки с геометрическими несовершенствами в структуре, концентраторами напряжений, трещинами и т.п.
Последовательность прогнозирования показателей надежности участка ЛЧМГ в соответствии с предложенной схемой представляется следующей:
1. На уровне методологического обеспечения необходимы:
- классификатор возможных (наблюдаемых в аналогах) дефектов и геометрических несовершенств;
- наличие статистической информации о типе и уровне нагрузок и воздействий в районе эксплуатации будущего объекта;
- выбор, разработка и применение расчетных методов оценки напряженно-деформированного состояния конструктивных элементов ЛЧМГ с дефектами и геометрическими несовершенствами;
- накопленная диагностическая информация об аналогичных дефектах.
2. Основной металл и сварные соединения:
2.1. Определяется напряженно-деформированное состояние;
2.2. Проверяются условия прочности и упругой устойчивости для оценки выполнения критериев ненаступления предельного состояния по основному конструктивному элементу без учета геометрических несовершенств и дефектов;
2.3. В случае наступления предельного состояния информация об этом факте поступает в блок оценки показателей надежности;
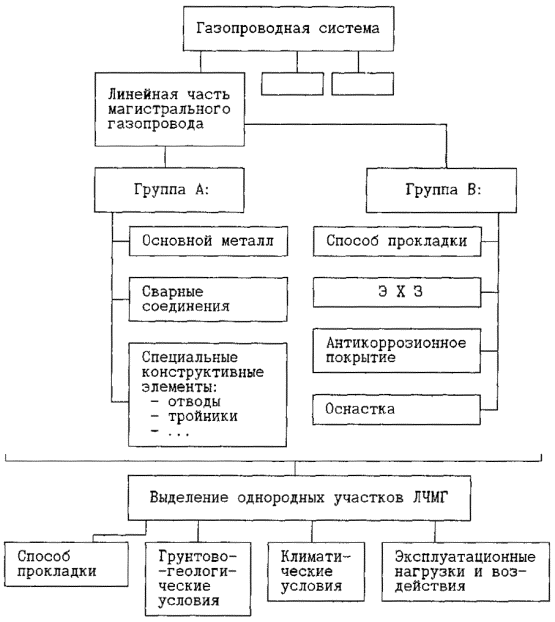
Рис. 2.1.
2.4. В случае ненаступления предельного состояния исследуются геометрические несовершенства;
3. Для выделенных по данным диагностической информации типов дефектов (для конкретного исследуемого участка трубопровода) последовательно по каждому из дефектов (несовершенств) проводится следующий анализ:
3.1. Определяется напряженно-деформированное состояние в области концентратора (несовершенства) с учетом НДС основного металла (сварного шва);
3.2. Исследуется выполнение условий прочности и устойчивости для области концентратора (несовершенства);
3.3. Исследуется вопрос о наступлении предельного состояния для участка ЛЧМГ при нарушении критериев п. 3.2;
3.4. В случае наступления предельного состояния информация об этом факте поступает в блок оценки показателей надежности;
3.5. В случае ненаступления предельного состояния осуществляется исследование дефектов с точки зрения механики разрушения;
3.6. Исследуется выполнение условий трещиностойкости (для трещиноподобных дефектов);
3.7. Исследуется вопрос о наступлении предельного состояния для участка ЛЧМГ при нарушении критериев трещиностойкости п. 3.6;
3.8. В случае наступления предельного состояния информация об этом факте поступает в блок оценки показателей надежности;
3.9. В случае ненаступления предельного состояния осуществляется исследование возможности образования вторичных дефектов;
3.10. При наличии вторичных дефектов на момент исследования (из диагностической информации) переходим к их исследованию;
3.11. При отсутствии диагностической информации о наличии вторичных дефектов исследуется возможность их появления при выполнении критериев образования вторичных дефектов;
3.12. В случае возникновения вторичных дефектов при исследовании по п. 3.11. переходим к их исследованию;
3.13. В случае невыполнения условий образования вторичных дефектов переходим к исследованию уже имеющихся в наличии.
4. Исследование вторичных дефектов подразумевает, что сформированы критерии наступления предельного состояния для участка ЛЧМГ в случае нарушений критериев трещиностойкости для вторичных дефектов;
4.1. Исследуется напряженно-деформированное состояние НДС для зоны вторичных дефектов;
4.2. Исследуется выполнение критериев трещиностойкости для вторичных трещиноподобных дефектов (или иных критериев надежности и безопасности при вторичных дефектах иной природы - питтинговая коррозия, например);
4.3. Исследуется вопрос о наступлении предельного состояния для участка ЛЧМГ при нарушении критериев трещиностойкости п. 4.2;
4.4. При любом исходе информация о результатах поступает в блок оценки вероятностных показателей надежности и безопасности;
4.5. Исследование по представленным п. п. 2- 4 продолжается для всех типов дефектов;
5. Выполняется оценка показателей надежности и безопасности.
6. В случае удовлетворения полученной оценки назначаемым значениям (по требованиям заказчика и т.п.) технический проект направляется в конструкторскую проработку. В противном случае необходимы дополнительные технические решения на уровне создания исходного проекта и повторение процедур оценки по п. п. 1- 5.
В комментарии к схеме отметим, что она не подразумевает жесткого выполнения указанной последовательности. Возможны ситуации, когда исследование надежности может ограничиться только отдельными пунктами. С другой стороны, для возможных сложных повреждений часто необходимо решение всей перечисленной последовательности задач: от исследования прочности и устойчивости основного конструктивного элемента до оценки трещиностойкости задира, например, в области вмятины. Комплексность подхода не означает, что взаимовлиянием повреждений и дефектов можно пренебречь. Этот вопрос должен специально решаться на соответствующих этапах определения напряженно-деформированного состояния (при выборе расчетной схемы). При этом необходимо оговаривать и обосновывать предположения о невзаимовлиянии НДС отдельных дефектов. Принципиальная схема прогнозирования надежности трубопроводов с дефектами дана на рис. 2.2.
Предложенная методология распространима практически на любые виды дефектов. Специфика конкретных задач будет заключаться исключительно в определении количественных закономерностей предельного состояния и вычисления по соответствующей физической модели вида и параметров функции распределения F ( t ).
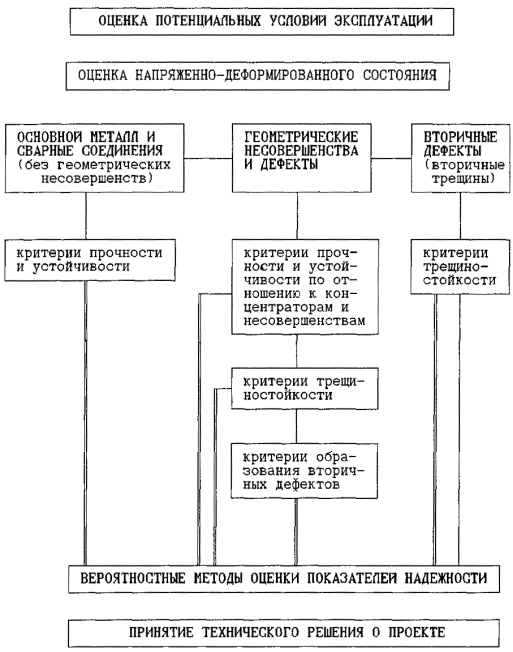
Рис. 2.2. Схема прогнозирования надежности и безопасности трубопроводов с дефектами
3. МЕТОДИКА РАСЧЕТА ПОКАЗАТЕЛЕЙ КОНСТРУКТИВНОЙ НАДЕЖНОСТИ ЛИНЕЙНЫХ ЧАСТЕЙ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ
3.1. Осно вные характеристики конструкции ЛЧМГ и трассы газопровода в целом
3.1.1. К линейной части магистрального газопровода (ЛЧМГ) относятся собственно трубопровод с линейной арматурой, переходами через естественные и искусственные преграды, линии технологической связи и электропередачи, вдольтрассовые и подъездные дороги, защитные сооружения и т.п. В дальнейшем под ЛЧМГ мы будем понимать только трубопровод (нитка из цельнотянутых, сварных (прямошовных и спиральношовных труб) с антикоррозионным покрытием) и свайное основание для надземных систем.
3.1.2. В качестве элементов технологической части магистрального газопровода следует рассматривать отдельные элементы конструкции:
- узлы пуска и приема очистных устройств;
- газопровод, проходящий по территории КС и внутри ее зданий и сооружений;
- всасывающий коллектор обвязочного газопровода КС;
- нагнетательный коллектор обвязочного газопровода КС;
- газопровод, примыкающий к ГРС и СПХГ;
- подводные переходы.
3.1.3. К основным характеристикам конструкции ЛЧМГ относятся следующие группы данных:
3. 1.3. 1. Конструктивная схема прокладки трубопровода;
3.1.3.2. Координаты, определяющие ориентацию продольной оси трубопровода на всем протяжении трассы;
3.1.3.3. Основные пространственные характеристики конструктивных элементов с указанием допускаемых отклонений от номинальных размеров, включая искажения формы изделий (номинальный наружный D н и внутренний D вн диаметры труб, толщина стенки h , допускаемый нормативный разброс этих значений, допускаемое отклонение поперечного сечения трубы от круговой формы, геометрические характеристики формы сварных швов и т.п.).
3.1.3.4. Физико-механические, включая прочностные, свойства применяемых материалов и аналогичные характеристики металлов в зоне сварных
швов. Состав и объем необходимой информации должен быть составлен или скорректирован с учетом выбранных для реализации расчетных схем.
3.1.3.5. Данные о начальной и/или текущей дефектности материала труб, включая перечень возможных дефектов, данные о плотности и размещении дефектов в теле трубы.
3.1.4. К основным характеристикам трассы в целом относятся следующие группы факторов:
3.1.4.1. Климатические условия вдоль трассы газопровода - годовые, сезонные и дневные прогнозные оценки перепадов температур воздуха и почвы, влажность, объем осадков (дождевые, снеговые, ледовые). В случае отсутствия достоверной и полной информации должны быть сделаны расчетные оценки показателей на весь прогнозируемый срок эксплуатации.
3.1.4.2. Геоморфологические и гляциокриологические условия вдоль трассы: качественные и количественные характеристики рельефа в зоне прокладки трассы, предварительные оценки возможных подвижек грунта и их воздействий на трассу. Грунтовые условия, включая минеральный состав и физико-механические характеристики грунтов в зависимости от проектных режимов эксплуатации трубопровода и климатических условий вдоль трассы и т.п. Основные характеристики должны быть определены как функции времени и пространственной координаты.
3.1.4.3. Дополнительная информация о территории предполагаемой прокладки трассы трубопровода: полные топографические данные о населенных пунктах, энергетических, транспортных и т.п. магистралях, других технических объектах, которые могут стать объектом поражения при аварии газопровода. Исходная информация должна включать сведения о типе и масштабе возможных последствий при повреждении объектов вдоль трассы трубопровода.
3.2. Нагрузки и воздействия
3.2.1. Трубопровод во время эксплуатации испытывает нагрузки и воздействия, которые, в общем случае, представляют собой пространственно-временные функции. Поэтому, учитывая продолжительность сроков эксплуатации трубопроводов и высокую изменчивость нагрузок и воздействий, исходная информация о нагрузках и воздействиях должна быть подготовлена с учетом фактора времени.
3.2.2. Различают стандартные и нестандартные условия работы трубопровода. В первом случае для расчета параметров проектируемого трубопровода реализуют базовую упрощенную процедуру исследования и расчета напряженно-деформированного состояния трубопровода. Для нестандартных условий работы должна быть применена расширенная процедура анализа нагрузок и воздействий на трубопровод и расчета напряженно-деформированного состояния.
3.2.3. К нестандартным относятся условия, при которых прокладка трассы трубопровода планируется по территориям со следующими характерными особенностями:
3.2.3.1. Заболоченные и подтопленные территории;
3.2.3.2. Территории с подповерхностными пустотами различного происхождения (подрабатываемые территории в зонах шахтного строительства, территории с карстовыми пустотами и т.п.);
3.2.3.3. Зоны вечномерзлых грунтов;
3.2.3.4. Оползневые зоны;
3.2.3.5. Сейсмоопасные зоны;
3.2.4. Перечень особых зон является открытым. По выбору проектировщика он может быть дополнен новыми позициями. Для каждой из позиций 3.2.3.1.- 3.2.3.5. должна быть реализована специализированная методика анализа нагрузок и воздействий на трубопровод.
3.2.5. Нагрузки и воздействия на трубопровод разделим на две группы:
функциональные и природно-климатические.
3.2.5.1. Перечень и уровень функциональных нагрузок обеспечивается и регулируется конструктивной схемой трубопровода и реализованными на практике режимами эксплуатации. К функциональным нагрузкам относится внутреннее давление перекачиваемого продукта, регулируемые температурные воздействия и др. Данные о типах и уровнях функциональных нагрузок должны быть получены из проектной документации.
3.2.5.2. Природно-климатические нагрузки обусловлены взаимодействием трубопровода с окружающей средой. Данные о типах и уровнях природно-климатических нагрузок могут быть получены на основе анализа принятых конструктивных решений, информации о планируемой трассе, включающей основные природно-климатические характеристики регионов и принятых физических, механических и математических моделей рассматриваемых явлений.
Содержание, форма и объем представления данных о природно-климатических нагрузках и воздействиях зависит от принятой к реализации расчетной модели.
3.2.5.3. Реальные совокупные нагрузки и воздействия на трубопровод представляют собой сложную комбинацию двух рассмотренных типов. Оценка реального воздействия на трубопровод должна быть получена с учетом взаимного влияния и сочетаемости нагрузок и воздействий различного происхождения. Выявление возможных комбинаций и сочетаний нагрузок с учетом их развертывания во времени и пространстве - обязательный и неотъемлемый этап анализа нагрузок и воздействий.
3.2.6. При анализе нагрузок и воздействий на трубопровод помимо расчетных нагрузок, регламентированных СНиП, необходимо учитывать дополнительные нагрузки и воздействия, появление которых вызвано реализацией непроектных режимов функционирования конструкции. Такие нагрузки и воздействия будем называть непроектными нагрузками и воздействиями. К числу непроектных нагрузок и воздействий отнесем следующие позиции:
3.2.6.1. Редкие, а потому не учитываемые в регулярных расчетах, сочетания известных нагрузок и воздействий;
3.2.6.2. Аномально высокие уровни нагрузок, учитываемых регулярным расчетом;
3.2.6.3. Действие номинальных нагрузок на частично работоспособную конструкцию с характерными для данного типа конструкций повреждениями.
3.2.7. Анализ непроектных режимов функционирования конструкции необходим для обеспечения уже на этапе проектирования ее устойчивости и живучести по отношению к критическим и катастрофическим отказам.
3.2.8. В настоящее время расчетные нагрузки и воздействия на конструкцию трубопровода регламентируются СНиП. В зависимости от выбранной конструктивной схемы и способа прокладки трубопровода учитывают следующие группы нагрузок и воздействий.
3.2.8.1. Для подземных трубопроводов, проложенных в траншее:
- внутреннее давление перекачиваемого продукта;
- температурные нагрузки, вызванные несовпадением эксплуатационной температуры стенок трубопровода и температуры замыкания конструкции при монтаже;
- нагрузки, вызывающие искривление продольной оси трубопровода;
- весовые нагрузки от грунта засыпки.
3.2.8.2. Для надземных трубопроводов, проложенных на свайном основании:
- внутреннее давление перекачиваемого продукта;
- собственный вес конструкции;
- вес транспортируемого продукта с учетом различных технологических режимов эксплуатации трубопровода;
- дополнительные весовые нагрузки от размещенного на газопроводе оборудования и строительных конструкций;
- нагрузки, вызванные обледенением и налипанием снега;
- температурные нагрузки, вызванные несовпадением эксплуатационной температуры стенок трубопровода и температуры замыкания конструкции при монтаже;
- ветровые нагрузки.
3.2.9. Для нестандартных условий перечни нагрузок в 3.2.8.1. и 3.2.8.2. могут быть дополнены рядом позиций:
3.2.9.1. Для трубопроводов на опорах должно быть исследовано поведение трубопровода при выпучивании, просадке или разрушении одной из промежуточных опор. В результате таких повреждений происходит изменение кривизны продольной оси, а, следовательно, возрастают изгибные напряжения; увеличение длины пролета приводит к понижению собственных частот упругих колебаний и возможности возникновения ветрового резонанса с последующим динамическим или усталостным разрушением; в случае просадки опоры при определенных режимах возможно возникновение ударного взаимодействия трубы с просевшей опорой, что может привести к ускоренному усталостному разрушению трубы в зоне контакта. К аналогичным последствиям может приводить сброс трубопровода с одной или нескольких опор.
3.2.9.2. В случае подземных трубопроводов к нестандартным условиям следует отнести варианты прокладки трубопроводов в зоне пучинистых грунтов и на участках, подверженных морозобойному растрескиванию. В этих условиях дополнительные нагрузки от грунта могут привести к разрыву или чрезмерному деформированию трубопровода. К непроектным режимам следует отнести ситуации, при которых происходит обводнение траншеи и размыв засыпки с частичной или полной потерей балластирующей способности. В этом случае возможен выброс трубопровода из траншеи на ослабленном участке с последующим разрушением или возникновением повреждений в зонах с местной потерей устойчивости.
3.3. Классификация отказов и предельных состояний
3.3.1. Классификацию состояний трубопровода построим на основе рекомендаций, представленных в терминологическом стандарте / 3/. В соответствии с ними будем различать понятия исправного и работоспособного состояния объекта:
3.3.1.1. Исправным называется состояние, при котором объект полностью соответствует всем требованиям нормативно-технической и (или) конструкторской (проектной) документации.
3.3.1.2. Неисправным называется состояние, при котором объект не соответствует хотя бы одному из требований нормативно-технической и (или) конструкторской (проектной) документации.
3.3.1.3. Работоспособным называется состояние, при котором значения всех параметров, характеризующих способность объекта выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской (проектной) документации.
3.3.1.4. Неработоспособное состояние - состояние объекта, при котором значение хотя бы одного из параметров, характеризующих способность объекта выполнять заданные функции, не соответствует требованиям нормативно-технической и (или) конструкторской (проектной) документации.
3.3.2. Для сложных объектов, в частности для трубопроводов, допускается более глубокая классификация неработоспособных состояний с выделением частично работоспособных состояний, при которых объект способен частично выполнять требуемые функции.
3.3.3. Из приведенных в п. 3.3.1 и п. 3.3.2 определений следует, что понятие исправного состояния шире понятия работоспособного состояния и включает его в качестве подмножества. В отличие от исправного объекта, который всегда находится в работоспособном состоянии, неисправный объект может находиться как в работоспособном, так и в неработоспособном состоянии.
3.3.4. Повреждением называется событие, состоящее в нарушении исправного состояния при сохранении работоспособного состояния объекта.
3.3.5. Отказом называется событие, состоящее в нарушении работоспособного состояния объекта.
3.3.6. Признак или совокупность признаков нарушения исправного состояния при сохранении работоспособного состояния объекта называется критерием повреждения.
3.3.7. Признак или совокупность признаков нарушения работоспособного состояния объекта называется критерием отказа.
3.3.8. Основное требование к трубопроводам как к транспортным системам повышенной ответственности, с точки зрения обеспечения безопасности, заключается в сохранении герметичности и конструкционной целостности в течение всего срока службы. Поэтому любое событие, связанное с нарушением герметичности конструкции трубопровода, должно быть классифицировано как отказ.
3.3.9. Классификация отказов по степени критичности должна быть построена на анализе последствий предполагаемого отказа. Отказы ЛЧМГ, последствия которых могут создать угрозу жизни и здоровью людей, либо привести к опасным для человека изменениям в окружающей среде, будем классифицировать как критические и (или) катастрофические отказы. Содержание критериев для деления отказов по степени критичности зависит от целого ряда факторов. В их число могут входить параметры, характеризующие размещение различных объектов вдоль трассы, плотность населения, попадающего в предполагаемую зону поражения, конкретные особенности конструктивной схемы трубопровода, учитывающие возможности по диагностированию аварийной ситуации и локализации ее развития, параметры, характеризующие территории по которым проложена трасса трубопровода, с точки зрения вида и уровня возможного ущерба для окружающей среды.
В зависимости от типа территорий, по которым проложен трубопровод, отказ, вызванный локальной негерметичностью конструкции типа свища, в условиях малообитаемых пустынных территорий может быть классифицирован как некритический. Напротив, аналогичный отказ на трубопроводе, проходящем через густонаселенные территории и при условиях, допускающих скопления газа до взрывоопасных концентраций, должен быть классифицирован как критический или даже катастрофический отказ.
3.3.10. Состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособности невозможно или нецелесообразно называется предельным для данного объекта. Для сложных объектов может быть введено несколько типов предельных состояний.
3.3.11. Аналогично п. 3.3.6 п. 3.3.7 для каждого типа предельного состояния должен быть установлен признак или совокупность признаков, называемых критерием предельного состояния.
3.3.12. Для потенциально опасных сооружений и конструкций, к которым принадлежат газо- и нефтепроводы, к категории предельных могут быть отнесены состояния, реализация которых не приводит к необходимости безоговорочного прекращения функционирования по назначению и снятию объекта с эксплуатации. Для таких состояний характерно сохранение работоспособности конструкции, а, следовательно, отсутствие признаков отказа в рамках регламентируемой / 3/ терминологии. Выделение данной группы состояний связано с тем, что дальнейшая эксплуатация объекта сопряжена с существенным повышением риска возникновения критических и (или) катастрофических отказов. К таким состояниям могут быть отнесены предельные состояния, сформулированные в традиционном для строительной механики и механики разрушения смысле. На практике в большинстве нормативных документов, регламентирующих систему прочностных, деформационных и связанных с ними расчетов, понятие предельного состояния используется в основном в смысле близком тому, что представлен в данном разделе.
3.3.13. Введем в рассмотрение следующие группы критериев предельных состояний. Перечень составлен на основе анализа условий работы трубопроводов и выделении базовых обобщающих признаков предельных состояний с учетом п. 3.3.12:
3.3.13.1. - избыточные пластические деформации;
3.3.13.2. - местная потеря устойчивости;
3.3.13.3. - общая потеря устойчивости;
3.3.13.4. - усталостное разрушение (малоцикловое и многоцикловое);
3.3.13.5. - хрупкое разрушение;
3.3.13.6. - вязкое разрушение;
3.3.13.7. - коррозионное растрескивание.
События, связанные с реализацией избыточных пластических деформаций (или превышением заданного уровня напряжений), местной и общей потерей устойчивости следует трактовать как повреждения. К этой же группе должны быть отнесены события, связанные с реализацией усталостных явлений, развитием хрупких и вязких разрушений и коррозионного растрескивания, если они не привели к нарушению герметичности конструкции, а рассматриваются в процессе развития. В противном случае эти события должны быть признаны отказами.
3.3.14. Классификация предельных состояний должна быть проведена отдельно по типам конструктивных элементов:
- основной металл,
- продольные (заводские) сварные стыковые соединения,
- отводы.
- тройниковые соединения,
- переходники (и др. элементы по выбору проектировщика).
3.3.15. Форма представления критериев предельных состояний определяется типом связанной с данным критерием прочностной, динамической или статической задачи, выбранной для реализации механико-математической модели конструкции, действующих на трубопровод нагрузок и воздействий.
Ниже рассмотрены формализации некоторых основных критериев предельных состояний (символы j i , расположенные слева от записи, представляют собой формальное имя критерия, в дальнейшем используемое для ссылок на данный критерий):
3.3.15.1. Критерий допускаемых напряжений:
y 1 : ½ s э i ½ £ [ s ],
где s э i - эффективное напряжение в стенке трубы, вычисленное по заданному критерию прочности; [ s ] - максимальное допускаемое напряжение, заданное в форме, согласованной с выбранным критерием прочности;
3.3.15.2. Критерий больших пластических деформаций:
y 2 : ½ e э i ½ £ [ e у ],
где e э i - эффективная деформация в стенке трубы;
[ e у ] - допускаемое предельное значение деформации;
3.3.15.3. Усталостный критерий для бездефектного материала:
y 3 : N £ N * ,
где N - число циклов или блоков квазициклического нагруженная,
N * - предельное число циклов по испытаниям материала на усталость;
3.3.15.4. Усталостный критерий для дефектного материала:
y 4 :N( l k ) £ N * k ,
где N ( l k ) - число циклов или блоков квазициклического нагружения с учетом дефекта структуры k-го типа, N * k - предельное число циклов по испытаниям материала с дефектом k-го типа на усталость; ( l k ) - вектор характеристических управляющих параметров дефекта k-го типа;
3.3.15.5. Критерий трещиностойкости для трещиноподобных дефектов и трещин (герметичность):
y 5 :Nc(ck) £ N * ck
где Nc ( ck ) - число циклов или блоков квазициклического нагружения до сквозного прорастания дефекта k-го типа, N * ck - допустимое число циклов; cr -вектор характеристических управляющих параметров трещины или трещиноподобного дефекта k-го типа. Допускается альтернативная формулировка критерия y 5 вида:
y 5 : ck £ 0,8 d ,
где ck - глубина трещины, d - толщина стенки трубы;
3.3.15.6. Критерий трещиностойкости для трещиноподобных дефектов и трещин (устойчивость):
y 5 :maxK1(ck) £ K1ck ,
где maxK 1 ( ck ) - максимальный коэффициент интенсивности напряжений на фронте трещины нормального отрыва, K 1 ck - критический КИН для трещин нормального отрыва в данном материале. Можно сформулировать более общий критерий для трещины других или совместных мод.
3.3.16. Перечень критериев пункта 3.3.13. является открытым для расширения при учете новых типов предельных состояний.
3.3.17. Практическая реализация критериев предельных состояний основана на разработке и применении соответствующих расчетных моделей. Общие требования к выбору и построению расчетных схем и оценки параметров напряженно-деформированного состояния будут рассмотрены ниже.
3.3.18. Если критический отказ ЛЧМГ является зависимым отказом, то необходимо в расчетной методике рассмотреть дерево (деревья) отказов с учетом критериев предельных состояний промежуточных отказов.
3.4. Требования к построению расчетных схем для оценки напряженно-деформированного состояния участка газопровода
Требования к расчетным схемам, механико-математическим моделям и методам решения поставленной задачи определяются задаваемыми проектом геометрией трассы, способом прокладки, режимами эксплуатации, региональными условиями взаимодействия с окружающей средой, а также внесенными в проектное задание необходимыми для оценивания критериями отказов и предельных состояний. Расчетные схемы должны соответствовать классификации участков трассы по принципу однородности условий возникновения отказов (предельных состояний) одного типа. Конкретный выбор расчетной схемы подчиняется нормам СНиП для магистральных трубопроводов и соответствующей нормативной и методологической литературе.
3.5. Формирование расчетных участков
3.5.1. Линейная часть магистрального газопровода /ЛЧМГ/ представляет собой протяженную пространственную конструкцию, работающую в течение заданного срока t . Неоднородность нагрузок и воздействий на различных участках газопровода является причиной различий в уровне надежности и долговечности элементов газопровода.
Разобьем газопровод на расчетные участки. Цель разбиения состоит в выделении участков с однородными условиями эксплуатации. Однородность участка должна быть обеспечена в течение всего временного интервала, на котором прогнозируются соответствующие показатели надежности и долговечности.
3.5.2. Трасса ЛЧМГ разбивается на участки с однородными условиями по способу прокладки и конструктивным особенностям газопровода, грунтово-геологическим условиям, нагрузкам и воздействиям. Обязательным условием обеспечения однородности в пределах выделенного участка является наличие единой конструктивной схемы газопровода, постоянство геометрических характеристик и физико-механических свойств труб.
3.5.3. При первичном разбиении ЛЧМГ на участки по вышеперечисленным признакам рекомендуется руководствоваться делением на категории, принятом в СНиП.
3.5.4. Дальнейшее разбиение производится после анализа нагрузок и воздействий, свойств конструкции в целом и отдельных ее частей в пределах выделенного участка.
3.5.5. Будем различать два уровня разбиений конструкции на расчетные участки. Первый - соответствует разбиению конструкции на элементы в соответствии с выбранными при оценке напряженно-деформированного состояния расчетными схемами.
3.5.6. Цель разбиений второго уровня состоит в выделении участков с однородными характеристиками по выбранной группе параметров. Перечень параметров, учитываемых при разбиении, зависит от характеристик конструкции, вида предполагаемых расчетов, типов возможных отказов и предельных состояний, реализуемых на выделенном расчетном участке. При этом вначале формируют перечень типов расчетных участков, объединенных заданными общими признаками.
3.5.7. Учитывая общий характер нагрузок, действующих на надземный газопровод, выделим следующие возможные группы расчетных участков. В качестве примера взят надземный газопровод.
3.5.7.1. Примем в качестве первой расчетной области элемент оболочки мерой L 0 с наибольшим уровнем контактных напряжений в зоне прилегания к опоре. В первом приближении аппроксимируем область L0 цилиндрической панелью радиуса R , равным радиусу срединной поверхности оболочки. Размеры области в продольном 21х и поперечном 21у направлениях определяются масштабом неоднородности напряженного состояния в оболочке газопровода в зоне опирания на опору.
3.5.7.2. Учитывая распределение и характерный масштаб неоднородности изгибных напряжений по длине пролета надземного трубопровода, в качестве второго типа расчетного участка примем участок газопровода заключенный между опорами. При этом полагаем, что во всех сечениях расчетного участка действуют напряжения максимальной в пределах участка интенсивности. Для учета неоднородности напряжений в продольном направлении, участок трубопровода между опорами необходимо разбить на более короткие элементы, с меньшим уровнем напряжений.
3.5.7.3. В качестве расчетного участка третьего типа примем элемент оболочки, содержащий сварные швы. Необходимость выделения сварных швов обусловлена различием физико-механических свойств и уровня дефектности основного металла и материала в области шва. В качестве меры расчетной области примем длину сварного шва.
3.5.8. При оценке надежности под длиной расчетного участка понимается общая протяженность перечисленных эталонных расчетных участков отдельно по каждому из трех типов. При этом уровни напряжений и параметры начальной дефектности принимаем равными соответствующим максимальным значениям, определенным на всей совокупности расчетных участков.
3.5.9. При невозможности обеспечить однородность по всем требуемым параметрам ЛЧМГ разбивают на блоки, в которых обеспечивается однородность по ограниченному числу заранее выбранных параметров. По отношению к остальным параметрам поступают следующим образом. Производят оценку напряженно-деформированного состояния конструкции в пределах выделенного участка с учетом действительных нагрузок, выбирают наиболее неблагоприятное сочетание нагрузок и принимают в качестве расчетного. Все точки в пределах расчетного участка считают равнонагруженными и приписывают им уровень напряжений, максимальный для данного участка.
3.6. Формирование пространства состояний расчетного участка
3.6.1. При формировании пространства состояний трубопровод рассматривается как целостная система, объединяющая непосредственно ЛЧМГ и совокупность нагрузок и воздействий, включая непредусмотренные нормативными документами.
3.6.2. Сформируем набор параметров s 1 (1=1,..., r ) которые с достаточной полнотой характеризуют свойства системы в пределах выделенного участка. Среди параметров s 1 могут быть как детерминистические и случайные величины, так и детерминистические и случайные функции, зависящие от времени.
3.6.3. Для случайных величин, входящих в число параметров s 1 должны быть заданы соответствующие плотности распределения вероятности.
3.6.4. Для стационарных случайных функций, входящих в число параметров s 1 , должны быть заданы корреляционные функции.
3.6.5. Форма представления исходной информации о нестационарных функциях, входящих в число параметров s 1 , зависит от вида функции и должна быть в каждом конкретном случае определена дополнительно.
3.6.6. Идентифицирующим признаком отдельного состояния или класса состояния будем считать совокупность конкретных значений параметров s 1 .
3.6.7. В настоящем документе ограничимся случаем конечного числа возможных состояний. Переход к конечному числу возможных состояний осуществим путем замены параметров s 1 , имеющих непрерывное распределение дискретной аппроксимацией. Пространство состояний, искусственно ограниченное конечным числом элементов, должно обладать свойством полноты.
3.6.8. Среди параметров s 1 могут быть зависимые параметры. В этом случае разобьем все параметры на группы по признаку взаимного влияния. К элементам первой группы отнесем независимые параметры. Во вторую группу поместим параметры, зависящие от одного или нескольких параметров из первой группы. В третью - параметры, зависящие от элементов первой и второй, или только второй группы. Перегруппировка параметров заканчивается после исчерпания списка параметров. Внутри каждой группы считаем параметры независимыми. Наличием обратной связи между параметрами пренебрегаем.
3.6.9. В пределах группы множество возможных значений произвольного зависимого параметра s 1 представим в виде объединения M 1 независимых подгрупп, каждая из которых содержит K 1 элементов. Параметр M 1 равен числу возможных комбинаций параметров, влияющих на величину параметра s 1 .
3.6.10. В результате, любое из возможных состояний трубопровода представимо в виде последовательного соединения элементов, принадлежащих различным группам, по одному из каждого вертикального слоя, соответствующего множеству возможных значений параметра s 1 .
3.6.11. В дальнейшем общее число
классов Ф j возможных состояний
обозначается ![]() .
.
3.7. Перечень и структура нормируемых показателей надежности
3.7.1. Выбор показателей надежности (по отношению к отдельным группам отказов на одном участке ЛЧМГ):
3.7.1.1.- некритические отказы:
P ( t ) - вероятность безотказной работы ЛЧМГ за эксплуатационный период [0, t ].
Тс - средний срок службы.
3.7.1.2. - критические отказы:
P ( t ) - вероятность безотказной работы ЛЧМГ за эксплуатационный период [0, t ] с учетом старения материала;
T 1 c - средний срок службы до первого критического отказа.
3.7.1.3. - катастрофические отказы:
P ( t g ) - вероятность безотказной работы ЛЧМГ за период [0, t g ];
t g - g -процентный ресурс до первого отказа.
3.7.2. Показатели безопасности должны включать вероятностные характеристики события, состоящего в нанесении максимального ущерба обслуживающему персоналу, населению и/или окружающей среде в районе трассы в случае аварии трубопровода. Вероятность последней определяется по отношению ко всем типам возможных критических отказов и носит название технического риска.
3.7.2.1. Вероятность Ps ( t ) безопасной работы трубопровода за время t (трактуется как вероятность безотказной работы по отношению к катастрофическим отказам);
3.7.2.2. Конструкционный технический риск H ( t )=1- Ps ( t ) - альтернативный показатель по отношению к вероятности безопасной работы (используют либо первый, либо второй показатели);
3.7.2.3. Вероятность P ( t , Q , t * , r ) ущерба величины Q в момент t при условии аварии трубопровода в момент t, на удалении r от объекта.
3.8. Методы расчета показателей надежности
3.8.1. Рекомендуемая последовательность прогнозирования показателей надежности:
3.8.1.1. Выделение участков с однородными условиями эксплуатации;
3.8.1.2. Перечень возможных типов отказов и предельных состояний, их вызывающих ( согласно п. 5);
3.8.1.3. Формализация критериев наступления предельного состояния;
3.8.1.4. Выбор показателей надежности по отношению к данному типу предельного состояния на данном участке с учетом критичности отказа и характера последствий;
3.8.1.5. Выбор метода расчетного прогнозирования по отношению данного показателя надежности;
3.8.1.6. Оценка исходной информации, подготовка информационной базы расчета показателей надежности (статистические данные по объектам-аналогам);
3.8.1.7. Получение расчетной оценки показателя надежности;
3.8.1.8. Получение расчетной оценки показателя надежности всего участка по отношению к группе отказов всех типов предельных состояний и ко всем группам отказов в целом;
3.8.1.9. Интегральная оценка показателей надежности всей трассы трубопровода;
3.8.1.10. По отношению к критическим и катастрофическим отказам (авариям) оценка показателей безопасности: интегрального технического риска, индивидуального профессионального и общего регионального риска, суммарного экономического, социального и экологического ущерба;
3.8.1.11. Выбор показателей ремонтопригодности;
3.8.1.12. Оценка показателей ремонтопригодности с учетом оцененных показателей долговечности по отношению к различным типам отказов и к каждому участку ЛЧМГ;
3.8.1.13. Разработка программы обеспечения надежности (ПОН) на весь период эксплуатации;
3.8.1.14. Разработка программы обеспечения безопасности (ПОБ) на весь период эксплуатации;
3.8.1.15. Расчет материально-технического обеспечения трассы на весь период эксплуатации.
3.8.2. Для постепенных критических отказов, вызванных прорастанием усталостных и коррозионных трещин, локальными разгерметизациями, образованием локальных пластических зон и вторичных дефектов, взаимодействием трубопровода с промерзающим пучинистым грунтом применяются формулы вычисления показателей надежности на основе теории выбросов случайного процесса за пределы допускаемой области в предположении пуассоновского потока событий.
3.8.2.1. Формулы для расчета показателей надежности имеют вид:
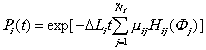 ,
,
где D Li - длина i-го участка ЛЧМГ; t
- временной параметр продолжительности эксплуатации; m ij - интенсивность возникновения предельных состояний класса
Ф j на i-ом участке ЛЧМГ; Н ij - вероятность отказа, соответствующего нарушению
предельного состояния класса Ф j ; ![]() - число классов Ф j . Парциальный риск Н ij соответствует вероятности того, что среди множества
возможных состояний i-го участка на практике будет реализовано состояние,
принадлежащее классу Ф j .
- число классов Ф j . Парциальный риск Н ij соответствует вероятности того, что среди множества
возможных состояний i-го участка на практике будет реализовано состояние,
принадлежащее классу Ф j .
3.8.2.2. Для трубопровода длиной L = ![]() , риск вычисляем по формуле:
, риск вычисляем по формуле:
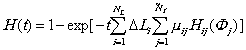 .
.
3.8.2.3. Оценка гамма-процентного ресурса t g и средней наработки до первого отказа T 1 производим по следующим формулам:
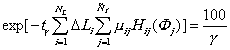
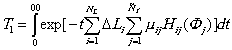
3.8.2.4. Вычисление математических
ожиданий m ij связано с вероятностью числа
отказов j-го класса Ф j на i-ом
участке Qij ( t ) и начальным математическим ожиданием
исходных событий - источников возникновения критических отказов - ![]() соотношением:
соотношением:
![]() .
.
3.8.2.5. Вероятность числа отказов Qij вычисляется индивидуально для каждого отдельного класса Ф j и на i-ом участке и определяется функцией распределения вероятности по отношению к формализованному критерию предельного состояния типа Ф j . Для определения вероятностей Qij требуется знание функции распределения или плотности распределения вероятности. Если таковых формализованных соотношений нет, то применимы приближенные методы статистического моделирования (Монте-Карло), для реализации которых достаточно статистической информации о потоке исходных событий. При наличии плотности распределения исходных событий и сравнительно сложных (например, полуэмпирических или эмпирических) зависимостях предельных поверхностей, ограничивающих область допустимых состояний, могут быть рекомендованы приближенные вычислительные процедуры методов FORM - SORM .
3.8.2.6. Вычисление парциальных вероятностей Н ij (Ф j ) основано на применении метода условных функций надежности, согласно которому при недостатке исходной полной статистической информации о реализации событий, описывающих изменение управляющего параметра как непрерывной функции, производится замена непрерывного интервала значений параметра совокупностью кусочно-непрерывных интервалов, для каждого из которых значение вероятности реализации события, состоящего в том, что параметр принимает значения из этого интервала считается известным и постоянным. Вариант разбиения при этом должен удовлетворять требованию полноты пространства состояний
![]()
Последнее условие эквивалентно требованию равенства единице суммы парциальных вероятностей реализации возможных событий.
Ввиду сложности и новизны проблемы данная методика имеет общеметодологический характер.
Для наиболее трудных случаев, прокладка в промерзающих пучинистых грунтах, для надземных газопроводов при действии ветровой нагрузки и просадке опор и т.д., дан подробный материал в особых разделах.
ПЕРЕЧЕНЬ ПРОГРАММНЫХ ПРОДУКТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ РАСЧЕТНОГО ПРОГНОЗИРОВАНИЯ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ И ДОЛГОВЕЧНОСТИ ЛИНЕЙНЫХ ЧАСТЕЙ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ
ВНИИгаз располагает следующими программными продуктами, позволяющими проводить расчеты, включенные в настоящую методику.
1. Группа программ, составляющих программный комплекс P 1 PEGR , предназначена для оценки напряженно-деформированного состояния участка трубопровода с учетом взаимодействия с промерзающим пучинистым грунтом. В программном комплексе реализовано несколько расчетных моделей. Первая модель позволяет проводить расчеты напряженно-деформированного состояния трубопровода, взаимодействующего с единичным бугром пучинистого грунта. Влияние грунта учтено по схеме жесткого несминаемого тела и жесткого тела с ограниченным сопротивлением смятию. По результатам расчета могут быть построены области допустимых размеров бугров пучения.
2. Программный комплекс PFCG предназначен для решения следующих задач:
- моделирование начальной поверхностной полуэллиптической трещины;
- расчет роста усталостной трещины до момента прорастания дефекта сквозь стенку трубопровода или до конца заданной длины реализации напряжений;
- построение границ допустимых начальных размеров трещин при заданной продолжительности эксплуатации;
- статистическая обработка случайной выборки времен прорастания дефектов до сквозных с целью получения параметров функции распределения времен отказов трубопроводов.
Конечными результатами работы комплекса PFCG являются границы областей допустимых значений начальных размеров трещин и значения вероятности безотказной работы участка ЛЧМГ за заданную продолжительность эксплуатации.
3. Программы класса RISK позволяют проводить вероятностный анализ на основе вычислительного эксперимента. Сюда входят программы моделирования исходных выборок для обширного диапазона заданных типов распределений (равномерное, нормальное, логнормальное, вейбулловское и др.); программы моделирования реализации случайных процессов (белый шум, стационарные процессы с заданными спектральными свойствами или корреляционной функцией, нестационарные процессы с заданным типом огибающей); программы цензурирования исходных выборок по заданным критериям (выделение ведущих гармоник, выделение шума, отсечение или выделение "хвостов" распределений и т.д.); программы обработки исходных выборок и реализации для получения оценок типов распределений и/или спектральных свойств; программы вычисления показателей надежности.
4. Конечно-элементный программный комплекс SEISTRAN ( Seismic Structural Response Analusis ) предназначен для комплексного расчета на сейсмостойкость инженерных конструкций различного назначения (строительные конструкции, разветвленные трубопроводные системы и др.). Текущая версия пакета SEISTRAN (версия 2.1.) позволяет решать следующие классы задач:
- определение реакций строительных конструкций на действие произвольной статической нагрузки с учетом собственного веса;
- спектральный анализ исследуемых конструкций;
- динамический анализ реакций строительных конструкций на изменяющееся во времени силовое возбуждение (реализованы методы прямого интегрирования и разложения по собственным формам колебаний);
- динамический анализ реакций строительных конструкций на сейсмическую нагрузку (реализовано многокомпонентное кинематическое возбуждение в виде инструментальных или математических сгенерированных акселерограмм, позволяющее учесть не только спектральные, но и волновые характеристики сейсмического воздействия, что особенно существенно для протяженных конструкций).
Для программного комплекса характерно высокое быстродействие;
компактность, позволяющая использовать не только мощные машины, но и малые персональные ЭВМ, начиная с PC AT 286; наличие графического пре- и постпроцессоров для визуализации входной информации и результатов расчета; дружественный интерфейс (контроль входной информации с локализацией места ошибки, система контекстно-зависимой подсказки, встроенный справочник и др.).
5. Комплекс программ группы FATIGUE по оценке долговечности высоконагруженных конструкций при циклическом нагружении. Реализованы модели классической усталости. Предусмотрено регулярное, блочное и нерегулярное (в том числе нестационарное) воздействие. При нерегулярном нагружении расчет накопления повреждений проводится с использованием методов падающего дождя и полных циклов.
6. Комплекс WIND включает в себя модули, решающие следующие функциональные задачи: моделирование ветрового потока в течение заданной продолжительности эксплуатации, вычисление нагрузок, расчет колебаний участка ЛЧМГ и оценку напряженно-деформированного состояния трубопровода с учетом контактного взаимодействия с просевшей опорой. Выходными данными в комплексе WIND являются собственные частоты и формы колебаний трубопровода, реализация перемещений, значения контактных нагрузок на трубопровод и напряжений в оболочке в зоне контакта при ударном взаимодействии с просевшей опорой.
7. Программный комплекс NLLSGM по оценке характеристик циклической трещиностойкости конструкционных материалов. Реализовано определение констант, входящих в наиболее распространенные модели роста усталостных трещин. На вход в виде базы данных подается экспериментальная диаграмма усталостного разрушения (экспериментальные данные получены на стандартных образцах по прилагаемой методике). Решение строится на основе высокоэффективных алгоритмов и представляется в графической форме. Полученные характеристики предназначены для расчета долговечности (живучести) конструкций с трещинами при циклическом (возможно нерегулярном) нагружении.
8. Программный комплекс NLFRAC предназначен для прогнозирования долговечности высоконагруженных подземных конструкций с трещинами в условиях эксплуатации, требующих учета вязких и пластических свойств материала и накопления рассеянных повреждений.
Блочная структура комплекса позволяет варьировать модели деформирования материала и накопления повреждений.
Поскольку вычисления проводятся методом конечных элементов, возможно моделирование роста трещин при широких предположениях о форме тела, размещении и конфигурации трещин, заданных нагрузках и перемещениях.
В процессе решения задачи возможен контроль полей напряжений, деформаций и микроповреждений в окрестности вершины трещины.
Список использованных источников
1. Байхельт Ф., Франкен П. Надежность и техническое обслуживание. Математический подход. Пер. с нем. М.: Радио и связь. 1988. - 392 с.
2. Болотин В. В. Ресурс машин и конструкций. М.: Машиностроение. 1990.- 448 с. (2-ое изд., перераб. и доп.)
3. ГОСТ 27.002-89. Надежность в технике. Основные понятия. Термины и определения. М. : МНТК "Надежность машин". 1988. - 58 с.
4. Иванцов О.М. Надежность строительных конструкций магистральных трубопроводов. М.: Недра. 1985.- 301 с.
5. Надежность и эффективность в технике. Справочник в 10 т. /Ред. совет: В С. Авдуевский (пред.) и др. М.: Машиностроение. Т. 1. Методология. Организация. Терминология/ Под ред. А.И. Рембезы. 1987. - 224 с. ; Т. 2. Математические методы в теории надежности и эффективности /Под ред. Б.В. Гнеденко. М.: Машиностроение. 1987. - 280 с.
6. Надежность технических систем. Справочник /Ю.К. Беляев, В. А. Богатырев, В. В. Болотин и др./ Под ред. И. А. Ушакова. М. : Радио и связь. 1985. - 608 с.
7. Программно-методический комплекс для расчета линейных частей магистральных трубопроводов, прокладываемых в сложных природно-климатических условиях / ИМАШ АН СССР. 1989. -.106 с.
8. Харионовский В.В. Повышение прочности газопроводов в сложных условиях. Л.: Недра. 1990. -180 с.
9. Abes A.J., Salinas J.J., Rogers J.T. Risk assessment methodology for pipeline systems // Structural Safety. 1985. Vol . 2. №3. P . 225-237.
10. Алгоритмы и структура программного обеспечения расчетов на прочность элементов конструкций при циклическом нагружении на ПЭВМ / Методические указания МНТК "Надежность машин", М.: ИМАШ, МЦНТИ, 1991.-71с.
11. СНиП 2.05.06-85. Магистральные трубопроводы. Госстрой СССР, М.: ЦИТП Госстроя СССР, 1985.- 52 с .
12. Rules for Submarine Pipeline Systems. Norvik: Norske Veritas, 1981.- 88 p.
13. Pipelines and Transmission / European Standard Groningen: CEN, 1993.- 138р.
КОММЕНТАРИИ К "МЕТОДИЧЕСКИМ РЕКОМЕНДАЦИЯМ ПО РАСЧЕТАМ КОНСТРУКТИВНОЙ НАДЕЖНОСТИ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ"
Требования, предъявляемые к таким ответственным энергетическим сооружениям, как магистральные нефтегазопроводы обусловливают разработку новых вопросов о их надежности, исходя из современных достижений. В первую очередь сюда необходимо отнести вопрос о прогнозировании показателей надежности, разработке алгоритмов их количественного описания для применения в проектировании. Поскольку эта работа выполняется, по-видимому, впервые, целесообразно для практических целей представить развернутые Комментарии раздела "Методические рекомендации по расчетам конструктивной надежности магистральных газопроводов".
Структура и содержание Методических рекомендаций не предусматривают жесткой регламентации применяемых расчетно-экспериментальных методов и программных средств. В настоящей редакции Методические рекомендации содержат общие сведения об исследованиях и получении значений показателей конструктивной надежности линейных частей магистральных газопроводов. В рамках принятой методологии сам разработчик должен выбрать оптимальный с его точки зрения набор расчетно-экспериментальных моделей и методов, а также перечень необходимых программных средств для их практической реализации. В целом такой подход соответствует современным тенденциям в создании нормативных материалов нового поколения в различных отраслях техники и строительства. Однако он накладывает дополнительные требования к уровню квалификации персонала и организации рабочего процесса. Переход к новым более сложным исследованиям не допускает упрощенного механического подхода с детальной пооперационной регламентацией процесса исследований.
Рекомендуемые методы исследования в значительной степени ориентированы на широкое применение ЭВМ и использование как общедоступных универсальных пакетов программ, так и узкоспециализированных оригинальных программных разработок. Краткие рекомендации по составлению и применению предметно-ориентированных расчетных методик с перечнем литературных источников по соответствующим проблемам приведены в "Комментариях...".
"Комментарии..." состоят из шести разделов, соответствующих основным пунктам "Методических рекомендаций…". В заголовок каждого комментария вынесено название пункта "Методических рекомендаций... ", к которому относится данный комментарий. Некоторые этапы исследования надежности трубопроводов, не требующие более глубокой детализации, оставлены без комментария.
Основное внимание уделено анализу нагрузок и воздействий на трубопровод, выбору и обоснованию расчетных схем и моделей, формализации критериев отказов и предельных состояний. При наличии альтернативных подходов к построению расчетных моделей (этапы схематизации нагрузок и воздействий, расчета напряженно-деформированного состояния, оценки показателей надежности и др.) в "Комментариях... " приведена дополнительная библиография по существу обсуждаемых вопросов.
1. КОММЕНТАРИЙ К П. 3.2 . НАГРУЗКИ И ВОЗДЕЙСТВИЯ
К настоящему времени создан нормативный базис, регламентирующий процедуру проведения прочностных расчетов и проектирования трубопроводных конструкций. Ряд специальных вопросов находится в стадии разработки. К ним относятся в основном вопросы, связанные с уточнением действительных нагрузок и воздействий, построением уточненных моделей взаимодействия трубопровода с окружающей средой в сложных природно-климатических условиях, включая взаимодействие с грунтом.
1.1. Нормативные расчеты для стандартных условий
Нормативные методы расчета трубопроводов обсуждены в / 1, 24, 26/. Перечень нагрузок и воздействий, учитываемых при расчете, формируют в зависимости от типа трубопровода, конкретной конструктивной схемы, условий эксплуатации. Нормативные документы устанавливают общие правила прочностного расчета, в рамках которого выбирают оптимальную расчетную схему / 1, 4- 8, 41, 42/. Толщину стенки трубопровода определяют по безмоментной теории круговых цилиндрических оболочек. Продольные напряжения в трубопроводе определяют по стержневой модели в соответствии с общими правилами строительной механики / 9/. Толщина стенки трубы с учетом времени эксплуатации определяется в / 30ы/.
1.1.1. Подземные трубопроводы
Методы расчета подземных трубопроводов общего назначения изложены в / 1, 8, 11/.
Расчет взаимодействия трубопроводов с грунтом проводят на основе традиционных моделей, применяемых в механике грунтов. Силовое воздействие со стороны грунта на трубопровод учитывают либо путем прямого задания нагрузок, либо введением в расчеты различных моделей грунтовых оснований / 1, 4, 7, 9, 11, 16, 26, 33, 34, 38, 39 и др./.
Наиболее широкое распространение получили модели винклеровского типа с линейной или нелинейной связью между перемещениями трубопровода и величиной реакции грунта. Для грунтов, работающих только на сжатие, применяют модели с односторонними связями / 8, 26/. Результаты экспериментального оценивания коэффициентов отпора для грунтов различного состава приведены в/ 1, 4, 10, 16, и др./.
При прокладке трубопровода в траншее или в насыпи важно оценить предельную несущую способность грунта. Методы расчета по схемам предельного равновесия для грунта и необходимые численные данные в работах / 1, 4, 11, 42/. В пористых, податливых грунтах расчет по этому методу может приводить к заметным погрешностям за счет значительной деформативности грунта без достижения предельного состояния. Для таких грунтов при оценке устойчивости следует применять модели винклеровского типа.
В работах / 1, 33, 34/ приведены экспериментальные зависимости реакции грунтов на перемещения трубопроводов при различных диаметрах трубы. Использование в расчетах полномасштабной диаграммы, рассмотренного вида, позволяет прогнозировать работу трубопровода на различных стадиях эксплуатации, с учетом изменения несущей способности грунта и иных факторов. Примеры практического применения методики приведены в / 1, 19, 33/.
Нормативными документами предусмотрено проведение расчетов устойчивости трубопровода с учетом удерживающей способности грунта / 24/. В работе / 1/ получено решение задачи о продольной устойчивости трубопровода с начальными искривлениями с учетом нелинейной работы грунта и с использованием диаграмм "перемещение трубопровода - реакция грунта". Близкая по постановке задача рассмотрена в / 19, 25/. Вариационным методом проведено исследование устойчивости подземного трубопровода, проложенного на билинейном основании и имеющего начальные неправильности формы, определена длина арочного выброса как функция напряженного состояния конструкции и свойств окружающего грунта.
1.1.2. Надземные трубопроводы
Методы расчета надземных трубопроводов рассмотрены в / 1, 5, 15, 18, 22, 26/. Помимо нагрузок от внутреннего давления и температурного перепада при расчете надземных трубопроводов учитывают суммарные весовые нагрузки, включая нагрузки от налипания снега, обледенения, дополнительные весовые нагрузки, возникающие при различных технологических режимах эксплуатации. В качестве основной расчетной схемы надземного трубопровода применяют модель многопролетного стержня кольцевого поперечного очертания. Продольные напряжения в трубопроводе определяют с учетом работы компенсаторов / 1, 15, 26, 29/.
Особым видом нагружения надземных трубопроводов являются аэродинамические нагрузки, оказывающие статическое и динамическое воздействие / 18, 26/. Методы оценки величины статической и динамической составляющих аэродинамических нагрузок представлены в / 1, 3, 18, 26/.
Вообще говоря, скорость ветрового потока представляет собой случайную, нестационарную и неоднородную по координате функцию времени / 3/. Нормативными расчетами предусмотрено сведение ветровой нагрузки к детерминистическому по форме воздействию. Ветровую нагрузку рассматривают как сумму средней и пульсационной составляющих. Величину пульсационной составляющей определяют с учетом вероятностных характеристик ветрового воздействия / 31/.
Определение частотных характеристик трубопровода с учетом взаимодействия с опорами при различных условиях опирания рассмотрено в / 15, 22, 26/. Величина аэродинамического демпфирования при колебаниях трубопроводов определена в / 18, 26/.
Практические рекомендации по отстройке от вибраций при колебаниях в ветровом потоке приведены в / 15, 18, 22, 26, 29/.
1.2. Расчеты для нестандартных условий
1.2.1. Особенности расчета подземных и надземных трубопроводов, прокладываемых в северных районах.
К основным особенностям проектирования и эксплуатации трубопроводов в северных районах отнесем необходимость учета значительного интервала наружных температур в течение года, сплошное или островное распространение многолетнемерзлых грунтов, высокую влагонасыщенность грунтов, приводящую при растеплении к развитию солифлюкционных процессов. Промерзание водонасыщенных грунтов связано с развитием процессов неоднородного морозного пучения. При сильных морозах грунты подвержены морозобойному растрескиванию, которое приводит к разрушению заглубленных в грунт протяженных конструкций. Вечномерзлые грунты обладают высокой изменчивостью свойств в зависимости от условий эксплуатации. Высокая несущая способность грунта в мерзлом состоянии при растеплении снижается на несколько порядков [ 10, 32].
Общие рекомендации по строительству и эксплуатации трубопроводов в условиях вечной мерзлоты приведены в / 14, 26, 30/. Вопросы теоретического расчета и практические рекомендации по учету морозобойного растрескивания, снижению нагрузок от пучения и ряд других рассмотрены в / 21, 26/.
Выделим два направления рассмотрения вопросов взаимодействия трубопроводов с промерзающим грунтом. Первое направление связано с разработкой методов и средств воздействия на природную среду с целью недопущения или уменьшения негативного воздействия на инженерные сооружения. Указанные средства могут иметь пассивный характер, основанный на требовании максимального сохранения естественного теплового режима грунта и иных показателей при эксплуатации трубопровода (регулировка температуры перекачиваемого продукта до температуры грунта, установка теплозащитных экранов и т. д.). К средствам активного воздействия отнесем, например, метод защиты от пучения трубопроводов, проложенных в пойменных районах / 21, 26/. Он состоит в кратковременной подаче в трубопровод подогретого газа с целью растепления окружающего грунта на глубину, достаточную для самокоррекции положения трубопровода в талом грунте.
Второе направление связано с разработкой расчетных моделей взаимодействия трубопровода с промерзающим грунтом с целью получения прогнозных значений параметров для заданных условий эксплуатации. Разработки этой группы служат теоретической основой для выработки конкретных рекомендаций и технических решений по обеспечению эксплуатационной надежности трубопроводов. Ниже рассмотрены некоторые модели, применяемые при изучении взаимодействия трубопроводов с промерзающим пучинистым грунтом.
При оценке взаимодействия конструкции с пучинистыми грунтами выделяют два подхода. В первом подходе, исходя из принятых расчетных схем, оценивают силы морозного пучения и рассматривают их в качестве контактной нагрузки на трубопровод. Такой подход реализован в / 10/. Во втором случае предполагают заданным профиль грунта, сложившийся в результате пучения. В этом случае воздействие на трубопровод трактуется как кинематическое.
На практике расчет взаимодействия трубопроводов с промерзающим пучинистым грунтом проводят на более простых моделях типа упругих винклеровских моделей, жесткопластических, в предположении о недеформативности мерзлого грунта. В последнем случае решение дает оценку сверху, завышая реальное сопротивление грунта / 2, 27/.
В работах / 26, 28ы/ для грунта принята винклеровская модель с двусторонними связями. Профиль пучинистого грунта задан случайной функцией продольной координаты.
Решения некоторых задач, основанные на представлении трубопровода круговой цилиндрической оболочкой представлены в / 13, 26/.
1.2.2. Подводные трубопроводы
Нормативные методы расчета подводных трубопроводов рассмотрены в / 6, 23/.
Проблема обеспечения устойчивости подводных трубопроводов имеет ряд особенностей по сравнению с трубопроводами, проложенными в обводненных и слабонесущих грунтах / 5/, что связано с большей нестабильностью грунтовых условий.
В / 36, 40/ рассмотрена устойчивость подводных трубопроводов под действием продольных сжимающих напряжений, вызванных температурным перепадом, и поперечных нагрузок, обусловленных положительной плавучестью трубопровода и его взаимодействием с грунтом засыпки. Проведено сравнение решений, полученных в линейной и нелинейной постановке. В / 36/ приведены примеры расчета устойчивости трубопровода по инженерным методикам на основе расчетных норм Голландии.
Транспортировка по подводному трубопроводу газа, имеющего отрицательную температуру, приводит к обмерзанию трубопровода и, как следствие, повышению его плавучести, что является дестабилизирующим фактором. В / 21/ представлена процедура расчета предельной температуры перекачиваемого газа, исходя из требования обеспечения его устойчивого положения, основанная на теплофизическом расчете взаимодействия трубопровода с окружающей средой.
Под действием подводных течений происходит размывка грунтовой насыпи над трубопроводом, приводящая к уменьшению ее несущей способности. В условиях положительной плавучести происходит подвсплытие трубопровода и образование провисших участков / 21, 25, 23/. При неплотном прилегании подводного трубопровода ко дну при наличие течения возможно возникновение колебаний, природа которых аналогична колебаниям надземного трубопровода / 26/. Колебания трубопровода, сопровождающиеся прогрессирующим разрушением грунтовой засыпки, рассмотрены на основе стержневой модели трубопровода.
В связи с прокладкой морских глубоководных трубопроводов возникла проблема обеспечения устойчивости оболочек трубопроводов против смятия под действием большого гидростатического давления / 35, 36, 37, 39, 43/. В начальный момент повреждение возникает в некоторой наиболее нагруженной зоне оболочки. В условиях локального снижения несущей способности трубопровода, вызванного повреждением, и при постоянной интенсивности внешнего воздействия происходит потеря устойчивости оболочки в виде "схлопывания" сечения на участках значительной протяженности. Смятие оболочки сопровождается вторичными повреждениями типа потери устойчивости в продольном направлении в результате изгиба трубопровода, в условиях полного изменения силовой схемы конструкции.
В работе / 43/ смятие оболочки под действием гидростатического давления рассмотрено с учетом фактора времени в динамической постановке, исследована скорость распространения повреждения трубы, проведено сравнение с результатами эксперимента.
1.2.3. Надземные трубопроводы
Эксплуатация трубопроводов в сложных природно-климатических условиях, в частности, в условиях вечной мерзлоты, в зонах пучинистых грунтов привела к необходимости рассмотрения комплексных расчетных схем, учитывающих взаимодействие трубопровода с опорой / 26, 29/. Разрушение, просадка или выпучивание одной или нескольких опор под действием нагрузок, передаваемых от трубопровода, или в результате взаимодействия с грунтом, приводит к увеличению реальной длины пролета и тем самым к снижению собственной частоты трубопровода и возникновению колебаний трубопровода с недопустимой амплитудой. В / 17/ рассмотрена задача расчета колебаний трубопровода с учетом ударного взаимодействия с просевшей промежуточной опорой. Получены оценки контактных усилий в зависимости от жесткости опоры и интенсивности ветрового воздействия.
Список использованных источников
1. Айнбиндер А.Б., Камерштейн А.Г. Расчет магистральных трубопроводов на прочность и устойчивость. М.: Недра. 1982. 341с.
2. Александров П.А., Харионовский В.В. Расчет подземных трубопроводов в условиях пучения грунта //Сб. научи, тр. М.: ВНИИГАЗ. 1986. С. 37-44.
3. Аугусти Г., Баратта А., Кашиати Ф. Вероятностные методы в строительном проектировании. М.: Стройиздат. 1988. 584с.
4. Бородавкин П.П. Механика грунтов в трубопроводном строительстве. М.: Недра. 1986. 224 с.
5. Бородавкин П.П., Березин В.Л. Сооружение магистральных газопроводов. М.: Недра. 1987. 471 с.
6. Бородавкин П.П., Березин В.Л., Шадрин 0. Б. Подводные трубопроводы. М.: Недра. 1983.
7. Виноградов С. В. Расчет подземных труб на прочность. Учебное пособие. М.: МГМИ. 1980. 151 с.
8. Виноградов С. В. Расчет подземных трубопроводов на внешние нагрузки. М.: Стройиздат. 1980. 135с.
9. Гехман А.С., Зайнетдинов X.X. Расчет, конструирование и эксплуатация трубопроводов в сейсмических районах. М.: Стройиздат. 1988. 182 с.
10. Ершов Э. Д. Физико-химия и механика мерзлых пород. М.: МГУ. 1986. 336с.
11. Клейн Г. К. Расчет подземных трубопроводов. М.: Недра. 1969.
12. Клементьев А.Ф. Устойчивость магистральных трубопроводов в сложных условиях. М.: Недра. 1985. 113с.
13. Лобанов Е.В., Силкин В. М., Харионовский В. В. Об устойчивости газопроводов, прокладываемых в статистически неоднородных грунтах // Вопросы транспорта газа. М.: ВНИИгаз. 1985. С. 8-13.
14. Лютов А. В. Инженерные коммуникации на вечномерзлых грунтах. Л.: Стройиздат. 1981. 144с.
15. Методика расчета многопролетных трубопроводов, применительно к промысловым сооружениям на полуострове Ямал. М.: ВНИИгаз. 1988. 37 с.
16. Морозов В. Н. Магистральные трубопроводы в сложных инженерно-геологических условиях. Л.: Недра. 1987. 121 с.
17. Нефедов С. В., Силкин В.М. Колебания надземного трубопровода с учетом контактного взаимодействия с опорой //Проблемы надежности газопроводных конструкций. М.: ВНИИгаз. 1991. С. 68-79.
18. Петров И.П., Спиридонов В.В. Надземная прокладка трубопроводов. М.: Недра.1984.245 с.
19. Расчет заглубленного газопровода с начальными искривлениями оси. /В.Л. Благонадежин. З.Т. Галиуллин, А.А. Пиняев и др. //Вопросы транспорта газа. М.: ВНИИгаз. 1985. С. 188-197.
20. Рекомендации по оценке несущей способности участков газопроводов в непроектном положении. М.: ВНИИгаз. 1986. 43 с.
21. Рекомендации по повышению надежности эксплуатации пойменных и русловых участков подводных переходов газопроводов Соленинское-Мессояха-Норильск. М.: ВНИИгаз. 1987. 47 с.
22. Рекомендации по прочностным расчетам надземных газопроводов. М.: ВНИИгаз. 1988. 46 с.
23. Рекомендации по оценке работоспособности подводных переходов газопроводов при наличии размывов дна. М.: ВНИИгаз. 1995. 40 с.
24. Строительные нормы и правила. СНиП 2.05.06-85 //Магистральные трубопроводы. Нормы проектирования. М.: Стройиздат. 1985.
25. Харионовский В.В., Окопный Ю.А., Радин В.П. Исследование устойчивости подводных переходов газопроводов, имеющих размытые участки //Проблемы надежности газопроводных конструкций. М.: ВНИИгаз. 1991.С. 94-99.
26. Харионовский В. В. Повышение прочности газопроводов в сложных условиях Л.: Недра. 1990. 180с.
27. Харионовский В. В. Напряжения в газопроводе при воздействии пучения грунта // Транспорт природного газа: Сб. науч. тр. /М.: ВНИИгаз. 1984. С.153-159.
28. Харионовский В. В. Анализ надежности северных газопроводов // Надежность газопроводных конструкций: Сб. науч. тр. /М.: ВНИИгаз. 1990. С. 4-11.
29. Харионовский В. В. Конструкции газопроводов в мерзлых грунтах. Обз. информ. Сер.: Транспорт и подземное хранение газа. - М.: ВНИИЭгазпром. 1992. 62 с.
30. Харионовский В. В. , Курганова И. Н. Надежность трубопроводных конструкций. Теория и технические решения. М. - 1995. 125 с.
31. Цейтлин А. И., Бернштейн А. С., Гусева Н.И., Попов Н.А. Новая редакция раздела "Ветровые нагрузки" главы СНиП "Нагрузки и воздействия" //Строительная механика и расчет сооружений. 1987. № 6. С. 28-33.
32. Цытович Н.А. Механика мерзлых грунтов. М.: Высшая школа. 1973. 448 с .
33. Ahmed S., Asce A.M., McMickle R.W. Soil-pipe interaction and pipeline design // Transp. Engn. J., Trans. ASCE. 1981. V. 107. N TEI. P. 45-58.
34. Audibert J.M.E., Nyman K.J. Soil restraint against horizontal motion of pipes //J. Geotech. Engn. Div., Trans. ASCE. 1977. V. 103. N GTIO. P. 1119-1142.
35. Bruschi R., Curti G., Vitali L. The crumpling strength of tubulars: application to offshore pipelines // Proc. of the 9th Int. Conf. on Offshore Mechanics and Arctic Engineering / Ed. S.T. Barras and all./ASME. New York. 1990. V. 5. P. 189-198.
36. Gresnigt A., Van Foeken R. Strength and deformation capacity of pipelines loaded by local loads and bending // Pipeline Technology Conference. Ostende. 1990 / Ed. R. Dennis. Part B. Antwerpen: K.VIV. 1990. P. 12.21-12.31.
37. Kamalarasa S., Calladine C.R. Buckle propagation in submarine pipeline // Int. J. Mech. Sci. 1988. V. 30. N 3/4. Р . 217-228.
38. Larghamee M., Tigue D.B. Soil-structure interaction of flexible pipe under pressure//Transportation Research Record. 1986. № 1087. P. 46-53.
39. Palmer А . С ., Martin J.H. Buckle propagation in submarine pipelines // Nature. 1985. V. 254. N 6. Р . 46-48.
40. Pedersen Т . Р ., Michelsen J. Large deflection upheaval buckling of marine pipelines // Report № 370. Lyngby: Technical University of Denmark. 1988. 21 p.
41. Peng L.-Ch. Stress analysis methods for underground pipelines (Part I -Basic calculation) // Int. Pipe Line Industry. 1978. V. 48. N 4. Р . 67-72.
42. Peng L.-Ch. Stress analysis methods for underground pipelines (Part 2 -Soil-pipe interaction) // Int. Pipe Line Industry. 1978. V. 48. N 5. Р . 65-74.
43. Song H.-W., Tassoulas J.L. Dynamics of propagating in deep-water pipelines // The 10th Int. Conf. OMAE. Stavanger. Norway. June 23-28, 1991. Vol. V.P.I 87-192.
44. Vinogradov A.M. Nonlinear buckling analysis of pipelines subjected to creep of supporting soil // J. Press. Ves. Techn., Trans. ASME. 1989. V. III. N 2. P . 191-196.
2. КОММЕНТАРИЙ К П. 3.3 . КЛАССИФИКАЦИЯ ОТКАЗОВ И ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
2.1. Критерии разрушения элементов трубопроводных конструкций при статическом нагружении
Известно / 1, 2/, что характеристики пластичности и хрупкости материала зависят от условий работы. Поэтому следует говорить не о хрупком и пластичном материале, а о хрупком и пластичном состояниях материала.
Для описания условий разрушения материалов в хрупком состоянии применяют критериальные соотношения первой и второй теорий прочности, а для пластических состояний используют третью и четвертую теории прочности. Все четыре теории прочности предназначены для описания состояния материала в точке и имеют смысл локальных критериев разрушения.
Для систематизации и наглядности применения различных теорий прочности в работе / 2/ была предложена диаграмма механического состояния (ДМС) материала. На диаграмме по оси абсцисс наносят рассчитанные на основе второй теории прочности приведенные напряжения растяжения S пр для данного напряженного состояния, по оси ординат t max - наибольшие приведенные касательные напряжения, полученные с использованием третьей теории прочности. Луч, соединяющий полученную точку с началом координат, характеризует жесткость данного напряженного состояния. Чем больше угол наклона ( a = arctg ( t max / S пр )), тем мягче способ нагружения и меньше стеснение деформаций. Нагружение по лучу может вызвать разрушение по механизму отрыва, если Sпр= S от или по механизму среза, если t max = t k . Здесь t k - истинное касательное напряжение в момент окончательного разрушения по механизму среза (сопротивление срезу); S от - истинное сопротивление отрыву. В зависимости от типа напряженного состояния возможна реализация различных промежуточных вариантов деформирования и разрушения.
В / 3/ был разработан, а в работах / 4, 5/ получил дальнейшее развитие более общий локальный критерий разрушения, основанный на доказанном факте инвариантности предельного сопротивления отрыву материала S от температуре и жесткости напряженного состояния. В качестве физической основы критерия приняты микроструктурные механизмы разрушения. Хрупкое разрушение рассмотрено как результат зарождения и развития острых микротрещин, вязкое - как результат образования, развития и слияния микропор.
Критерий хрупкого разрушения имеет вид
s i ³ s Т ( Т ), (1)
s i ³ S отр (e1), (2)
где s i - интенсивность пластических напряжений, s Т (Т) - зависимость напряжения текучести от температуры, s i - первое главное напряжение, S отр ( e 1 ) - зависимость истинного разрушающего напряжения Sk в опытах на растяжение (цилиндрические образцы) от величины истинной предельной деформации ер при реализации разрушения отрывом. Условие (1) представляет собой условие зарождения микротрещин, условие (2) - условие их развития. Критерий вязкого разрушения запишем в виде
е i ³ е kp , (3)
где е i - интенсивность пластических деформаций, ekp - характерная для данного материала величина, практически не зависящая от температуры.
Для реализации критерия необходимы результаты серийных испытаний по разрушению гладких цилиндрических образцов при разных температурах.
Для расчета трубопроводов с локальными дефектами преобразуем критерий ( 1) - ( 3) к виду
s i ³ s Т ( Т ), (4)
s i ³ S отр (e1),
s i ³ s кр , (5)
где ( 4) представляет собой критерий хрупкого разрушения, а ( 5) .-определяет вязкое разрушение. Критерий (4), ( 5) дает возможность использовать преимущества ДНС, сохраняя способность критерия (1) - (3) получать результаты в широком интервале температур. Константы, входящие в ( 4), ( 5), определяются из эксперимента по разрушению растяжением стандартных гладких цилиндрических образцов в интервале температур -20 - +20 °С.
Список использованных источников
1. Давиденков Н.Н. Динамическая прочность и хрупкость металлов. К.: Наукова думка, 1981. - 704 с.
2. Фридман Я.Б. Механические свойства металлов. М.: Машиностроение, 1974. - T . I .- 472 с.
3. Копельман Л.А. Сопротивляемость сварных узлов хрупкому разрушению. М.: Машиностроение, 1978. - 232 с.
4. Карзов Г.П. , Марголин Б.З. , Швецова В. А. Физико-механическое моделирование процессов разрушения. Спб.: Политехника, 1993.- 391 с.
5. Марголин Б.З., Костылев В.А. Критерий хрупкого разрушения: структурно-механический подход // Проблемы прочности. 1992. № 2.-С. 3-16.
2.2. Критерии прочности и методы расчета элементов трубопроводов при малоцикловом нагружении
В общей системе прочностных расчетов газопроводных конструкций вопросы малоцикловой прочности принадлежат к группе поверочных расчетов. При определении несущей способности и долговечности по критериям малоцикловой прочности необходимо учитывать всю систему силовых, кинематических и температурных воздействий за период фактической эксплуатации.
Основные элементы трубопроводных конструкций работают при номинальных напряжениях ниже пределов текучести. Наступление предельных состояний по критериям малоцикловой прочности может произойти, как правило, в зонах с локальной концентрацией напряжений. Зоны концентрации сосредоточены в местах изменения геометрии конструкции, на участках с локальной неоднородностью свойств материала и вблизи дефектов различной природы. Поэтому главное внимание при оценке НДС трубопровода должно быть направлено на выявление зон концентрации и изучение режимов локального деформирования.
Режимы локального деформирования должны быть изучены и описаны с учетом кинетики деформаций и характера изменения свойств материала при циклическом деформировании / 1, 5/.
В теории малоцикловой прочности применяют критерии трех групп: деформационные, энергетические и критерии, основанные на учете поврежденности материала. Неединообразие критериев, применяемых в теории малоцикловой прочности, отражает сложность и неоднозначность процессов малоциклового деформирования.
Кратко рассмотрим основные типы критериев, применяемых при малоцикловом нагружении.
Важную группу составляют критерии, основанные на энергетической концепции условий образования предельного состояния. Исследования малоцикловой прочности с энергетических позиций состоит в определении критического значения накопленной при деформировании энергии или той ее части, что пошла на разрушение материала, и установлении связи критической характеристики с показателями энергии деформирования при статическом разрушении. Конкретная форма представления критериальных уравнений зависит от положенных в основание теории гипотез / 5/. Наиболее широкое распространение получили деформационно-кинетические критерии малоциклового разрушения / 2/. В соответствии с ними разрушение наступает тогда, когда односторонне накопленная пластическая деформация или циклическая упругопластическая деформация, или их комбинация достигнет предельного значения. Для учета суммарного повреждения от разных типов деформирования применяют правило линейного суммирования повреждений.
В ряде методик, например / 3/, реализована концепция иерархической системы расчетных методик. В зависимости от уровня располагаемой исходной информации, требований к точности оценок применяются различные по сложности процедуры расчетной оценки малоцикловой прочности и долговечности. Упрощенные методики / 4/ используют только стандартные данные о физико-механических материалах. Для более точного расчета предполагается проведение дополнительных экспериментальных исследований и применение более сложных расчетных процедур. Такой подход представляется наиболее перспективным при разработке методических рекомендаций для расчета показателей прочности и долговечности трубопроводных конструкций с поверхностными дефектами.
Список использованных источников
1. Гусенков А. П. Свойства диаграмм циклического деформирования при нормальных температурах // В кн.: Сопротивление деформированию и разрушению при малом числе циклов нагружения. М.: Наука, 1967. - С. 34-63.
2. Махутов Н. А. Деформационные критерии разрушения и расчет элементов конструкций на прочность. М.: Машиностроение, 1981. - 272 с.
3. Методические указания. Алгоритмы и структура программного обеспечения расчетов на прочность элементов конструкций при циклическом нагружении на ПЭВМ. М.: МЦНТИ, МНТК "Надежность машин", 1991. - 72 с.
4. Методические указания. Расчеты прочности элементов конструкций при малоцикловом нагружении. М.: МЦНТИ, МНТК "Надежность машин", 1987. - 41 с.
5. Сопротивление материалов деформированию и разрушению / Справочное пособие. Ч. 2. Под ред. В. Т. Трощенко. К.: Наукова думка, 1994. - 701 с.
2.3. Критерии прочности и методы расчета элементов трубопроводов при много цикловом нагружении
В данном разделе приведем некоторые дополнительные рекомендации по оценке усталостной долговечности в многоцикловой области (общее число циклов нагружения превышает 105) по критерию образования усталостной трещины. Применительно к трубопроводам такие расчеты могут иметь самостоятельное значение или могут быть использованы для оценки продолжительности стадии зарождения усталостных трещин с последующим применением методов механики разрушения для расчета долговечности и ресурса по критериям роста усталостных трещин.
Методы расчета деталей машин и конструкций на выносливость хорошо разработаны и широко применяются в самых различных областях промышленности и строительства. Обоснование базовых методик и вывод формул даны в работах / 1, 2, 3/.
На основе базовых методов разработаны проблемно-ориентированные методические рекомендации практического характера для различных отраслей промышленности и строительства. Приведем примеры некоторых методических разработок.
В работе / 4/ приведены рекомендации по расчету деталей машин на выносливость с вероятностной природой нагрузок и воздействий и свойств материалов. В методических рекомендациях отражены вопросы оценки функции распределения ресурса деталей машин на основе исходной информации об эксплуатационной нагруженности и характеристиках сопротивления усталости, а также методах определения характеристик сопротивления усталости.
В работе / 5/ рассмотрены методы формирования обобщенных спектров нагружения элементов машин и конструкций при расчетах и испытаниях на усталость. Применение данной методики необходимо при расчетах и испытаниях изделий под действием нагрузок и воздействий, случайным образом изменяющихся во времени.
Особенности применения методов расчета на выносливость сварных соединений рассмотрены в работе / 6/. В методике отражены два блока вопросов, связанных с расчетно-экспериментальными методами оценки сопротивления усталости сварных соединений и вероятностными методами расчета на усталость сварных конструкций.
Базовые методы расчетов на выносливость носят в целом универсальный характер и могут быть достаточно легко адаптированы для применения при расчетах сопротивления усталости трубопроводных конструкций.
Список использованных источников
1. Когаев В.П. Определение надежности механических систем по условию прочности. М.: Знание. 1976. Вып. 1: 48 с. Вып. 2: 48 с.
2. Когаев В.П. Расчеты на прочность при напряжениях, переменных во времени. М.: Машиностроение. 1977. - 232 с.
3. Серенсен С.В., Когаев В.П., Шнейдерович P . M . Несущая способность и расчеты на прочность деталей машин. М.: Машиностроение. 1975. 488 с.
4. Методические указания. Расчеты деталей машин на выносливость в вероятностном аспекте. М.: МЦНТИ, МНТК "Надежность машин". 1991. - 85 с.
5. Методические указания. Формирование информации о нагруженности в эксплуатации и оценка долговечности деталей машин. М.: МЦНТИ, МНТК "Надежность машин". 1991. - 116 с.
6. Методические указания. Вероятностный подход к расчетам сварных конструкций на усталость. М.: МЦНТИ, МНТК "Надежность машин". 1993. - 103 с.
2.4. Критерии трещиностойкости элементов трубопроводов по отношению к усталостным трещинам
В принципе, наличие несквозных трещин в трубопроводах является неизбежным даже при самой тщательной системе приемочного и промежуточного контролей. Цель расчета по критериям трещиностойкости состоит в том, чтобы не допустить прорастания начальных и приобретенных дефектов до состояния, когда герметичность будет нарушена.
Будем различать три критерия трещиностойкости.
Первый критерий - отсутствие страгивания трещин. Для того чтобы существующая трещина начала продвигаться вперед необходимо, чтобы размах D К коэффициента интенсивности напряжений К у фронта этой трещины превысил некоторое значение Kth , зависящее от свойств материала в рассматриваемый момент времени. Методы расчета коэффициентов интенсивности напряжений для поверхностных полуэллиптических трещин в сосудах давления и трубопроводах рассмотрены в приложении 2.
Пороговое значение Kth , как правило, составляет величину порядка нескольких процентов от основной характеристики трещиностойкости материала - критического коэффициента интенсивности Кс.
Второй критерий - собственно критерий герметичности, который заключается в условии непрорастания начального дефекта до некоторого допустимого размера (например, недопущение сквозного прорастания трещины) за рассматриваемый период эксплуатации. Расчет по этому критерию требует решения уравнений роста усталостных трещин ( см. приложение 2).
Третий критерий - критерий устойчивости по Гриффитсу. Для того чтобы трещина начала развиваться неустойчиво, т.е. практически в динамическом режиме, необходимо нарушение одного из неравенств типа
(K1a/K1c)2+(K2a/K11c)2 £ 1
(K1b/K1b)2+(K2b/K11b)2 £ 1
Дополнительные пояснения приведены в разделе 2.3.6 приложения 2. Меры борьбы с этим явлением заключаются, как правило, в выборе достаточно высоких коэффициентов запаса прочности при проектировании конструкции.
Список использованных источников
1. Болотин В.В. Уравнения роста усталостных трещин //Механика твердого тела. 1983. №4. С. 153-160.
3. КОММЕНТАРИЙ К П. 3.4 . ТРЕБОВАНИЯ К ПОСТРОЕНИЮ РАСЧЕТНЫХ СХЕМ ДЛЯ ОЦЕНКИ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ УЧАСТКА ГАЗОПРОВОДА
Рассмотрим обобщенный алгоритм, реализующий основные подходы к решению задачи по обеспечению статической прочности трубопроводных конструкций, содержащих локальные дефекты. Структурная схема алгоритма приведена на рис. 3.1. Предлагаемый расчет относится к категории поверочных прочностных расчетов, используемых для оценки работоспособности трубопроводной системы, в том числе, с учетом локальных дефектов. Алгоритм рассчитан на применение современной вычислительной техники. Кратко остановимся на основных элементах предлагаемого алгоритма.
Элементы 1, 2, 3, 4 алгоритма относятся к этапу сбора и подготовки необходимой для расчета исходной информации и отвечают четырем типам требуемых данных.
Элементы 1, 2. Пространственная конфигурация исследуемого участка трубопровода (проектное решение, конфигурация при укладке и на момент исследования). Достаточно полно должны быть отмечены конструктивные особенности изготовления и прокладки трубопровода (наличие прямолинейных, упругоискривленных, криволинейных из гнутых труб участков, конструкция и расположение пригрузов и анкерных устройств, особенности грунта, вид прокладки и т.д.). При необходимости оценки дефектов сварного шва требуется дополнительная информация о технических особенностях и технологии производства сварочных работ.
Элемент 3. Нагрузки и воздействия согласно приводимым в настоящем документе рекомендациям. При статическом расчете следует учитывать нагрузки, время приложения или изменения которых велико по сравнению с периодом собственных упругих колебаний конструкции. При статическом учете нагрузок, изменяющихся во времени, следует использовать их максимальные значения.
Элемент 4. Минимально необходимыми характеристиками материала для первого этапа расчета являются стандартные механические и прочностные свойства материала. В ряде случаев требуется полная диаграмма растяжения и характеристики сварного соединения / 2/.
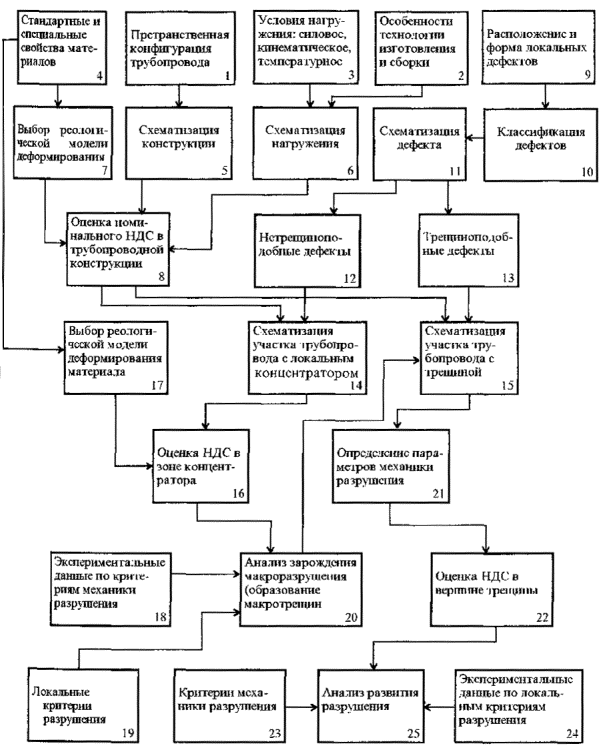
Рис. 3.1. Оценка статической прочности трубопроводной конструкции с дефектом
Элементы 5, 6, 7 алгоритма относятся к этапу построения расчетной механо-математической модели. Для схематизации конструкции в большинстве случаев подходит стержневая аппроксимация. Для участков трубопровода с большой кривизной может потребоваться усложнение модели учетом оболочечных эффектов. Схематизация нагрузки заключается в задании распределения по длине трубопровода силового, кинематического и температурного воздействия. Выбор реологической модели деформирования определяется сравнением проектной пространственной конфигурации исследуемого участка трубопровода с конфигурацией, имеющейся на момент исследования. Необходимость учета пластических деформаций требует выбора соответствующей реологической модели (в этом случае требуется, как минимум, полная диаграмма деформирования материала).
Элемент 8. Оценка номинального напряженно-деформированного состояния (НДС) трубопроводной конструкции может проводиться любым из приемлемых машинно-ориентированных методов расчета (метод конечных элементов, различные формализованные модификации метода начальных параметров, метода прогонки, метода перемещений, смешанных методов). В простейших случаях возможен ручной расчет классическими методами строительной механики. В ряде случаев необходим учет больших перемещений. Номинальные НДС определяются для наиболее напряженных участков исследуемого трубопровода. В случае невыполнения регламентируемых нормами условий требуется принятие конструктивных решений по устранению перенапряжения участков исследуемого трубопровода. Возможные варианты решений должны быть соответствующим образом просчитаны.
Элементы 9-13. Информация о возможных дефектах на проектируемых трубопроводах получается из статистических данных эксплуатируемых газопроводов. Все локальные дефекты следует разбить на три группы: компактные геометрические несовершенства, внутренние дефекты в стенке трубопровода и поверхностные дефекты, расположенные на внутренней или внешней поверхностях трубопровода. Схематизация дефекта должна подчиняться принципу разумной консервативности: дефекты-аналоги должны давать гарантированно заниженные значения прочности и долговечности, но запас не должен быть слишком велик. Наиболее простым способом консервативной схематизации является замена любых несплошностей (трещины, поры, включения, непровары, надрезы и т.д.) трещинами, которые являются наиболее опасным видом дефектов. Этот способ удобен, поскольку требует минимума информации о дефекте.
Дефекты по степени создаваемой ими концентрации напряжений делятся на трещиноподобные и нетрещиноподобные. Все дефекты из подгруппы геометрических несовершенств автоматически попадают в группу нетрещиноподобных дефектов. Поверхностные и внутренние несплошности в зависимости от полноты информации об их геометрии и характере этой геометрии будем делить на трещиноподобные и нетрещиноподобные. При неполноте информации о дефекте наиболее целесообразно использовать аппроксимацию эллиптической или полуэллиптической трещиной. Редуцирование групповых дефектов такой формы позволяет существенно упростить расчетную схему.
Менее консервативная оценка может быть получена для дефекта, создающего конечную концентрацию напряжений, и пространственная конфигурация которого известна с высокой точностью (например, пологая каверна на внешней поверхности трубопровода). Такой дефект называется нетрещинообразным и может быть схематизирован гладким пространственным концентратором-аналогом, обладающим несколько более высоким коэффициентом концентрации (по сравнению с дефектом-оригиналом). Для поверхностных дефектов используется полуэллипсоидальный концентратор. Таким образом все имеющиеся дефекты схематизируются либо трещиной, либо концентратором определенного вида.
Элементы 14, 15. В зависимости от схематизации дефектов (трещина или концентратор) для дальнейшего расчета используется специальная программа для локального участка трубопровода с эквивалентным дефектом.
Элементы 16-17. Оценка НДС в зоне локализации нетрещиноподобного дефекта представляет собой отдельную, весьма сложную задачу и требует применения специальных программ. Современные пакеты прикладных программ позволяют определять НДС в полной трехмерной постановке, учитывающей упругопластическое деформирование материала в зоне концентрации напряжений. При этом реальный дефект может быть аппроксимирован расчетным, геометрически подобным дефектом, вообще говоря, с любой требуемой степенью точности. Естественные ограничения глубины детализации расчетной схемы определяются возможностями выбранного пакета программ и техническими характеристиками ЭВМ.
В ряде случаев, особенно для дефектов из подгруппы компактные геометрические несовершенства, решение может быть получено менее трудоемкими методами. Решение в этих случаях строится в оболочечном приближении в рамках деформационной теории пластичности.
Еще один путь упрощения задачи состоит в приближенной оценке пластического решения по полям напряжений, полученным в линейной постановке. Наиболее часто для этих целей используют формулу Нейбера / 4/ и различные варианты ее модификаций. Применение этого приема позволяет по упругому решению (теоретическим коэффициентам концентрации) и обобщенной кривой деформирования получить достаточно качественную оценку для пластических коэффициентов концентрации напряжений и деформаций в зоне концентрации, вызванной наличием дефекта. Часто этого оказывается достаточно для оценки прочности и долговечности конструкции.
Элементы 18, 19, 20 алгоритма соответствуют этапу анализа на основе локальных критериев разрушения процесса зарождения макроразрушения в высоконагруженной зоне у вершины концентратора. Невыполнение условия локального разрушения свидетельствует о неопасности рассматриваемого локального дефекта с точки зрения статической прочности конструкции. Если же локальные критерии разрушения констатируют инициализацию макроразрушения, то в зоне концентратора образуется вязкая или хрупкая трещина, которая требует схематизации ( элемент 15 алгоритма) и дальнейшего анализа ее развития ( элементы 16-20).
Элементы 21-25 относятся к этапу расчета прочности трубопровода по критериям механики разрушения. Применение этих критериев состоит в оценке параметров механики разрушения и сопоставлении их с критическими экспериментальными значениями. Необходимые параметры механики разрушения в большинстве случаев могут быть найдены по известным аппроксимационным формулам / 5/, либо должны быть получены численно / 6/. Выполнение условия устойчивости для эквивалентной трещины свидетельствует о некритичности данного трещиноподобного дефекта при статическом нагружении. Практически это означает, что рассматриваемый трещиноподобный дефект (группа дефектов) при заданном уровне статического нагружения не вызовет катастрофического распространения магистральной трещины. В противном случае исследуемый локальный дефект следует считать опасным и требуются конструктивные мероприятия по его устранению.
Список использованных источников
1. СНиП 2.05.06-85. Магистральные трубопроводы. Нормы проектирования. М.: Стандарты, 1985. - 52 с.
2. Карзов Г. П. , Марголин Б. 3. , Швецова В. А. Физико-механическое моделирование процессов разрушения. Спб.: Политехника, 1993. - 391 с.
3. ASME Boiler and Pressure Vessel Code: Sect. II. New York, 1986.- 558 p.
4. Балина B . C ., Мадьякшас Г.Г. Прочность, долговечность и трещиностойкость конструкций при длительном циклическом нагружении. СПб: Политехника, 1994. - 204 с.
5. Справочник по коэффициентам интенсивности напряжений. В 2-х томах/Под ред. Ю.Мураками. М.: Мир, 1990. Т. 1. - 448 с.; Т. 2. - С.448-1016.
6. Вычислительные методы в механике разрушения /Под ред. С. Атлури. М.: Мир. 1990. - 392 с.
4. КОММЕНТАРИЙ К П. 3.5 . ФОРМИРОВАНИЕ РАСЧЕТНЫХ УЧАСТКОВ
В комментарий к п. 3.5 включена расширенная версия подразделов 3.5.8-3.5.11, изложенная на частном примере формирования расчетных участков для надземного трубопровода, проложенного на свайном основании при просадке одной из промежуточных опор.
На основе анализа конструктивной схемы трубопровода, данных о нагрузках и воздействиях на него, разобьем трассу трубопровода на расчетные участки.
Будем различать два уровня разбиений конструкции на расчетные участки. Первый - соответствует разбиению конструкции на элементы в соответствии с выбранными при оценке напряженно-деформированного состояния расчетными схемами. Так в качестве основной расчетной схемы надземного трубопровода может быть принята модель многопролетного стержня кольцевого поперечного очертания, размещенного на жестких или упругоподатливых опорах. В этом случае длина расчетного участка, как правило, не должна превышать длину участка трубопровода, расположенного в пределах одного температурного блока между двумя "мертвыми" опорами, поскольку при определении величины продольного усилия, действующего в трубопроводе, необходимо учитывать взаимодействие и взаимовлияние конструктивных элементов в пределах температурного блока. В то же время при известном продольном усилии расчет колебательных режимов трубопровода может быть проведен по иным схемам, в соответствие с которыми изменится вид расчетного участка.
Цель разбиений второго уровня состоит в выделении участков с однородными характеристиками по выбранной группе параметров. Перечень параметров, учитываемых при разбиении, зависит от характеристик конструкции, вида предполагаемых расчетов, типов возможных отказов и предельных состояний, реализуемых на выделенном расчетном участке. При этом вначале формируют перечень типов расчетных участков, объединенных заданными общими признаками.
Учитывая общий характер нагрузок, действующих на надземный газопровод, и распределение дефектов в теле трубы, выделим следующие возможные группы расчетных участков.
Примем в качестве первой расчетной области элемент оболочки мерой L 0 с наибольшим уровнем контактных напряжений. В первом приближении аппроксимируем область L о цилиндрической панелью радиуса R , равным радиусу срединной поверхности оболочки. Размеры области в продольном 21х и поперечном 21ху направлениях определяются масштабом неоднородности напряженного состояния в оболочке газопровода в зоне опирания на опору.
В зависимости от режима нагружения наибольший уровень напряжений в надземном трубопроводе наблюдается в сечениях над опорами, либо в центральной части пролета. Учитывая, что характерный масштаб неоднородности изгибных напряжений в пролете сравним с длиной пролета, в качестве расчетного примем участок газопровода, заключенный между опорами. При этом полагаем, что во всех сечениях расчетного участка действуют напряжения максимальной в пределах участка интенсивности. Для учета неоднородности напряжений в продольном направлении, участок трубопровода между опорами необходимо разбить на более короткие элементы, с меньшим уровнем напряжений. Дополнительное разбиение приводит к существенному увеличению объема вычислений. Естественным ограничением при этом является неустранимая погрешность исходных данных о свойствах конструкции и действующих на нее нагрузок. Поэтому используемые расчетные схемы и способ формирования расчетных участков должны соответствовать уровню, объему и степени достоверности исходной информации.
Полагаем, что на расчетных участках первых двух типов рост трещин происходит как в продольном, так и поперечном направлениях.
В качестве расчетного участка третьего типа примем элемент оболочки, содержащий сварные швы. Необходимость выделения сварных швов обусловлена различием физико-механических свойств и уровня дефектности основного металла и материала в области шва. В качестве меры расчетной области примем длину сварного шва. Полагаем, что развитие трещиноподобных дефектов происходит только в направлении продольной оси сварного шва.
При оценке надежности под длиной расчетного участка понимается общая протяженность перечисленных эталонных расчетных участков отдельно по каждому из трех типов. При этом уровни напряжений и параметры начальной дефектности принимаем равными соответствующим максимальным значениям, определенным на всей совокупности расчетных участков.
В приложении 2 приведен пример расчетного прогнозирования показателей конструктивной надежности надземного газопровода по критерию роста усталостных трещин с использованием предлагаемой методики выделения расчетных участков.
5. КОММЕНТАРИЙ К П. 3.6. ФОРМИРОВАНИЕ ПРОСТРАНСТВА СОСТОЯНИЙ РАСЧЕТНОГО УЧАСТКА
Процедура формирования пространства состояний расчетного участка подробно прокомментирована в приложениях 2 и 3.
В первом случае приведен пример формирования пространства состояний для участка надземного трубопровода, проложенного на опорах при оценке показателей конструктивной надежности в случае контактного взаимодействия трубопровода с просевшей промежуточной опорой.
В приложении 3 рассмотрены общие подходы к выбору перечня характеристических параметров, определению соответствующих парциальных вероятностей в случае независимых и взаимозависимых характеристических параметров. В приложении приведен пример формирования пространства состояний для частного случая трубопровода, взаимодействующего с единичным бугром пучинистого грунта.
6. КОММЕНТАРИЙ К П. 3.8 . МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
6.1. Применение вероятностных моделей при расчете трубопроводов
По отношению к трубопроводам проблема надежности может быть условно разделена на два блока. В первый блок включены вопросы обеспечения системной надежности транспорта газа. Во вторую группу входят вопросы обеспечения конструктивной надежности механических систем, в частности, линейных частей трубопроводов, составляющих трубопровод в целом.
Характерным примером решения задач первой группы является работа / 8/, в которой дано описание трубопровода как сложной резервируемой и управляемой системы.
Методы оценки показателей надежности механических систем различного назначения подробно рассмотрены в монографиях / 2, 3, 4/.
В зависимости от исходных посылок оценка конструкционной надежности механических систем может быть проведена различными методами. Для статических моделей характерно задание условия надежности в виде ограничений на предельную величину характеристических параметров или некоторой функции этих параметров, задаваемых исходя из критериев обеспечения прочности, устойчивости, герметичности т.д. При этом характеристические параметры полагают случайными величинами. Статические модели рассмотрены в работах / 1, 5, 6/. В них приведены наиболее распространенные типы вероятностных распределений различных характеристических параметров. Пример расчета трубопроводов по заданной мере надежности на основе статической модели приведен в работе / 5/.
Следующую группу составляют модели, в которых состояние трубопровода охарактеризовано некоторым вектором качества, компоненты которого - случайные функции времени и, в общем случае, пространственных координат. Надежность системы определяют через вероятность пребывания вектора качества в пределах допускаемой области в течение всего срока эксплуатации / 2, 9, 10/.
Форма представления вектора качества, конфигурация и размеры допускаемой области зависят от принятой модели расчета / 7, 10, 11/.
Если для отказов в трубопроводе применима пуассоновская модель, то надежность системы можно задать через параметр интенсивности отказов, в общем случае зависящий от времени и пространственной координаты. Большинство практических расчетов основано на применении пуассоновских моделей / 9, 10/.
Прежде всего, вероятностные модели могут быть рекомендованы для оценки показателей надежности трубопроводов, эксплуатируемых в сложных природно-климатических условиях. Ниже приведены некоторые варианты применения вероятностных моделей для расчета показателей надежности трубопроводов с учетом взаимодействия с грунтом.
Задача об изгибе балки, лежащей на сплошном упругом основании винклеровского типа со случайными свойствами, включая экспериментальные исследования свойств грунтовых оснований, сопоставление теоретических и экспериментальных результатов, представлена в / 9/.
В / 10/ на основе экспериментальных данных оценена плотность распределения вероятности характеристических параметров пучения, а на их основе - плотность распределения изгибающих моментов в трубопроводе при взаимодействии с пучинистным грунтом. В результате получены оценки среднего срока службы трубопровода и оценки показателей надежности в зависимости от уровня пучения. Различные аспекты данной задачи подробно рассмотрены в приложениях 1- 4.
Оценка показателей надежности трубопроводных конструкций по отношению к принятой системе предельных состояний не является, как правило, конечной целью расчета. В условиях недостаточной и не вполне достоверной информации о действительных условиях эксплуатации конструкции и ее свойствах, сравнение численных значений показателей надежности нескольких возможных вариантов - один из наиболее корректных способов выбора наиболее оптимального решения. В этих условиях важны не конкретные абсолютные значения показателей надежности, а соотношение показателей, полученных для рассматриваемых вариантов.
Список использованных источников
1. Аугусти Г., Баратта А., Кашиати Ф. Вероятностные методы в строительном проектировании. М.: Стройиздат. 1988. 584 с.
2. Болотин В.В. Методы теории вероятностей и теории надежности в расчетах сооружений. М.: Стройиздат. 1981. 351 с.
3. Болотин В.В. Прогнозирование ресурса машин и конструкций. М.: Машиностроение. 1984. 312с.
4. Болотин В.В. Ресурс машин и конструкций. М. : Машиностроение. 1990. 480 с.
5. Бородавкин П.П. , Березин В.Л. Сооружение магистральных газопроводов. М,: Недра.1987.471 с.
6. Капур К., Ламберсон Л. Надежность и проектирование систем. М.: Мир. 1980. 604 с.
7. Лобанов Е.В. , Силкин В.М. , Харионовский В. В. Об устойчивости газопроводов, прокладываемых в статистически неоднородных грунтах // Вопросы транспорта газа. М.: ВНИИгаз. 1985. С. 8-13.
ы8. Ставровский Е.Р. , Сухарев М.Г. , Карасевич А.М. Методы расчета надежности магистральных газопроводов. Новосибирск. Наука. 1982. 125 с.
9. Харионовский В.В. Повышение прочности газопроводов в сложных условиях Л.: Недра. 1990. 180 с.
10. Харионовский В.В. Анализ надежности северных газопроводов // Надежность газопроводных конструкций: Сб. науч. тр. / М.: ВНИИгаз. 1990. С . 4-11.
11. Fearnehough G.D. Pipeline safety // Pipeline Technology Conference. Ostende. 1990/Ed. R.Dennis. Part. B. Antwer-pen: K.VIV. 1990. P . 10.1-10.8.
6.2. Применение вероятностных моделей для оценки показателей надежности трубопроводов по критерию трещиностойкости. Последовательность выполнения расчетов
В приложении 2 рассмотрена процедура расчета показателей надежности надземного трубопровода по критерию роста усталостных трещин. Представленная там методика расчета применима и легко может быть адаптирована к широкому классу задач исследования надежности трубопроводных систем. Ниже приведена общая детализированная последовательность проведения расчетов по указанной методике, согласованная с рекомендациями раздела 3.8.
6.2.1. Формирование исходных данных:
6.2.1.1. Формирование расчетных участков ЛЧМГ D Li ;
6.2.1.2. Формирование классов по расчетным участкам Ф ij ;
6.2.1.3. Задание геометрических и прочностных характеристик (для участка трубопровода или для всей трассы в целом в зависимости от однородности типа и геометрии труб);
6.2.1.4. Задание параметров трещиностойкости и уровней начальной дефектности на каждом из участков;
6.2.1.5. Задание параметров вероятностных распределений для начальных размеров дефектов;
6.2.2. Формирование нагрузок и воздействий, реализуемых в данном классе Ф ij :
6.2.2.1. Постоянно действующие нагрузки и воздействия по сезонам;
6. 2. 2. 2. Непроектные нагрузки и воздействия по сезонам;
6.2.2.3. Формирование реализации (серии реализации) нагрузок и воздействий в течение исследуемого календарного периода эксплуатации;
6.2.3. Задание (вычисление) вероятностей реализации событий данного класса Hij (Ф ij ):
6.2.4. Расчет напряженно-деформированного состояния для каждого участка трубопровода при нагрузках и воздействиях заданного класса;
6.2.4.1. Вычисление перемещений участка трубопровода;
6.2.4.2. Вычисление напряжений в окрестности трещины за исследуемый календарный период эксплуатации;
6.2.4.3. Выделение квазистатических и циклических составляющих напряжений в окрестности дефекта;
6.2.5. Моделирование роста усталостных трещин для каждого расчетного участка трубопровода при сформированных для данного класса полях напряжений в окрестности дефекта и вычисление границ допустимых областей начальных размеров трещин по критериям герметичности и устойчивости трещин;
6.2.6. Исследование вероятности потери герметичности данного расчетного участка при фиксированном классе нагрузок и воздействий за исследуемый эксплуатационный период:
6.2.6.1. Моделирование псевдослучайной выборки начальных размеров трещин;
6.2.6.2. Цензурирование выборки по принадлежности допустимой области;
6.2.6.3. Выделение из цензурированной выборки трещины с наибольшей начальной глубиной;
6.2.6.4. Повторение процедуры
6.2.6.1- 6.2.6.3 и формирование псевдослучайной выборки экстремальных трещин;
6.2.6.5. Моделирование роста трещин данной выборки и формирование выборки экстремальных времен разгерметизации участка;
6.2.6.6. Вычисление методом наибольшего правдоподобия оценок параметров экстремального распределения времени до разгерметизации;
6.2.6.7. Оценка вероятности разгерметизации участка трубопровода за исследуемый календарный срок эксплуатации;
6.2.7. Вычисление показателей надежности и долговечности для участка трубопровода по совокупности классов, сформированной для данного участка;
6.2.8. Оценка полного конструкционного риска и (или) среднего (гамма-процентного) срока службы всей трассы ЛЧМГ.
Этапы 6.2.1- 6.2.4 входят в большинство расчетных и расчетно-экспериментальных методик оценки показателей надежности. Пример практического применения методики, а также развернутые библиографические данные приведены в приложении 4.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1. ОЦЕНКА НЕСУЩЕЙ СПОСОБНОСТИ ТРУБОПРОВОДОВ, ПРОКЛАДЫВАЕМЫХ В ПРОМЕРЗАЮЩИХ ПУЧИНИСТЫХ ГРУНТАХ
П. 1.1. Предельные состояния трубопроводов при контактном взаимодействии с промерзающим грунтом
Основное требование к трубопроводам как транспортным системам повышенной ответственности с точки зрения обеспечения безопасности состоит в сохранении герметичности и конструкционной целостности в течение всего срока службы. Согласно ГОСТ 27.002-89 "Надежность в технике. Основные понятия. Термины и определения" отказы, последствия которых могут создать угрозу жизни и здоровью людей, либо привести к опасным для человека изменениям в окружающей среде, классифицируются как критические и (или) катастрофические отказы.
Критические отказы участка ЛЧМГ обусловлены, как правило, локальными или протяженными разрушениями трубопровода.
Нарушение герметичности оболочки трубопровода означает безусловное наступление предельного состояния, т.е. такого состояния, при котором дальнейшая эксплуатация трубопровода невозможна по соображениям безопасности и (или) неприемлемых экономических затрат на продолжение эксплуатации.
В то же время для потенциально опасных сооружений и конструкций, к которым принадлежат газо- и нефтепроводы, к категории предельных могут быть отнесены пограничные состояния, реализация которых приводит к существенному повышению риска возникновения критических и (или) катастрофических отказов. К таким состояниям могут быть отнесены предельные состояния, сформулированные в традиционном для строительной механики смысле.
Выделим три типа предельных состояний. Предельное состояние первого типа свяжем с наступлением текучести на некотором участке наиболее нагруженного сечения. В пределе при увеличении внешней нагрузки в этом сечении возможно образование пластического шарнира. Размер пластической зоны будем характеризовать величиной центрального угла y . В качестве наиболее жесткого критерия наступления предельного состояния первого типа примем появление текучести хотя бы в одной точке поперечного сечения. Аналогичное условие часто используют при проведении расчетов на прочность различных строительных конструкций. Если появление пластических деформаций в ограниченной зоне не препятствует нормальной эксплуатации конструкции, то условие может быть ослаблено и допустимый размер пластической зоны увеличен. Критерий может быть записан в виде условия, ограничивающего максимальный уровень отдельных компонент и/или интенсивностей деформаций в характерных точках сечения.
Второй тип предельного состояния свяжем с возникновением местной потери устойчивости в сжатой зоне наиболее нагруженного поперечного сечения. В результате потери устойчивости происходит резкое снижение несущей способности трубопровода по отношению к основным силовым технологическим и природным воздействиям. Локальное снижение жесткости конструкции приводит к изменению силовой схемы по сравнению с первоначальной и, как следствие, изменению реакции на действие приложенных нагрузок. В результате этого происходит прогрессирующее необратимое развитие повреждений и дальнейшее снижение несущей способности.
При третьем типе предельного состояния в трубопроводе в результате контактного взаимодействия с грунтом происходит деформирование и смятие оболочки трубопровода.
Общий признак, характерный для рассматриваемых вариантов предельных состояний, состоит в том, что в отдельных элементах или зонах конструкции появляются большие пластические деформации. В первом случае такая зона возникает в наиболее нагруженной части поперечного сечения, примыкающей к верхней или нижней образующим. Во втором случае она сосредоточена в области гофро-образования, которая появляется в результате местной потери устойчивости. В третьем случае расположение и размеры зоны определяются характером контактного взаимодействия трубопровода с бугром пучинистого грунта, размерами и профилем бугра, масштабами неоднородности пучения вдоль трассы трубопровода.
Наступление предельных состояний данного типа не приводит к непосредственному нарушению герметичности конструкции и тем самым к наступлению критического отказа. Но при этом создаются предпосылки для возникновения критических отказов вследствие реализации непроектных режимов функционирования трубопровода.
Вообще говоря, критерий наступления предельного состояния при контактном взаимодействии с грунтом может быть сформулирован в виде, аналогичном тому, что был использован для предельного состояния первого типа, т.е. в виде ограничений на предельно допускаемые напряжения или деформации. Такое же замечание справедливо по отношению критерия предельного состояния второго типа, связываемого с появлением местной потери устойчивости. Целью разведения критериально схожих предельных состояний по разным типам является желание подчеркнуть уже на уровне формирования критериев предельных состояний характерных особенностей каждого из выделенных типов. Указанные особенности проявляются прежде всего на уровне формирования расчетных схем и моделей, в перечне и форме представления действующих на трубопровод нагрузок и воздействий. В данном случае в качестве критерия наступления предельного состояния третьего типа принято условие, нормирующее предельно допустимый уровень контактной нагрузки на трубопровод со стороны грунта. Предельное значение контактной нагрузки должно быть определено с учетом принятых ограничений на предельно допустимые напряжения и деформации, введенные по критериям предельных состояний первого и второго типов.
Предельные состояния первого и второго типа приближенно могут быть объединены в один расчетный блок и рассмотрены в рамках одной расчетной схемы. При определенном сочетании условий нагружения, физико-механических свойств материала и геометрических размеров трубопровода указанные предельные состояния могут быть реализованы последовательно, причем очередность реализации определяется перечисленной выше совокупностью факторов.
В качестве дополнения к сказанному выше отметим нижеследующее. В зависимости от условий эксплуатации и характерных конструктивных особенностей трубопровода возможно разрушение оболочки трубопровода по механизму отрыва при отсутствии выраженных пластических деформаций, несмотря на высокую начальную пластичность применяемых конструкционных материалов. Охрупчиваемость пластичных материалов проявляется, в частности, в условиях низких эксплуатационных температур и при наличии высокой концентрации напряжений вблизи дефектов. В последнем случае вблизи дефекта происходит искажение номинального напряженно-деформированного состояния конструкции. В условиях стеснения деформаций проявляет себя эффект перенапряжения, приводящий к разрушению конструкции по механизму отрыва при малых незначительных уровнях пластических деформаций. Критерий хрупкой прочности можно рассматривать в качестве альтернативного критерия, основанного на нормировании уровня допустимых деформаций. При наличии концентраторов расчетом должны быть проверены критерии обоих типов и в качестве базовых выбраны те критерии, которые лимитируют прочность конструкции.
П. 1.2. Взаимодействие трубопровода с единичным бугром пучинистого грунта
Ниже представлена расчетная модель, предназначенная для оценки несущей способности трубопровода при взаимодействии с единичным бугром пучинистого грунта. В качестве примера приведены результаты расчета и построения допустимых областей размеров бугров пучения по критериям первого и третьего предельных состояний.
Расчетная модель основана на представлении трубопровода при изгибе упругим стержнем вне зоны контакта и оценке контактного смятия по схеме жестко-пластической оболочки при конечных перемещениях. Схема нагружения трубопровода показана на рис. П. 1.1. Реальный бугор аппроксимирован расчетным бугром прямоугольной формы высотой Н и длиной 2 l 0 . Трубопровод в пределах бугра пучения находится в условиях жесткого кинематического нагружения с заданными перемещениями, равными высоте бугра Н. Вне бугра на трубопровод действует реактивная нагрузка от расположенного выше грунта интенсивностью q . Продольные перемещения трубопровода ограничены силами продольного трения в грунте интенсивностью q ¥ . Параметры q и q ¥ представляют собой статические эквиваленты реальных нагрузок, действующих на отрезок трубопровода длиной в один метр и равны предельным значениям сопротивления грунта вертикальным перемещениям трубопровода и выдергиванию его из грунта. Перемещения трубопровода при изгибе w и параметры l и l ¥ найдем из решения системы уравнений, включающей в общем случае уравнение изгиба стержня, дополненное граничными условиями в сечениях х = l 0 и х = l + l 0 , условие совместности деформаций и уравнение, реализующее условие минимума поперечной силы Q ( l ½ x ) в сечении х = l 0 по параметру l .
Аппроксимируем реальную диаграмму s = s ( e ) расчетной, построенной в предположении, что материал трубопровода идеальный упруго-пластический.
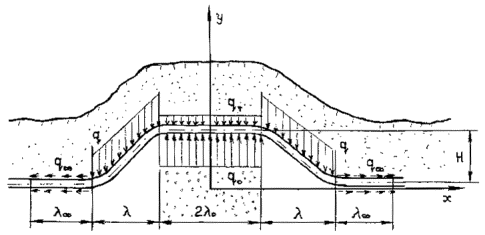
Рис. П. 1.1.Расчетная схема трубопровода при взаимодействии с единичным бугром пучения
Построим зависимость угла y ( c ½ N 0 ), характеризующего размер пластической зоны, от кривизны продольной оси к при заданном значении N 0 . По заданному критическому значению угла y = y а определим значение кривизны c а , при которой y ( c а ½ N 0 ) = y а . Значению а поставим в соответствие изгибающий момент Ма = M ( c а ½ N 0 ), который примем в качестве максимально допустимого по критерию первого предельного состояния. При использовании упругой схемы расчета действительный размер пластической зоны y будет заведомо ниже прогнозируемого, а погрешность расчета пойдет в запас прочности. Аналогичный подход применим при оценке несущей способности по критерию второго предельного состояния / 2/.
Полагаем, что контактное смятие оболочки происходит в условиях стесненного деформирования. При малой глубине смятия Wcr можем пренебречь наличием переходных зон, расположенных слева и справа от бугра и подверженных частичному смятию. Смятие оболочки на центральном участке рассмотрим по схеме цилиндрического изгиба, не учитывая влияния моментов М11, M 12 и усилия N 12 . Полагаем, что участок поперечного сечения, расположенный вне зоны смятия, деформируется упруго. В зоне, подверженной смятию, выполняется условие текучести для цилиндрической оболочки с учетом введенных выше предположений. Предельное контактное усилие qcr ( Wcr ) определим, используя принцип виртуальной мощности / 1/ и откорректировав методологию с учетом действия внутреннего давления р. В качестве критерия предельного состояния третьего типа примем условие q 0 ( H , l 0 ) = qcr ( M 22 , p ½ wcr ), т.е. равенство контактного усилия q 0 ( H , l 0 ) , полученного расчетным путем, предельному qcr ( M 22 , p ½ wcr ) .
П. 1.3. Построение областей предельно допустимых размеров бугров пучения
На рис. П. 1.2 и П. 1.3 показаны области допустимых состояний, построенные на плоскости размеров бугров пучения {2, l 0 , h }. В качестве объекта расчета выбран трубопровод диаметром D =1420 мм и толщиной стенки h =20 мм. Сопротивление грунта продольным перемещениям принято q ¥ =106 Н/м. Графики на рис. П. 1.2 соответствуют предельному сопротивлению грунта вертикальным перемещениям трубопровода q = 5 × 104 Н/м при р=0 ( рис. П. 1.2, а) и р=7,5 МПа ( рис. П. 1.2, б), а на рис. П. 1.3 - аналогичные зависимости при q = 105 Н/м. Трубопровод, загруженный внутренним давлением практически не подвержен смятию при выбранных значениях параметров предельного сопротивления грунта, а его несущая способность определяется сопротивлением конструкции по первому предельному состоянию.
Предположение об абсолютной жесткости бугров морозного пучения во всем диапазоне приложенных нагрузок неизбежно приводит к занижению размеров допускаемой области, особенно в интервале коротких бугров. Очевидно, что под действием приложенной нагрузки некоторое количество бугров будет смято, и не будет представлять опасности для трубопровода. Помимо смятия бугра под нагрузкой отметим еще один фактор, неучет которого приводит к искажению допустимой области. Многочисленными наблюдениями установлено, что под действием внешнего контактного нагружения процесс морозного пучения может быть замедлен и даже прекращен полностью в силу изменения условий промерзания грунта. К таким условиям, например, может быть отнесено изменение структуры грунта, его пористости при уплотнении под нагрузкой, изменение влажности, ограничение под давлением миграции влаги в зону промерзания. Учет указанных факторов даже на основе простейших моделей позволит исключить заведомо нереализуемые на практике варианты.
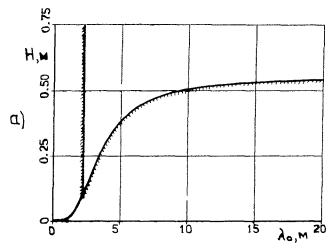
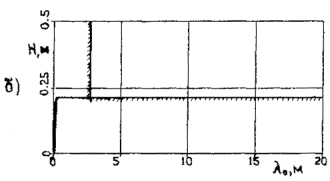
Рис. П. 1.2. Области допустимых состояний при q =5 × 104 Н/м:
а - внутреннее давление р=0; б - р=7,5МПа.
Введем параметр s см - удельную
нагрузку на поверхность бугра, при которой становится невозможным подрастание
бугра пучения или происходит его смятие. С учетом принятой модели контактного
деформирования трубопровода и величины критического смятия w , приближенно оценим площадь Fs поперечного сечения бугра пучения, нагружаемого при
деформировании, и предельную суммарную контактную нагрузку, воспринимаемую
бугром пучения и оболочкой трубопровода без смятия, Q см = s см F см и Pcr = qcr l . Суммарное контактное усилие Q ,
передаваемое на бугор со стороны трубопровода, и предельное сопротивление
трубопровода контактному смятию Pcr
зависят от высоты бугра Н. При Н=0 сопротивление трубопровода смятию имеет
максимальное значение Р ![]() , а при Н=Н m ах - минимальное Р
, а при Н=Н m ах - минимальное Р ![]() . Здесь Hmax -
максимально допустимая высота бугра пучения, определенная по критерию первого
предельного состояния. Характер поправок зависит от соотношения между
параметрами Pcr и Q см в
интервале допустимых значений высот бугров пучения. Если для всех Н из
интервала 0 £ Н £ Н m ах справедливо условие Q см < P с r , -
контактного смятия оболочки не будет. Зная Q ( Hmax ) - суммарную контактную нагрузку на бугор пучения со
стороны трубопровода при Н=Н m ах , определим длину бугра пучения l
. Здесь Hmax -
максимально допустимая высота бугра пучения, определенная по критерию первого
предельного состояния. Характер поправок зависит от соотношения между
параметрами Pcr и Q см в
интервале допустимых значений высот бугров пучения. Если для всех Н из
интервала 0 £ Н £ Н m ах справедливо условие Q см < P с r , -
контактного смятия оболочки не будет. Зная Q ( Hmax ) - суммарную контактную нагрузку на бугор пучения со
стороны трубопровода при Н=Н m ах , определим длину бугра пучения l ![]() , при которой выполняется условие Q ( Hmax ) = s см F см ( l
, при которой выполняется условие Q ( Hmax ) = s см F см ( l ![]() ). При l < l
). При l < l ![]() бугор будет смят до наступления в трубопроводе предельного
состояния первого типа. Допустимая область в этом случае должна быть расширена
за счет подобласти, расположенной левее границы l = l
бугор будет смят до наступления в трубопроводе предельного
состояния первого типа. Допустимая область в этом случае должна быть расширена
за счет подобласти, расположенной левее границы l = l ![]() . Если выполнено условие Qc м > Р
. Если выполнено условие Qc м > Р ![]() , то по отношению к данной конкретной оболочке бугор при
расчете можно считать абсолютно жестким. Выполнение условия Р
, то по отношению к данной конкретной оболочке бугор при
расчете можно считать абсолютно жестким. Выполнение условия Р ![]() < Qc м <Р
< Qc м <Р ![]() означает, что при длине бугра пучения l < l
означает, что при длине бугра пучения l < l ![]() - контактного смятия оболочки не будет. Здесь l
- контактного смятия оболочки не будет. Здесь l ![]() - длина бугра пучения высотой Н
- длина бугра пучения высотой Н ![]() , для которого справедливо условие Q ( l
, для которого справедливо условие Q ( l ![]() )= Pcr (Н
)= Pcr (Н ![]() ½ l
½ l ![]() ). Допустимая область размеров бугров пучения должна быть
расширена за счет включения в нее подобласти, расположенной левее границы l = l
). Допустимая область размеров бугров пучения должна быть
расширена за счет включения в нее подобласти, расположенной левее границы l = l ![]() .
.
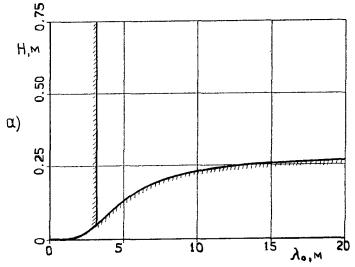
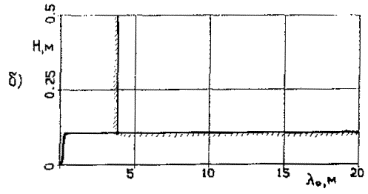
Рис. П.1.3. Области допустимых состояний при q=105Н/м:
а - внутреннее давление р=0; б - р=7,5 МПа.
Границы области допустимых размеров бугров пучения, представленные на рис. П. 1.2 и П. 1.3 и откоректированные с учетом сминаемости мерзлого грунта, отмечены штриховкой с внутренней стороны. Зависимости построены при значении s см =0,5 МПа.
Список использованных источников
1. Ерхов М.И. Теория идеально пластических тел и конструкций. М.: Наука. 1978. 352 с.
2. Вольмир А.С. Устойчивость деформируемых систем. М.: Наука. 1967. 596 с.
ПРИЛОЖЕНИЕ 2. ФОРМИРОВАНИЕ ПРОСТРАНСТВА СОСТОЯНИЙ РАСЧЕТНОГО УЧАСТКА
Решение задачи об определении риска в случае допускаемой области с переменными границами было получено на основе метода, предложенного в / 1/. Предположим, что поведение трубопровода может быть с достаточной полнотой описано при помощи r параметров sn ( n = 1,..., r ), среди которых могут быть как детерминистические, так и случайные величины. Метод предполагает проведение расчетов при различных фиксированных сочетаниях значений параметров s 1 , определение условной безопасности по отношению к каждому фиксированному состоянию трубопровода, последовательный перебор возможных состояний и определение суммарного риска (надежности).
Признаком, идентифицирующим каждое конкретное состояние системы, будем считать детерминистическую совокупность конкретных значений параметров sn (n=1,..., r ), характеризующих свойства, тип и способ взаимодействия конструкции трубопровода с окружающей средой, режимы эксплуатации. Каждому рассматриваемому состоянию присвоим номер a ( a =1,..., m ), который далее будем называть классом состояния. Параметр m равен общему числу возможных состояний. В общем случае, при наличие среди параметров sn ( n =1,..., r ) параметров, имеющих непрерывное распределение в пределах некоторого конечного и неограниченного интервала, число возможных состояний трубопровода будет бесконечно велико. Ограничимся рассмотрением только случая конечного числа возможных состояний. Такой переход возможен, если непрерывно распределенные параметры sn заменить их дискретной аппроксимацией. Механизм перехода будет рассмотрен ниже.
Пусть общее число возможных состояний равно m. Поток элементарных событий (например, возникновение вдоль трассы трубопровода единичного бугра пучения), реализуемый на фоне состояний класса a , образует множество элементарных событий Ф a . Парциальная вероятность Н a представляет собой вероятность того, что среди множества возможных состояний трубопровода на практике будет реализовано состояние, принадлежащее классу a . Сформированное пространство состояний системы должно удовлетворять требованию полноты
![]() ,
(П. 2.1)
,
(П. 2.1)
которое означает, что с вероятностью равной единице трубопровод будет находиться в одном из m рассмотренных состояний, входящих в общее пространство состояний системы.
Если значения параметров sn ( n =1,..., r ) заданы совместной плотностью распределения вероятности p ( s 1 ,..., Sr ), то вероятности Н a ( a =1,..., m ) могут быть получены в результате интегрирования
![]() , (П. 2.2)
, (П. 2.2)
![]()
по r -мерной области W a ( s 1 ,..., sr ), выделяющей в области W ( s 1 ,..., sr ) возможных значений параметров sr подобласть, соответствующую возможным значениям параметров при реализации состояния класса Ф a . Задание подобластей W a возможно различными способами, например при помощи неравенств:
![]() , (П. 2.3)
, (П. 2.3)
где ![]() ,
, ![]() соответствуют
границам интервала возможных значений параметра sn. В качестве
расчетных значений sn при построении области допустимых значений W a можно взять либо среднее из представленного интервала,
либо одно из граничных значений, соответствующее наиболее неблагоприятным
условиям работы трубопровода.
соответствуют
границам интервала возможных значений параметра sn. В качестве
расчетных значений sn при построении области допустимых значений W a можно взять либо среднее из представленного интервала,
либо одно из граничных значений, соответствующее наиболее неблагоприятным
условиям работы трубопровода.
При большом числе определяющих параметров построение совместной плотности распределения p ( s 1,..., sr ) затруднительно. Довольно часто используют предположение о независимости определяющих параметров. Если среди параметров есть заведомо зависящие от некоторых других параметров, то область возможных значений разбивают на подобласти, в каждой из которых параметры можно приближенно считать независимыми, с соответствующей коррекцией плотности распределения вероятности для зависимых параметров.
Для определения парциальных вероятностей Н a необходимо знать вероятности Pkn осуществления каждого из К n возможных значений параметров sn ( n =1,..., r ). Индекс k ( k =1,..., Kn ) соответствует числу интервалов разбиения области возможных значений параметра s n . Для независимого параметра s n вероятность Pnk , может быть определена по известной плотности распределения вероятности pn ( sn ) параметра s n . В этом случае вероятность появления при эксплуатации трубопровода значения параметра s n , принадлежащего интервалу [ snk -1 , snk ], определим по формуле
Pnk 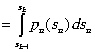 .
(П. 2.4)
.
(П. 2.4)
Значение s 10 соответствует
левой, a s ![]() - правой границе области
возможных значений параметра s 1 . Очевидно, что вероятности Pnk удовлетворяют соотношению
- правой границе области
возможных значений параметра s 1 . Очевидно, что вероятности Pnk удовлетворяют соотношению
![]() .
(П. 2.5)
.
(П. 2.5)
Если среди параметров s 1 есть зависимые, то в этом случае плотность распределения вероятности зависимого параметра должна быть записана как условная плотность вероятности при некоторых фиксированных значениях независимых параметров, являющихся аргументами зависимого параметра. Вычисление вероятностей Р nk проводят требуемое число раз до полного перебора всех возможных комбинаций значений независимых параметров, влияющих на величину зависимого параметра.
Разобьем все параметры на группы по степени взаимного влияния. К элементам первой группы отнесем независимые параметры. Во вторую группу поместим параметры, зависящие только от одного или нескольких параметров первой группы. В третью - параметры, зависящие от элементов первой и второй групп, или только второй групп. И так далее до полного исчерпания списка параметров. Внутри каждой группы считаем параметры (или их наборы) независимыми. Влиянием обратной связи между параметрами пренебрежем. В пределах группы множество возможных значений произвольного зависимого параметра s 1 представим в виде объединения М n независимых подгрупп, каждая из которых содержит К n элементов. Параметр М n , равен числу возможных комбинаций параметров, влияющих на величину параметра sn . В результате, любое из возможных состояний трубопровода можем представить в виде последовательного соединения элементов, принадлежащих различным группам, по одному из каждого вертикального слоя, соответствующего множеству возможных значений параметра sn ( n =1,..., r ). Пример такого представления дан на рис. П. 2.1. Верхний индекс у зависимых элементов обозначает номер подгруппы в группе или, что одно и то же, номер комбинации независимых параметров, влияющих на величину данного параметра. Вероятность Н a равна произведению вероятностей элементов, образующих соответствующее последовательное соединение.
На рис. П. 2.2 изображена схема, поясняющая изложенные рассуждения в случае описания поведения трубопровода четырьмя характеристическими параметрами. Список параметров составлен в соответствии с требованиями методики расчета взаимодействия трубопровода с единичным бугром пучинистого грунта по схеме, приведенной в Приложении : s 1 = p - внутреннее давление, s 2 =Т - температура стенок оболочки трубопровода, s 3 = q - интенсивность силового воздействия на трубопровод, s 4 = q ¥ - интенсивность сил продольного трения.
Внутреннее давление р считаем
независимым параметром. Температура стенок в общем случае зависит сложным
образом от температуры окружающего грунта, режима эксплуатации трубопровода,
удаленности рассматриваемого участка ЛЧМГ от компрессорной станции и ряда
других факторов. В данном примере, учитывая его иллюстративный характер, будем
приближенно считать, что температура стенок Т зависит только от режима
эксплуатации трубопровода, т.е. от давления р. Параметры q и q ¥ считаем независимыми между собой, но зависящими от температуры
стенок. Предположим, что возможны только два альтернативных режима
эксплуатации. Первый - это режим нормальной эксплуатации с давлением
перекачиваемого продукта р=7,5 МПа. Второй режим соответствует состоянию
простоя и р=0.0. Вероятность осуществления первого режима Р11=0,95,
второго - P 12 =0,05 за
рассматриваемый период. Предположим, что с вероятностью равной единице при
нормальном режиме эксплуатации температура стенок будет равна Т ![]() = -2 °С, а в простаивающем трубопроводе Т
= -2 °С, а в простаивающем трубопроводе Т ![]() = -10 °С. Верхний индекс обозначает номер комбинации
независимых параметров, влияющих на величину параметра s 2 =Т. В данном случае
таких комбинаций (поскольку независимый параметр один, речь идет не о
комбинации, а о числе возможных значений независимого параметра) М2=2.
В такой постановке можем считать параметр s 2 детерминистическим
при условии, что задана величина внутреннего давления. Следовательно, множество
возможных состояний трубопровода можно представить графически в виде двух независимых
подмножеств. В пределах каждого из подмножеств вычисление вероятностей Pnk проводим без учета состояний, отнесенных к другим
подмножествам. Условие (П.
2.5) справедливо только по отношению к вероятностям состояний,
принадлежащих одному и тому же подмножеству. Множество возможных значений
параметров q и q „ o
разбиваем на четыре интервала. Результаты вычислений представлены в табл. П. 2.1.
= -10 °С. Верхний индекс обозначает номер комбинации
независимых параметров, влияющих на величину параметра s 2 =Т. В данном случае
таких комбинаций (поскольку независимый параметр один, речь идет не о
комбинации, а о числе возможных значений независимого параметра) М2=2.
В такой постановке можем считать параметр s 2 детерминистическим
при условии, что задана величина внутреннего давления. Следовательно, множество
возможных состояний трубопровода можно представить графически в виде двух независимых
подмножеств. В пределах каждого из подмножеств вычисление вероятностей Pnk проводим без учета состояний, отнесенных к другим
подмножествам. Условие (П.
2.5) справедливо только по отношению к вероятностям состояний,
принадлежащих одному и тому же подмножеству. Множество возможных значений
параметров q и q „ o
разбиваем на четыре интервала. Результаты вычислений представлены в табл. П. 2.1.
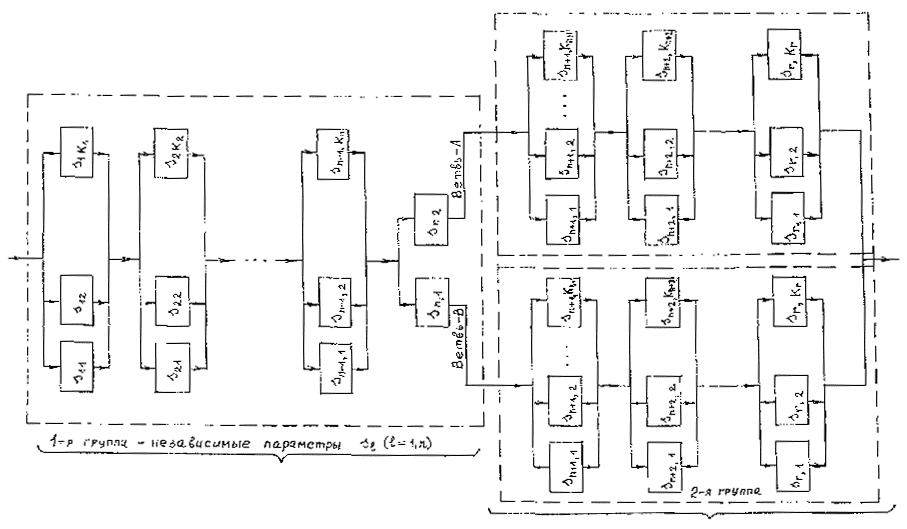
Рис. П. 2.1. Представление текущего состояния трубопровода в виде последовательного соединения элементов, принадлежащих различным группам
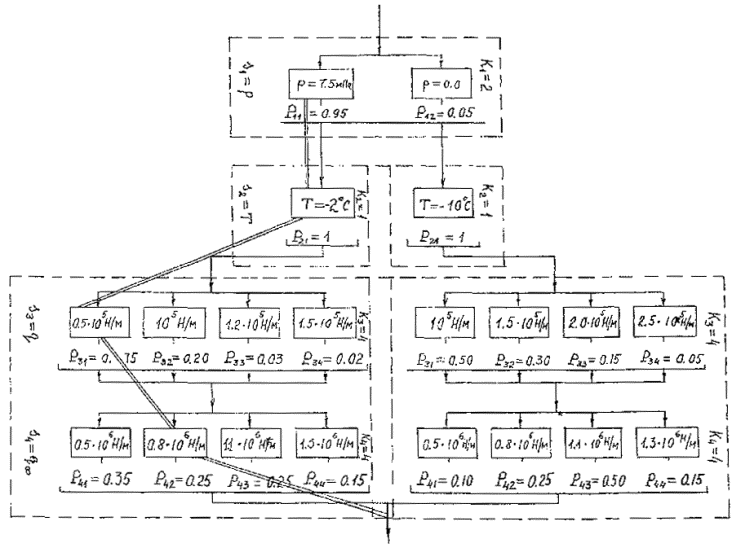
Рис. П. 2.2. Схема вычисления парциальной вероятности Н a
Таблица П. 2.1.
|
Температура Т,°С |
Интенсивность внешней нагрузки q , H / M |
Интенсивность сил продольного трения q ¥ , Н/м |
Вероятности |
|
|
P 3 k |
P 4 k |
|||
|
-2 |
0,5 ´ 105 |
- |
0,75 |
- |
|
1,0 ´ 105 |
0,20 |
|||
|
1,2 ´ 105 |
0,03 |
|||
|
1,5 ´ 105 |
0,02 |
|||
|
-10 |
1,0 ´ 105 |
- |
0,50 |
- |
|
1,5 ´ 105 |
0,30 |
|||
|
2,0 ´ 105 |
0,15 |
|||
|
2,5 ´ 105 |
0,05 |
|||
|
-2 |
- |
0,5 ´ 106 |
- |
0,35 |
|
0,8 ´ 106 |
0,25 |
|||
|
1,1 ´ 106 |
0,25 |
|||
|
1,3 ´ 106 |
0,15 |
|||
|
-10 |
- |
0,5 ´ 106 |
- |
0,10 |
|
0,8 ´ 106 |
0,25 |
|||
|
1,1 ´ 106 |
0,50 |
|||
|
1,3 ´ 106 |
0,15 |
|||
В
представленном примере общее число возможных состояний m
= 32. Вероятность осуществления состояния с параметрами, например, р = 7,5 МПа,
Т = -2 °С, q = 5 × 104 Н/м и q ¥ = 0,8 × 106 Н/м, определим простым перемножением
вероятностей: Н a =Р11 × р ![]() р
р ![]() p
p ![]() =0,178125.
=0,178125.
Очевидно, что чем полнее представлено пространство возможных состояний (чем разветвленное "дерево состояний"), тем достовернее будут получаемые оценки показателей надежности. Ограничениями являются только рост расчетного времени и дополнительные трудности в сборе необходимых статистических данных о вероятностях Pnk .
Список использованных источников
1. Болотин В.В. Прогнозирование ресурса машин и конструкций. М.: Машиностроение. 1984. 312с.
ПРИЛОЖЕНИЕ 3. ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ЛИНЕЙНЫХ ЧАСТЕЙ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ, ПРОКЛАДЫВАЕМЫХ В ПРОМЕРЗАЮЩИХ ПУЧИНИСТЫХ ГРУНТАХ
П. 3.1. Постановка задачи об оценке показателей надежности протяженных конструкций
Линейные части трубопроводов представляют собой протяженные конструкции, эксплуатируемые в течение заданного срока. Неоднородность нагрузок и воздействий на различных участках трубопровода является причиной различий в уровне надежности составляющих его элементов. Поэтому в общем случае при оценке показателей надежности необходимо учитывать развертывание нагрузок и свойств трубопровода во времени. Отказ в этом случае будет связан с выбросом за пределы допустимой области W значений некоторой случайной функции w ( x , t ), описывающей поведение трубопровода и зависящей от двух независимых координат - осевой координаты и времени. Надежность трубопровода R ( t ) по отношению к рассмотренным выше типам предельных состояний определим через вероятность P { w ( t ) Î W ½ t Î [0, t ] того, что на участке трубопровода заданной длины L не произойдет ни одного случая наступления предельного состояния за весь плановый срок эксплуатации t . Дополнение вероятности безотказной работы до единицы Q ( t ) назовем риском возникновения предельного состояния.
Оценку риска, связанного с возникновением предельного состояния в трубопроводе, проведем на основе метода, предложенного В.В. Болотиным / 1/. В качестве элементарного события будем рассматривать возникновение единичного бугра вдоль трассы трубопровода. Бугры пучения, расположенные последовательно вдоль трассы трубопровода, образуют поток элементарных событий на координатной оси Ох. Наступление предельного состояния свяжем с выходом размеров бугров пучения за пределы допустимой области W , определенной на основе детерминистического расчета. Тип, конфигурация и размеры допустимой области зависят от выбора функции качества w ( x , t ) и варианта расчетного метода, используемого для ее построения. В качестве примера на рис. П. 1.2 и П. 1.3 приведены области W a , построенные на плоскости размеров бугров пучения ( l о , Н), при различных значениях q . Очевидно, что приведенные примеры не исчерпывают возможные варианты построения допустимых областей.
Предположим, что последовательность бугров пучения вдоль трассы трубопровода образует пуассоновский поток. В этом случае вероятность возникновения k бугров на участке длиной L можем определить по формуле
Pk = ( m L)k/k! exp(- m L),
где m - математическое ожидание числа бугров на единицу длины трубопровода, которое здесь считаем известным. Размеры бугра пучения l 0 и Н задаются парой случайных чисел с заданной совместной плотностью распределения вероятности р( l 0 , Н). Если за расчетные значения нагрузок и их сочетаний принять нагрузки, соответствующие периоду с наиболее неблагоприятными условиями работы трубопровода продолжительностью t 1 , то для оценки риска в случае пуассоновского потока событий может быть использована следующая формула
Q ![]() (П. 3.1)
(П. 3.1)
Формула (П. 3.1) позволяет получить верхнюю оценку для полного риска Q с учетом многообразия возможных состояний трубопровода в процессе эксплуатации. С этой целью множество возможных состояний трубопровода разбито на m классов. Для каждого из них определена парциальная вероятность H a того, что в процессе функционирования трубопровода возникнет состояние именно a -го класса. Условная безопасность S a имеет смысл вероятности невозникновения предельного состояния при реализации элементарного события, принадлежащего множеству Ф a ( см. Приложение 2).
Трубопровод общей длиной L
разобьем на NL расчетных участка длиной D Li ( L ![]() ). Цель разбиения состоит в
выделении участков с однородными условиями эксплуатации. Общие правила
разбиения на расчетные участки и условия, достаточные для выделения расчетного
участка изложены в основной части данного документа ( раздел 3.5). Для трубопроводов, проложенных в
промерзающих пучинистых грунтах, необходимо дополнительное деление участков по
грунтово-геологическим признакам, в состав которые входят характеристики
морозного пучения. Перечень включаемых характеристик определяется в
соответствии с выбранной расчетной моделью.
). Цель разбиения состоит в
выделении участков с однородными условиями эксплуатации. Общие правила
разбиения на расчетные участки и условия, достаточные для выделения расчетного
участка изложены в основной части данного документа ( раздел 3.5). Для трубопроводов, проложенных в
промерзающих пучинистых грунтах, необходимо дополнительное деление участков по
грунтово-геологическим признакам, в состав которые входят характеристики
морозного пучения. Перечень включаемых характеристик определяется в
соответствии с выбранной расчетной моделью.
Однородность по выбранным параметрам должна быть обеспечена в течение всего временного интервала, на котором прогнозируются соответствующие показатели надежности. В противном случае при изменении условий эксплуатации необходимо производить переформирование расчетных участков.
Сформируем пространство состояний в соответствии с методикой, представленной в Приложении 2, включая определение парциальных вероятностей Н a того, что в процессе функционирования трубопровода возникнет состояние именно a -го класса. После этого, для практического применения формулы (П. 3.1) для расчета вероятности безотказной работы необходимо определить условную безопасность S a . Параметры S a представляют собой вероятности невозникновения предельного состояния при реализации состояния трубопровода, принадлежащего к классу a .
П.3.2. Оценка условной безопасности S a методом статистического моделирования
Применительно к рассматриваемому случаю определение условной безопасности S „ эквивалентно определению вероятности Р {( l 0 , Н) Î W a ½ Ф a }. При известной совместной плотности распределения вероятности размеров бугров пучения р( l 0 , Н ½ Ф a ), условную безопасность S a в общем случае можем вычислить по формуле
S a ![]() (П. 3.2)
(П. 3.2)
( l 0 , Н) Î W a
В зависимости от вида функции р( l 0 , Н ½ Ф a ) интегралы в (П. 3.2) могут быть получены аналитически или в результате численного интегрирования.
В данной работе в основу
определения условной безопасности S a положен метод статистического моделирования. Он состоит в
моделировании размеров бугров пучения и подсчете числа выбросов за пределы
допустимой области W a . При длине смоделированной реализации N a и числе выбросов за пределы допустимой области ![]() a приближенная оценка для условной безопасности
a приближенная оценка для условной безопасности ![]() a может быть получена на основе следующей формулы:
a может быть получена на основе следующей формулы: ![]() . Параметры вероятностного распределения устанавливаются в
зависимости от класса состояния трубопровода. Для учета статистического
разброса значений параметров вероятностных распределений, в общем случае,
целесообразно включить такие параметры, как математическое ожидание, дисперсия
и другие в перечень определяющих параметров, аналогично параметрам s 1 ,... sr . При этом обратим внимание на существенное отличие
параметров распределений от параметров s 1 ,... sr . В отличие от последних, параметры вероятностных
распределений не влияют на размеры и конфигурацию допустимой области W a . Влияние этих параметров проявляется на следующем этапе -
при оценке значения S a . Поэтому учет разброса
параметров вероятностных распределений, их зависимость от условий эксплуатации
трубопровода целесообразно проводить именно на этом этапе. Механизм учета
аналогичен изложенному в
Приложении 2. Для каждого состояния класса a ( a = 1,..., m )
сформируем набор, состоящий из n a комбинаций параметров распределения. Для каждой комбинации
оценим вероятность w a g ( g = 1,..., n a ) осуществления данной совокупности значений параметров,
при условии что реализовано состояние класса a . Затем производим последовательное моделирование и оценку
условной безопасности
. Параметры вероятностного распределения устанавливаются в
зависимости от класса состояния трубопровода. Для учета статистического
разброса значений параметров вероятностных распределений, в общем случае,
целесообразно включить такие параметры, как математическое ожидание, дисперсия
и другие в перечень определяющих параметров, аналогично параметрам s 1 ,... sr . При этом обратим внимание на существенное отличие
параметров распределений от параметров s 1 ,... sr . В отличие от последних, параметры вероятностных
распределений не влияют на размеры и конфигурацию допустимой области W a . Влияние этих параметров проявляется на следующем этапе -
при оценке значения S a . Поэтому учет разброса
параметров вероятностных распределений, их зависимость от условий эксплуатации
трубопровода целесообразно проводить именно на этом этапе. Механизм учета
аналогичен изложенному в
Приложении 2. Для каждого состояния класса a ( a = 1,..., m )
сформируем набор, состоящий из n a комбинаций параметров распределения. Для каждой комбинации
оценим вероятность w a g ( g = 1,..., n a ) осуществления данной совокупности значений параметров,
при условии что реализовано состояние класса a . Затем производим последовательное моделирование и оценку
условной безопасности ![]() a g , при сформированных комбинациях значений параметров
вероятностных распределений. Значение условной безопасности
a g , при сформированных комбинациях значений параметров
вероятностных распределений. Значение условной безопасности ![]() a , учитывающее разброс значений параметров статистических
распределений, получим как
a , учитывающее разброс значений параметров статистических
распределений, получим как
![]() ( a =1,..., m )
( a =1,..., m )
Моделирование случайных последовательностей с заданным типом распределения основано на использовании метода обратных функций. Если вероятностное распределение таково, что построение обратной функции затруднительно, то для моделирования применим метод Неймана / 3/.
В данной работе реализованы
различные подходы к моделированию размеров бугров пучения. Наиболее простой
основан на предположении о взаимной статистической независимости указанных
величин, каждая из которых подчиняется заданному типу распределения. В общем
случае такое предположение вступает в некоторое противоречие с данными натурных
наблюдений. Корреляция между длиной и высотой бугра наиболее ярко выражена в
области малых длин бугров 0< l 0 < l a . В этом интервале взаимная корреляция может быть учтена
введением вспомогательной случайной величины u =Н/ l 0 . Если известны
математические ожидания < l >
и <Н> и дисперсии s ![]()
![]() и s
и s ![]() размеров бугров, то аналогичные статистические
характеристики случайной величины и определим по формулам
размеров бугров, то аналогичные статистические
характеристики случайной величины и определим по формулам
<u>=<H>/< l 0 >, ![]() .
( П . 3.3)
.
( П . 3.3)
Условие (П. 3.3) накладывает ограничения на возможные значения статистических характеристик l 0 и Н: s Н /<Н> s l /< l 0 >. Численное значение параметра l а зависит от целого ряда факторов и его выбор, вообще говоря, не может быть жестко регламентирован. При l 0 > l а статистическая связь между длиной и высотой бугра ослабевает. При больших значениях < l 0 > статистической связью между размерами l 0 и Н можно пренебречь.
В качестве базовых при моделировании размеров бугров пучения использованы нормальное распределение и трехпараметрическое распределение Вейбулла
![]() (П.3.4.)
(П.3.4.)
В формуле (П. 3.4) вместо х должны быть подставлены Н и l 0 . В качестве оценок параметров сдвига в распределениях примем d Н = 0 и d l = l 0 min . Значение l 0 min равно минимальной длине бугра, фиксируемой при наблюдениях. Оставшиеся неизвестные параметры распределения Вейбулла q х и a х определим из соотношений, связывающих их с известными оценками математического ожидания и дисперсии
<Х>= d х +( q х - d х )Г(1+1/ a х ) (П.3.5)
Dx = ( q х - d х )2[Г(1+2/ a х ) - Г2(1+1/ a х )]
Корни системы (П. 3.5) d х и a х найдем, используя разложение в ряд гамма-функции Г(1 + b ) /2/ и применяя процедуру итерационного уточнения. Оценки математических ожиданий и дисперсий случайных величин могут быть получены из анализа экспериментальных данных о пучении грунтов / 4/.
Неполнота и недостоверность статистической информации об основных параметрах, характеризующих процесс морозного пучения, ограничивает возможности обоснования однозначного выбора используемых типов вероятностных распределений. Поэтому приведенные в данной работе расчетные примеры не несут нормативного назначения и имеют скорее демонстрационный, модельный характер. Однако они могут быть рекомендованы для исследования основных качественных характеристик рассматриваемых процессов. Использование в данной работе конкретных типов распределений не является жестким ограничением области применения расчетной методики. При необходимости заменой практически только одного программного модуля методика может быть адаптирована к требуемому типу вероятностного распределения.
П.3.3. Обсуждение численных результатов
На рис. П. 3.1 и П. 3.2 приведены результаты моделирования размеров бугров пучения с использованием нормального и вейбулловского распределений. Расчеты проведены при следующих значениях статистических характеристик длин l 0 и высот Н бугров пучения: < l 0 >=10 м, s l =5 м, <Н>=0,1 м, s Н =0,06м. Для наглядности помимо маркеров, показывающих размеры бугров, на плоскости l 0 , Н нанесена граница допускаемой области W , представленной ранее на рис. П. 1.2, а. На рис. П. 3.1,а показаны результаты моделирования, проведенного в предположении, что значения l 0 и Н не коррелируют между собой и подчиняются распределению Вейбулла. На рис. П. 3.1.б - длина l 0 и высота бугра связаны между собой через параметр u . На рис. П. 3.2, а приведены результаты моделирования размеров бугров в предположении, что параметры l 0 и Н независимы и подчиняются нормальному распределению ( рис. П. 3.2, а). На рис. П. 3.2, б размеры бугров также независимы между собой, но длина бугров l 0 подчиняется нормальному, а высота Н - распределению Вейбулла. На рис. П. 3.1 и П. 3.2 не показаны точки, попавшие в область отрицательных значений при использовании нормального распределения. При выбранных значениях математического ожидания и дисперсии общее количество таких точек не превышало нескольких процентов от общей длины реализации.
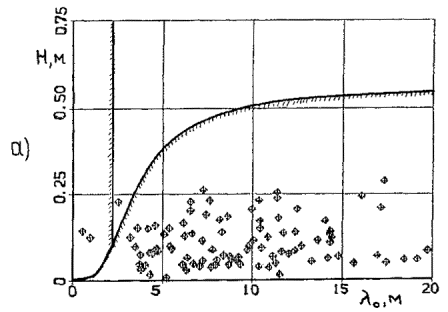
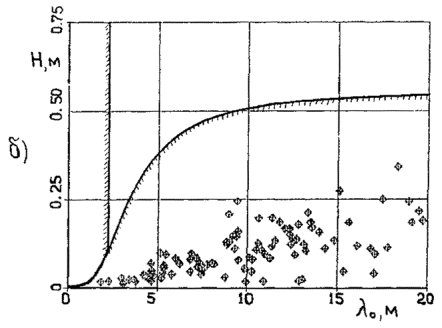
Рис. П. 3.1. Результаты моделирования размеров бугров в случае независимых значений l 0 и Н:
а) связанных через параметр u , б) значения l 0 и Н в первом и l 0 и u во втором случаях подчиняются распределению Вейбулла.
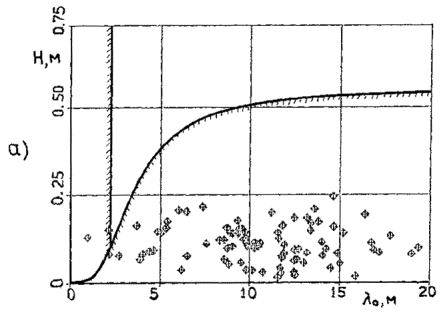
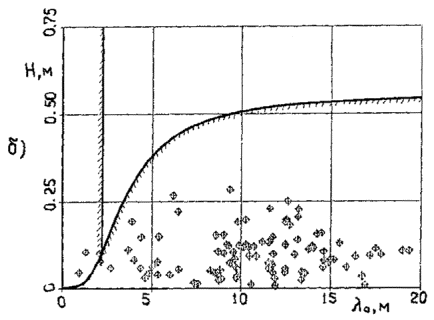
Рис. П. 3.2. Результаты моделирования размеров бугров в случае независимых значений l 0 и Н
а) распределенных по нормальному закону, б) длины бугров l 0 подчиняются нормальному, а высоты Н - распределению Вейбулла
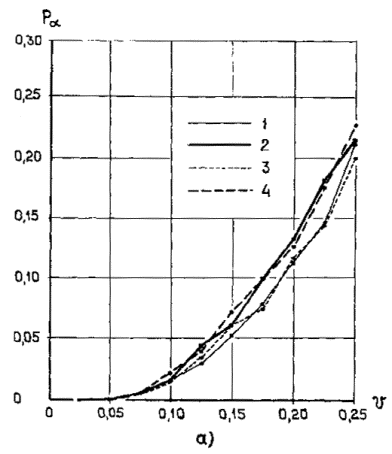
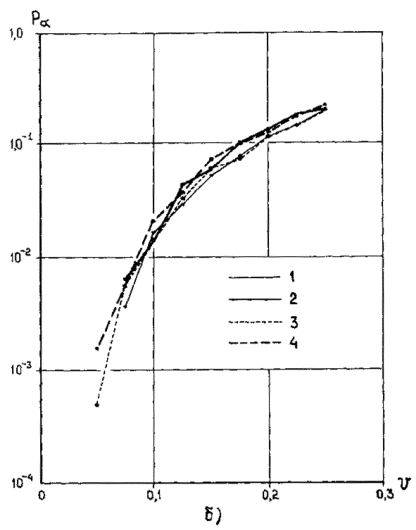
Рис. П. 3.3. Расчетная оценка вероятности R a появления бугра с размерами, выходящими за пределы допускаемой области, как функции <Н> при фиксированных значениях <Н>/ s Н = 0,5, < l 0 > = 5 м и s l = 2,5 м;
а - декартова система координат, б - логарифмическая шкала по оси ординат
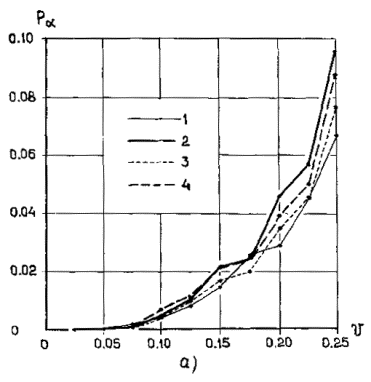
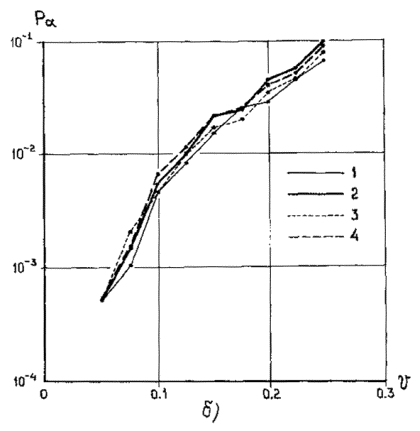
Рис. П. 3.4. Расчетная оценка вероятности R a появления бугра с размерами, выходящими за пределы допускаемой области, как функции <Н> при фиксированных значениях <Н>/ s H = 0,5, < l 0 > = 10 м и s l = 2,5 м;
а - декартова система координат, б - логарифмическая шкала по оси ординат
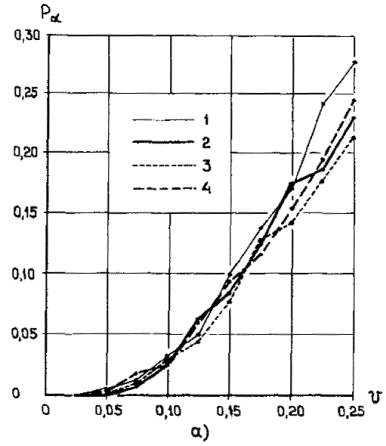
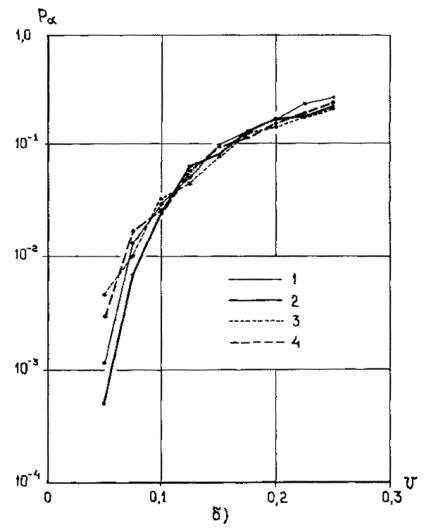
Рис. П. 3.5. Расчетная оценка вероятности R a появления бугра с размерами, выходящими за пределы допускаемой области, как функции <Н> при фиксированных значениях <Н>/ s Н = 0,8, < l 0 > = 5 м и s l =2,5 м; для независимых и взаимно-коррелированных последовательностей l 0 и Н;
а - декартова система координат, б - логарифмическая шкала по оси ординат
На рис. П. 3.3 - П. 3.5 приведены результаты вычисления вероятности R a =1 - S a появления бугров пучения с размерами, выходящими за
пределы допускаемой области. Графики в каждой из групп построены при
фиксированных значениях математического ожидания < l 0 > и дисперсии s ![]() длины бугра пучения как функции отношения v = <Н>/ s H . Зависимости построены для различных типов вероятностных
распределений в предположении о взаимной статистической независимости и
взаимной коррелированности случайных последовательностей l 0 и Н. Графики на рис. П. 3.3 и П. 3.4 построены в предположении, что параметры l 0 и Н не коррелируют
между собой. При моделировании случайных последовательностей использованы
следующие числовые значения: < l 0 > 5 м, s l =2,5м, математическое ожидание высоты бугра <Н>
выбиралось из интервала 0,025 £ <Н> £ 0,25 (м), s H /<Н> = 0,5. Номера маркеров на графике соответствуют
следующим типам распределений: 1 - нормальное распределение для l 0 и Н; 2- распределение Вейбулла для l 0 и Н; 3- нормальное для l 0 , распределение Вейбулла для Н; 4 - распределение Вейбулла
для l 0 и нормальное распределение для Н. Графики на рис. П. 3.3.а построены в
декартовой системе координат, а на
рис. П. 3.3, б - значения R a отложены в логарифмической шкале, что делает график более
наглядным в области малых вероятностей. Аналогичные зависимости для < l 0 > = 10 м и s l = 5м представлены на рис. П. 3.4,а и П. 3.4,б. Графики построены по результатам
осреднения значений вероятностей, полученных по 10 реализациям стандартной
длиной N = 5000 точек каждая. Для используемых типов распределений во всем
диапазоне изменения параметра v = s l /<Н> получены вполне сопоставимые значения
вероятностей выбросов за пределы допустимой области. Наибольшее расхождение
характерно для области малых и относительно больших по сравнению с
соответствующими критическими значениями высот бугров значений <Н>.
Возрастание числа выбросов за пределы допустимой области при уменьшении
величины математического ожидания длины бугра до < l 0 > = 5 м вызвано, с одной стороны, характерной
конфигурацией допустимой области, а с другой - неучетом взаимной корреляции
длин и высот бугров пучения в области малых значений l 0 . На рис. П. 3.5
приведены графики вероятностей выбросов за пределы области при моделировании
несвязанных и взаимно-коррелированных реализации размеров бугров. При этом
использованы следующие числовые значения параметров: < l 0 > = 5 м, s l =2,5 м, 0,025 <Н> 0,25 м, s Н /<Н>=0,8.
Номера маркеров соответствуют следующим типам зависимостей: 1 - независимые
реализации, распределенные по нормальному закону; 2 - независимые реализации l 0 и Н, распределенные по Вейбуллу; 3 - независимые
реализации l 0 и Н, длина бугра распределена по нормальному закону,
высота Н удовлетворяет распределению Вейбулла; 4 - взаимно-коррелированные
реализации l 0 и Н, связанные через параметр и, длина бугра l 0 и параметр u подчиняются
распределению Вейбулла. Увеличение относительной величины дисперсии высоты
бугра по сравнению с примером, представленным на рис. П. 3.3, приводит к общему возрастанию
вероятности выброса для соответствующих зависимостей. При использовании
взаимно-коррелированных последовательностей типа 4 вероятность выбросов в
области малых значений <Н> снижается на порядок и более по сравнению,
например, с аналогичной зависимостью для некоррелированных значений l 0 и
Н (индекс 2).
длины бугра пучения как функции отношения v = <Н>/ s H . Зависимости построены для различных типов вероятностных
распределений в предположении о взаимной статистической независимости и
взаимной коррелированности случайных последовательностей l 0 и Н. Графики на рис. П. 3.3 и П. 3.4 построены в предположении, что параметры l 0 и Н не коррелируют
между собой. При моделировании случайных последовательностей использованы
следующие числовые значения: < l 0 > 5 м, s l =2,5м, математическое ожидание высоты бугра <Н>
выбиралось из интервала 0,025 £ <Н> £ 0,25 (м), s H /<Н> = 0,5. Номера маркеров на графике соответствуют
следующим типам распределений: 1 - нормальное распределение для l 0 и Н; 2- распределение Вейбулла для l 0 и Н; 3- нормальное для l 0 , распределение Вейбулла для Н; 4 - распределение Вейбулла
для l 0 и нормальное распределение для Н. Графики на рис. П. 3.3.а построены в
декартовой системе координат, а на
рис. П. 3.3, б - значения R a отложены в логарифмической шкале, что делает график более
наглядным в области малых вероятностей. Аналогичные зависимости для < l 0 > = 10 м и s l = 5м представлены на рис. П. 3.4,а и П. 3.4,б. Графики построены по результатам
осреднения значений вероятностей, полученных по 10 реализациям стандартной
длиной N = 5000 точек каждая. Для используемых типов распределений во всем
диапазоне изменения параметра v = s l /<Н> получены вполне сопоставимые значения
вероятностей выбросов за пределы допустимой области. Наибольшее расхождение
характерно для области малых и относительно больших по сравнению с
соответствующими критическими значениями высот бугров значений <Н>.
Возрастание числа выбросов за пределы допустимой области при уменьшении
величины математического ожидания длины бугра до < l 0 > = 5 м вызвано, с одной стороны, характерной
конфигурацией допустимой области, а с другой - неучетом взаимной корреляции
длин и высот бугров пучения в области малых значений l 0 . На рис. П. 3.5
приведены графики вероятностей выбросов за пределы области при моделировании
несвязанных и взаимно-коррелированных реализации размеров бугров. При этом
использованы следующие числовые значения параметров: < l 0 > = 5 м, s l =2,5 м, 0,025 <Н> 0,25 м, s Н /<Н>=0,8.
Номера маркеров соответствуют следующим типам зависимостей: 1 - независимые
реализации, распределенные по нормальному закону; 2 - независимые реализации l 0 и Н, распределенные по Вейбуллу; 3 - независимые
реализации l 0 и Н, длина бугра распределена по нормальному закону,
высота Н удовлетворяет распределению Вейбулла; 4 - взаимно-коррелированные
реализации l 0 и Н, связанные через параметр и, длина бугра l 0 и параметр u подчиняются
распределению Вейбулла. Увеличение относительной величины дисперсии высоты
бугра по сравнению с примером, представленным на рис. П. 3.3, приводит к общему возрастанию
вероятности выброса для соответствующих зависимостей. При использовании
взаимно-коррелированных последовательностей типа 4 вероятность выбросов в
области малых значений <Н> снижается на порядок и более по сравнению,
например, с аналогичной зависимостью для некоррелированных значений l 0 и
Н (индекс 2).
Список использованных источников
1. Болотин В.В. Прогнозирование ресурса машин и конструкций. М.: Машиностроение. 1984. 312 с.
2. Двайт Г.Б. Таблицы интегралов и другие математические формулы. М.: Наука. 1977. 224 с.
3. Капур К., Ламберсон Л. Надежность и проектирование систем. М.: Мир. 1980. 604 с.
4. Невечеря В.Л., Горальчук М.И. Некоторые закономерности сезонного пучения грунтов в северотаежной зоне Западной Сибири // Криогенные процессы. М.: Наука. 1978. С. 177-188.
ПРИЛОЖЕНИЕ 4. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ И ДОЛГОВЕЧНОСТИ ПО ОТНОШЕНИЮ К КРИТИЧЕСКИМ ОТКАЗАМ, СВЯЗАННЫМ С РОСТОМ УСТАЛОСТНЫХ ТРЕЩИН, В НАДЗЕМНЫХ ГАЗОПРОВОДАХ ПРИ ДЕЙСТВИИ ВЕТРОВОЙ НАГРУЗКИ И ПРОСАДКЕ ОПОР
Применение методологии предполагает решение следующих частных задач:
- расчет колебательного режима газопровода с учетом ударного взаимодействия с опорой;
- анализ напряженно-деформированного состояния в окрестности трещины, локализованной зоной контакта поверхности трубы с просевшей опорой;
- формирование пространства состояний расчетного участка трубы с трещиной по возможным режимам нагружения трубопровода;
- расчет роста усталостной трещины при заданных режимах нагружения (для каждого класса состояний расчетного участка);
- моделирование псевдослучайной выборки параметров начальных трещин и вычисление выборочных параметров функции распределения экстремальных времен отказов;
- оценка показателей надежности и долговечности расчетного участка по совокупности возможных состояний на прогнозируемый срок эксплуатации.
П.4.1. Формирование расчетных участков
П.4.1.1. За расчетный участок для расчета колебательного режима трубопровода под действием ветровой нагрузки с учетом контактного взаимодействия с просевшей опорой принимается двухпролетная балочная модель трубы с центральной опорой, имеющей зазор D в свободном состоянии. Расчет колебательного режима проводится методами строительной механики с целью получения функций перемещений центральной оси трубопровода в зависимости от времени (числа циклов колебаний в ветровом потоке). Для выполнения расчетов разработан программный комплекс WIND / 1- 3/.
П.4.1.2. За расчетный участок для оценки роста усталостных трещин принимается элемент цилиндрической оболочки на нижней образующей трубы в зоне контакта ее с опорой. Размеры сегмента трубы должны быть не меньше 41, где 1 - длина трещины на нижней образующей. Различаются трещины, ориентированные вдоль образующей (осевые) и поперек (кольцевые). Трещины произвольной ориентации не рассматриваются, т. к. при расчете заменяются эквивалентными, ориентированными в указанных направлениях, как наиболее опасными.
П.4.1.3. При расчете напряженного состояния на расчетных участках второго типа определяются продольные и кольцевые напряжения на границах данных расчетных участков (функции номинальных напряжений в стенке трубы в зависимости от режима колебаний в ветровом потоке и величины зазора Д), которые определяют рост кольцевых и осевых трещин, соответственно. Расчеты напряжений могут быть проведены на основе приложений к программному комплексу WIND / 1- 3/.
П.4.2. Формирование пространства состояний расчетного участка
Приведем конкретный пример формирования пространства состояний расчетного участка с трещиной с учетом четырех режимов нагружения и различных типов дефектов. Полная прогнозируемая наработка - Т * = D Т1 + D Т2 + D Т3 + D Т4, где D Ti - наработки по четырем сезонам однородной ветровой нагрузки, степени контактного взаимодействия с опорой, постоянных нагрузок и т.п. Отдельные наработки имеют значения: D T 1 = 20 суток, D T 2 = 40 суток, D Т3 = 30 суток, D Т4 = 50 суток.
П.4.2.1. Формирование классов по режимам нагружения:
1) сезон 1: наработка изменяется в интервале 0 £ Т £ D T 1 , что соответствует номинальным напряжениям в стенке трубы
s ![]() = 150МПа, s
= 150МПа, s ![]() = 150МПа, постоянные составляющие
= 150МПа, постоянные составляющие
s ![]() = 250 МПа, s
= 250 МПа, s ![]() = 250 МПа,
= 250 МПа,
D s ![]() = 50 МПа, D s
= 50 МПа, D s ![]() = 20 МПа, размахи циклических напряжений
= 20 МПа, размахи циклических напряжений
D s ![]() = 150 МПа, D s
= 150 МПа, D s ![]() = 100 МПа,
= 100 МПа,
2) сезон 2: наработка изменяется в интервале D Т1 £ Т £ D Т1 + D Т2, что соответствует номинальным напряжениям в стенке трубы
s ![]() = 150 МПа, s
= 150 МПа, s ![]() = 100 МПа,
= 100 МПа,
s ![]() = 200 МПа, s
= 200 МПа, s ![]() = 200 МПа,
= 200 МПа,
D s ![]() = 50 МПа, D s
= 50 МПа, D s ![]() = 10 МПа,
= 10 МПа,
D s ![]() = 150 МПа, D s
= 150 МПа, D s ![]() = 50 МПа,
= 50 МПа,
3) сезон 3: наработка изменяется в интервале D Т1 + D Т2 £ Т £ D Т1 + D Т2 + D Т3, что соответствует номинальным напряжениям в стенке трубы
s ![]() = 100 МПа, s
= 100 МПа, s ![]() = 20 МПа,
= 20 МПа,
s ![]() = 200 МПа, s
= 200 МПа, s ![]() = 200 МПа,
= 200 МПа,
D s ![]() = 0 МПа, D s
= 0 МПа, D s ![]() = 0 МПа,
= 0 МПа,
D s ![]() = 0 МПа, D s
= 0 МПа, D s ![]() = 0 МПа,
= 0 МПа,
4) сезон 4: наработка изменяется в интервале D Т1 + D Т2+ D Т3 £ Т £ D Т1 + D Т2 + D Т3 + + D Т4 = Т * , что соответствует номинальным напряжениям в стенке трубы
s ![]() = 200 МПа, s
= 200 МПа, s ![]() = 100 МПа,
= 100 МПа,
s ![]() = 250 МПа, s
= 250 МПа, s ![]() = 250 МПа,
= 250 МПа,
D s ![]() = 0 МПа, D s
= 0 МПа, D s ![]() = 0 МПа,
= 0 МПа,
D s ![]() = 0 МПа, D s
= 0 МПа, D s ![]() = 0 МПа,
= 0 МПа,
Здесь индексы "е" и " i " соответствуют внешней и внутренней образующим сечения стенки цилиндрического сегмента.
П.4.2.2. Формирование классов по типам дефектов:
a) продольные (осевые) трещины на внешней образующей трубы;
b) поперечные (кольцевые) трещины на внешней образующей трубы;
c) продольные (осевые) трещины на внутренней образующей трубы;
d ) поперечные (кольцевые) трещины на внутренней образующей трубы.
П.4.2.3. Общее число классов образуется числом возможных сочетаний первой и второй группы: 4 ´ 4= 16.
1.2.4. Парциальные вероятности реализации событий первой группы:
Н ![]() = 0,2,
= 0,2,
Н ![]() =
0,15,
=
0,15,
Н ![]() =
0,5,
=
0,5,
Н ![]() =
0,15,
=
0,15,
причем ![]() .
.
Парциальные вероятности событий второй группы:
Н ![]() = 0,45,
= 0,45,
Н ![]() =
0,35,
=
0,35,
Н ![]() =
0,08,
=
0,08,
Н ![]() =
0,02,
=
0,02,
причем ![]() .
.
Парциальные вероятности реализации событий класса Ф ij ( i - по 1 группе, j - по второй группе):
Hij (Ф ij )=Н ![]() Н
Н ![]() ,
,
Н11 = Н ![]() Н
Н ![]() ,=0,2 ´ 0,45=0,0900, H 21 = Н
,=0,2 ´ 0,45=0,0900, H 21 = Н ![]() Н
Н ![]() ,=0,15 ´ 0,45=0,0675
,=0,15 ´ 0,45=0,0675
H 12 = Н ![]() Н
Н ![]() ,=0,2 ´ 0,35=0,0700,
Н22 = Н
,=0,2 ´ 0,35=0,0700,
Н22 = Н ![]() Н
Н ![]() ,=0,15 ´ 0,35=0,0525
,=0,15 ´ 0,35=0,0525
H 13 = Н ![]() Н
Н ![]() ,=0,2 ´ 0,08=0,0160, Н23
= Н
,=0,2 ´ 0,08=0,0160, Н23
= Н ![]() Н
Н ![]() ,=0,15 ´ 0,08=0,0120
,=0,15 ´ 0,08=0,0120
H 14 = Н ![]() Н
Н ![]() ,=0,2 ´ 0,02=0,0040, Н24
= Н
,=0,2 ´ 0,02=0,0040, Н24
= Н ![]() Н
Н ![]() ,=0,15 ´ 0,02=0,0030
,=0,15 ´ 0,02=0,0030
Н31 = Н ![]() Н
Н ![]() ,=0,5 ´ 0,45=0,2250, H 41 = Н
,=0,5 ´ 0,45=0,2250, H 41 = Н ![]() Н
Н ![]() ,=0,15 ´ 0,45=0,0675
,=0,15 ´ 0,45=0,0675
H 32 = Н ![]() Н
Н ![]() ,=0,5 ´ 0,35=0,1750, Н41
= Н
,=0,5 ´ 0,35=0,1750, Н41
= Н ![]() Н
Н ![]() ,=0,15 ´ 0,35=0,0525
,=0,15 ´ 0,35=0,0525
H 33 = Н ![]() Н
Н ![]() ,=0,5 ´ 0,08=0,0160, Н41
= Н
,=0,5 ´ 0,08=0,0160, Н41
= Н ![]() Н
Н ![]() ,=0,15 ´ 0,08=0,0120
,=0,15 ´ 0,08=0,0120
H 34 = Н ![]() Н
Н ![]() ,=0,5 ´ 0,02=0,0040, Н41
= Н
,=0,5 ´ 0,02=0,0040, Н41
= Н ![]() Н
Н ![]() ,=0,15 ´ 0,02=0,0030
,=0,15 ´ 0,02=0,0030
Выделенные жирным шрифтом парциальные риски показывают, что вклад в суммарную вероятность событий данных классов будет заведомо более существенным, так что анализом остальных случаев можно пренебречь. Вместе с тем, если с физической точки зрения ясно, что более опасны трещины осевые, то при учете методами условных функций надежности случайной реализации однородных напряжений по четырем сезонам (с различной вероятностью реализации этих режимов нагружений) оказывается, что вклад кольцевых трещин при некоторых сезонах весьма существенно влияет на суммарную вероятность отказа. В дальнейшем можно перенумеровать классы пространства состояний в общую совокупность: Ф j , j = 1,2,...,16.
П. 4.3. Расчет роста усталостных трещин и определение границ допустимых областей по начальным размерам трещин
П.4.3.1. При расчете роста поверхностных трещин в стенке трубопровода предполагаем, что форму трещины можно аппроксимировать полуэллипсом с размерами полуосей а (глубина) и b (длина). Причем, предполагается, что в процессе роста полуэллиптическая форма трещины не изменяется.
П.4.3.2. Размеры трещины являются функциями временного параметра t (а = a ( t ), b = b ( t )), соответствующего наработке или текущему эксплуатационному периоду участка ЛЧМГ. В некоторый момент времени, принятый за начальный to , размеры трещины равны начальным: a ( t 0 ) = a 0 , b ( t 0 ) = b 0 . В случае усталостного нагружения удобно вести расчеты роста трещины в зависимости от наработки N - числа циклов нагружения, с последующим пересчетом на календарную наработку t = t ( N ).
П.4.3.3. Уравнения роста усталостных полуэллиптических трещин / 6, 7/.
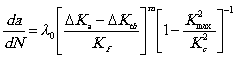 (П. 4.1)
(П. 4.1)
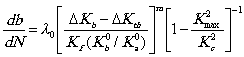
Здесь D Ка, D К b - размахи коэффициентов интенсивности напряжений соответственно в точках А и В фронта ( см. рис. П. 4.1); D К th - пороговое значение коэффициента интенсивности; Kmax - максимальное значение КИН, соответствующее максимальному номинальному напряжению цикла в стенке трубы; Кс - критическое значение КИН; Kf - сопротивление накоплению повреждений.
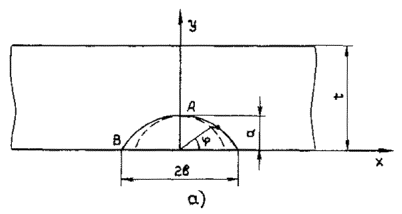
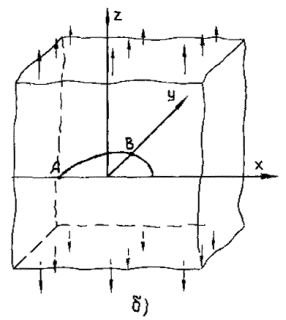
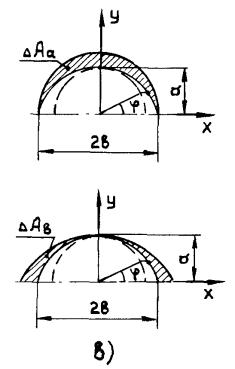
Рис. П.4.1. Рост усталостной трещины
П.4.3.4. Коэффициенты интенсивности напряжений Ка и К b на концах полуосей трещины. Для расчета этих величин обычно применяют один из следующих пяти методов: метод конечных элементов (МКЭ) с использованием методик виртуального роста трещины, J-интегралов и т.д. / 4, 8/; метод весовых функций / 9/; метод объемных сил / 5/; метод граничных интегральных уравнений / 10/; метод упругих пружин Раиса и Леви / 11/.
Рассмотрим пространственное деформирование участка трубопровода под действием системы изгибающих моментов М j растягивающих мембранных усилий Nk , внутреннего давления р и системы сосредоточенных сил Pi , линия действия которых пересекает ось трубопровода ( см. рис. П. 4.2). Пусть в стенке трубопровода имеется несквозная окружная или осевая полуэллиптическая трещина ( рис. П. 4.3). Будем различать также наружные ( рис. П. 4.3, а, б) и внутренние ( рис. П. 4.3, в, г) трещины. Размеры трещины а и b сопоставимы с толщиной стенки t . Величина t много меньше радиуса оболочки R . Требуется с максимально возможной точностью определить распределение КИН вдоль фронта трещины. В такой постановке задача может быть решена с использованием прямого метода расчета, заключающегося в целесообразной дискретизации трубчатого образца с трещиной и численном определении искомых величин одним из вышеперечисленных методов.
Вторая задача состоит в нахождении КИН полуэллиптической трещины в трубчатом элементе с заданным распределением напряжений по ее берегам. Эта задача представляет собой типичную 3-х мерную задачу механики разрушения. При ее решении учтем также, что в реальных магистральных газопроводах толщина стенки t много меньше радиуса R, а окружные s q q и осевые s z напряжения распределены по толщине стенки трубопровода практически линейно. Кроме того отметим, что в силу малости характерных размеров трещины по отношению к радиусу кривизны R, влияние последнего на КИН можно не учитывать. В такой постановке можно использовать результаты работы / 4/, в которой для пластины конечной толщины получены КИН полуэллиптической трещины с линейным распределением напряжений на ее берегах. Эта задача решена в работе / 4/ на основе полномасштабного 3-х мерного конечно-элементного анализа. Расчет проводился на довольно мощных сетках (до 6500 степеней свободы) при широком варьировании геометрии трещины. Результаты расчета КИН аппроксимировались затем полиномами. Окончательное решение имеет вид:
K1 = (St + HSb)( p a/Q)1/2F(a/t, a/b, b/c, f ),
Q = 1 + 1,464 (a/b)1,65,
F = [M1 + M2(a/t)2 + М 3 ( а /t)4] f f g,
M1 = 1,13 - 0,09 (a/b),
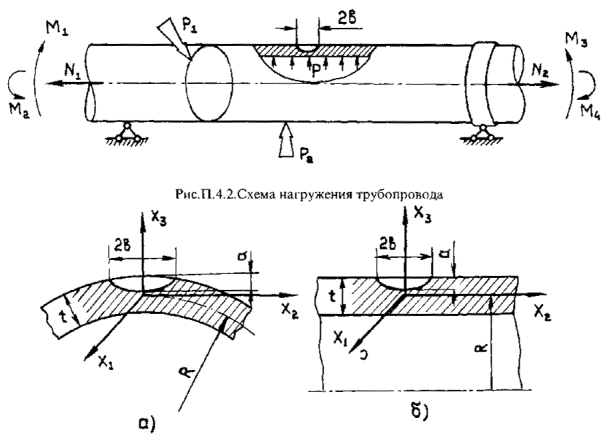
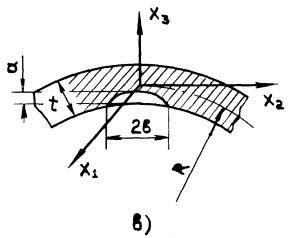
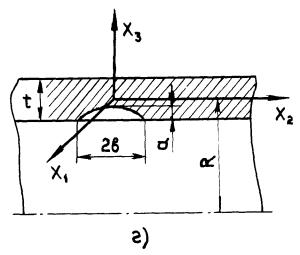
Рис. П.4.3. Полуэллиптические трещины в стенке трубопровода
М 2 ![]() ,
( П . 4.2)
,
( П . 4.2)
М 3 ![]() 14 (1,0-a/b)24,
14 (1,0-a/b)24,
g = 1 + [0,1 + 0,35(a/t)2](1-sin f )2,
Sb = ( s 1 - s 2 )/2,
St = ( s 1 + s 2 )/2
Здесь a , b - глубина и полудлина полуэллиптической трещины; f - полярный угол на фронте, отсчитываемый от поверхности пластины. При исследовании осевых трещин под s 1 , и s 2 следует понимать величины окружных напряжений сгее соответственно на поврежденной и неповрежденной поверхностях образца. При расчете окружных трещин обозначения s 1 и s 2 относятся к осевому напряжению s z . Функция f f углового распределения для эллиптической трещины имеет вид
f f = [(a/b)2cos2 + sin2 f ]1/4. (П. 4.3)
Для функции Н( f ) получена следующая аппроксимация /4/
H=H1 + (H2 - H1)sinp( f ),
р = 0,2 + a/b + 0,6a/t, ( П . 4.4)
H1 = 1 - 0,34a/t - 0,11a/b(a/t),
Н 2 = 1 + G1(a/t) + G2(a/t)2, ( П . 4.5)
G1 =-1,22 - 0,12a/b,
G2 = 0,55 - 1,05(a/b)0,75 + 0,47(a/b)1,5. (П.4.6)
Решения (П. 4.2) - (П. 4.6) справедливо при 0 < a/b < 1,0, 0 £ a / t £ 1,0, b / c < 0,5, 0 £ f £ p . При a/t £ 0,8 точность аппроксимации составляет ± 5% При a/t > 0,8 точность аппроксимации не оценивалась, но решение в этом интервале подтверждается оценками, основанными на эквивалентных сквозных трещинах / 4/. Можно использовать также решение / 5/, полученное методом объемных сил (погрешность < 1%).
Обратим внимание, что внутренние трещины ( рис. П. 4.3, в, г) качественно отличаются от внешних трещин ( рис. П. 4.3, а, б) наличием дополнительной нагрузки от газа, проникающего в полость трещины. Добавку в КИН от этого эффекта следует определять по формулам (П. 4.2) - (П. 4.6), принимая Sb =0, St = p , где р - величина внутреннего давления в трубопроводе.
П.4.3.5. Выбор и обоснование параметров уравнений роста усталостных трещин. Для проведения расчета распространения усталостных трещин в реальных трубопроводных конструкциях необходимо предварительно определить константы Kf , Kth , Кс, m , входящие в уравнения ( П. 4.1). Эти константы по сути являются характеристиками циклической трещиностойкости материала. Они должны вычисляться на основе кинетических диаграмм усталостного разрушения материала, представляющих собой экспериментальные зависимости скорости роста однопараметрической трещины от КИН. Методика проведения соответствующих испытаний с подробными рекомендациями по выбору образцов и схем нагружения изложена в / 10/. Там же приведен алгоритм обработки результатов эксперимента вплоть до построения искомой кинетической диаграммы.
Оценки для параметров трещиностойкости разных марок сталей сильно различаются как в отношении качества материала, так и в результате разных экспериментальных подходов к их определению. Для порогового значения КИН оценки лежат в пределах 2... 10 МПа × м1/2 /12/, для критических КИН - в пределах 40... 200 и выше МПа × м1/2 / 12, 13/. Для высокопрочных трубопроводных сталей с большим процентным содержанием ванадия и т. п. следует, при отсутствии собственных расчетно-экспериментальных оценок, принимать значения параметров трещиностойкости, соответствующие верхним пределам, т.е. Kth = D Kth » 5...10 МПа × м1/2, K 1 c 150,.. 200 МПа × м1/2. Параметры сопротивления накоплению повреждений - Ks , Kf - могут быть оценены по имеющимся данным о начальных скоростях роста трещин в данном материале и сопоставлении различных моделей уравнений роста. Сравнивая модели Пэриса и В.В. Болотина для момента страгивания трещины, получим оценки типа
Kf » ( l f /C)1/mf,
где С - константа в уравнении Пэриса, l f - характерный размер микроструктуры материала, ниже которого перестают действовать предположения линейной механики разрушения (размер зерна). Приближенные оценки для величин Kf, Ks лежат в пределах 50,.. 100 МПа × м1/2 для высокопрочных сталей.
П.4.3.6. Моделирование роста трещин прекращается по достижении размером а критической величины ( a * ( t * ) = h , где h - толщина стенки оболочки), или переходе трещины в состояние неустойчивого роста по одной или двум полуосям (например, нарушение в момент времени t * * условия ( Ka / K 1 c )2 + (К b /K1c)2 < 1). Критические времена t * (или t * * ) являются на данном этапе основной итоговой информацией и соответствуют времени до разгерметизации трубопровода.
4.3.7. Определение границ допустимых областей.
Для определения границ допустимых
областей начальных размеров трещин а0 и b 0 воспользуемся
следующим алгоритмом. При фиксированном типе размещения трещины в теле трубы
граница допустимой области W s в пространстве размеров трещин и времени ( a / h , b / h , t / T )
представляет собой двумерную поверхность Г = Г(а ![]() , b
, b ![]() ,Т), где а
,Т), где а ![]() , b
, b ![]() имеют смысл начальных
размеров трещины, которая по достижении значения t
= Т насквозь прорастет стенку трубопровода (а(Т) = h) или в некоторый момент
времени t * * £ Т станет неустойчивой / 6, 7/. Здесь Т -
допустимое значение наработки, назначенный срок службы и т.п.
имеют смысл начальных
размеров трещины, которая по достижении значения t
= Т насквозь прорастет стенку трубопровода (а(Т) = h) или в некоторый момент
времени t * * £ Т станет неустойчивой / 6, 7/. Здесь Т -
допустимое значение наработки, назначенный срок службы и т.п.
Условие принадлежности значений начальных размеров трещины области допустимых состояний в момент времени t = 0 с учетом типа размещения трещины 11 oc имеет вид:
W s 0 = W s { a 0 , b 0 ½ а(а0, t ) < h, а(а0, t ) < а * * , b ( b 0 , t ) < b * * ;
t Î [0,t * ]; 11oc} ( П . 4.7)
Здесь параметр времени t * определяет заданный период эксплуатации (например, t * = Т - назначенный срок службы).
Для построения границ допустимых областей организуется следующий итерационный процесс. Зададим начальные размеры дефекта а0, b 0 . Интегрируя уравнения роста трещины, вычислим ее конечные значения в момент времени t = t * . Проверим выполнение условий 4.3.6. При достижении, с требуемой точностью вычислений, глубиной трещины размера толщины стенки оболочки за заданное время или при нарушении условия устойчивости вычисления роста прекращаются, а начальные значения размеров трещины запоминаются. В противном случае в начальные значения вносится соответствующая поправка, и вычисления продолжаются. Процесс вычислений продолжаем до получения достаточного для удовлетворительной аппроксимации границы числа точек в интервале [0, h ] ´ [0, ¥ ]. Примеры построения допустимых областей по начальным размерам трещины и заданных уровне нагружения и назначенном сроке службы приведены на рис. П. 4.4 / 2/.
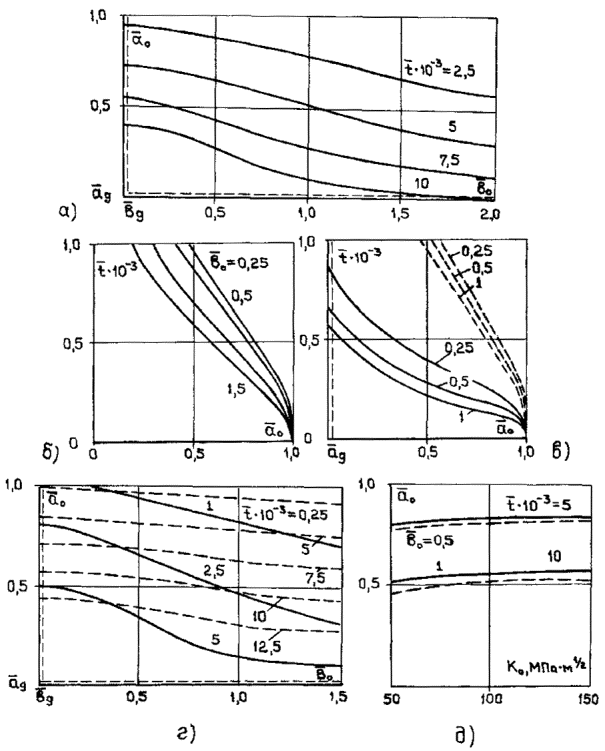
Рис. П.4.4. Примеры построения допустимых областей по начальным размерам трещин и заданном уровне нагружения и назначенном сроке службы
П.4.4. Оценка показателей надежности по критерию роста усталостных трещин
П.4.4.1. Оценка вероятности распределения времени до разгерметизации и интенсивности отказов. Алгоритм расчета основан на применении метода наибольшего правдоподобия для получения оценок распределений экстремальных значений из выборок случайных величин / 14/.
П.4.4.2. Для оценки надежности системы в целом необходимо определить функции вероятности F ( h , t ) сквозного прорастания единичного наугад взятого дефекта к моменту времени t .
Рассмотрим Ns начальных трещин, размеры которых подчиняются
экспоненциальному (для полуоси а) и усеченному нормальному (для отношения u = b / a )
законам распределения. Пусть j-й наугад взятый дефект прорастает до сквозного
за некоторое время tj ( h ).
Пусть F ( h , t )
- вероятность того, что наугад взятый дефект прорастет до сквозного за время t < t . Введем случайную величину x ( h ) = min ( t 1 , t 2 ,..., tN ![]() ). Функция
распределения х определяется следующим образом:
). Функция
распределения х определяется следующим образом:
Fx ( h , t )
= P [ x ( h )
< t ] = 1- P [ t 1 ( h )> t , t 2 ( h ) > t ,.., t N ![]() ( h )> t ] = 1-[1- F ( h , t )] N
( h )> t ] = 1-[1- F ( h , t )] N ![]() . (П. 4.8)
. (П. 4.8)
В этом случае распределение Fx ( h , t ) представляет собой известное трехпараметрическое распределение Вейбулла /14/
Fx(h,t) = 1- ехр 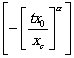 ,
,
x0 £ t £ ¥ , x > 0, a > 0. (П.4.9.)
Процесс моделирования организуем
следующим образом. Моделируем Ns размеров начальных глубин и длин а0,
b 0 полуэллиптических
трещин. Проводим цензурирование выборки по критерию принадлежности исключаемых
значений допустимой области. Выбираем из полученных трещин трещину с
максимальной глубиной. Вычисляем время ее прорастания до сквозной и запоминаем
значение t ![]() . Процедуру выбора повторяем. Полученная усеченная выборка
объема Ns принадлежит некоторой генеральной совокупности
распределения Вейбулла. Таким образом, мы моделируем новую выборку Ns
минимальных времен прорастания трещин, находящихся вне допустимой области, t
. Процедуру выбора повторяем. Полученная усеченная выборка
объема Ns принадлежит некоторой генеральной совокупности
распределения Вейбулла. Таким образом, мы моделируем новую выборку Ns
минимальных времен прорастания трещин, находящихся вне допустимой области, t ![]() ( j =1... Ns ). Заключительным этапом вычислительного эксперимента
является обработка полученной выборки t
( j =1... Ns ). Заключительным этапом вычислительного эксперимента
является обработка полученной выборки t ![]() ( h ), ( j =1... Ns ) методом наибольшего правдоподобия для получения оценок
для параметров распределения Вейбулла х0, Хс и a , Определив оценки
( h ), ( j =1... Ns ) методом наибольшего правдоподобия для получения оценок
для параметров распределения Вейбулла х0, Хс и a , Определив оценки ![]() 0,
0, ![]() с,
с, ![]() , функцию распределения времен отказов найдем по формуле
, функцию распределения времен отказов найдем по формуле
F(h,t)
= 1-exp 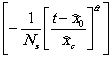 .
( П . 4.10)
.
( П . 4.10)
Для получения параметров распределения Вейбулла применим метод наибольшего правдоподобия, который дает несмещенные и эффективные оценки этих параметров. Оптимизационный алгоритм основан на применении симплекс-метода / 15/.
П.4.4.3. Оценка показателей надежности.
Пусть расчетная ЛЧМГ разбита на NL у участков по конструктивным признакам, а пространство состояний участков трубопровода состоит из совокупности классов {Ф j }.
При введенных предположениях вероятность безотказной работы за время t оценивается по формуле
R(t)=exp 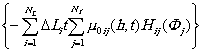 ,
( П .
4.11)
,
( П .
4.11)
где m 0 ij - математическое ожидание числа начальных трещин на i-м участке трубопровода, Fij ( h , t ) - функция распределения глубины трещины к моменту времени t , Hij (Ф j ) - парциальный риск возникновения опасной ситуации класса Ф j на i-том участке.
П.4.4.4. Другой алгоритм оценки надежности трубопровода по критериям конструкционной целостности и герметичности основан на применении методов Монте-Карло и предназначен для максимального подавления влияния на расчеты фактора неполноты и недостоверности исходной информации. При таком расчете учитывается тот факт, что многие параметры, существенно влияющие на поведение трубопровода, обладают большой изменчивостью, а, следовательно, конфигурация и размеры допускаемой области W s , также носят случайный характер.
П.4.5. Пример расчета. Ограничимся только осевой внешней трещиной и четырьмя сезонами. Тогда классов в пространстве состояний будет 4. Проводим расчет роста трещин, моделирование и оценку параметров распределений.
4.5.1. Расчетные показатели параметров вероятностей распределений по П.4.4.2. для четырех классов будут следующими:
t 10 = 5 сут. t 1 c = 200 сут. a 1 = 2,1;
t 20 = 6 сут. t 2 c = 150 сут. a 2 = 2,3;
t 30 = 3 сут. t 3 c = 250 сут. a 3 = 2,3;
t 40 = 10 сут. t 4 c = 75 сут. a 4 = 2,2;
4.5.2. Вычислим вероятности реализации событий (прорастание трещины до сквозной) за время t = 365 сут (1 год) по формуле типа п. 4.4.2:
Fi(t)=1-exp 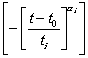
F 1 ( t ) = 1 - ехр( - ((365 - 5)/200))2.1) = 0,9678116
F 2 ( t ) = 1 - ехр( - ((365 - 6)/150))2.3) = 0,9994141
F 3 ( t ) = 1 - ехр( - ((365 - 3)/250))2.3) = 0,90390585
F 4 ( t ) = 1 - ехр( - ((365 - 10)/75))2.2) » 1,0
П.4.5.3. Вычислим суммарную надежность по трассе длиной D L = 1 км, полагая математическое ожидание числа начальных дефектов m = const = 1/1год/1км. При этом парциальные вероятности реализации событий 4-х классов берем из первой группы п. 1.2.4:
R(365)
= exp( -1 ´ 1 ´ 1 ´ ![]() ) = exp (- (0,9678116 ´ 0,2 + 0,9994141 ´ 0,15 + 0,90390585 ´ 0,5 + 1 ´ 0,15)) = exp (- ( 0,19356 + 0,14991
+ 0,45198 + 0,15)) = 0,38850
) = exp (- (0,9678116 ´ 0,2 + 0,9994141 ´ 0,15 + 0,90390585 ´ 0,5 + 1 ´ 0,15)) = exp (- ( 0,19356 + 0,14991
+ 0,45198 + 0,15)) = 0,38850
Полученный результат позволяет сделать следующие заключения: по 2-му и 4-му классам состояний вероятности прорастания трещин до сквозных практически близки к 1; вместе с тем реализации этих классов состояний имеют вероятности 0,15 и поэтому суммарная вероятность безотказной работы участка трубопровода за год будет определяться реализацией 1-го и 3-го классов состояний главным образом. Однако, если с вероятностью 1 в течение года будет реализовываться состояние 4-го класса, то надежность участка снизится до 0,3679.
Список использованных источников
1. Программно-методический комплекс для расчета линейных частей магистральных трубопроводов, прокладываемых в сложных природно-климатических условиях / ИМАШ АН СССР. 1989. 106 с.
2. Силкин В.М. , Ковех В.М. , Нефедов С. В. , Панов U . Ю. Оценка безопасности газопровода по критерию трещиностойкости // Надежность газопроводных конструкций. М.: ВНИИгаз. 1990, С. 11-23
3. Разработка метода расчетного прогнозирования герметичности и трещиностойкости тонкостенных трубчатых элементов / ИМАШ АН СССР. 1989. 119 с .
4. Shiratori M., Miyoshi Т ., Tanikawa К . Analysis of stress intensity factors for surface cracks subjected to arbitraly distributed surface stresses. Analysis and application of influence coefficients for flat plates with a semi-elliptical surface crack // Trans. JSME, 1986. Vol. 52. N 474. P. 390-398.
5. Kawahara M., Kurihara M. Fatigue crack growth from surface flow // Proc. 4th Int. Conf. Fracture. Waterloo, Canada. 1977. Vol .2. P . 1361-1373.
6. Болотин В. В. Уравнения роста усталостных трещин // Механика твердого тела. 1983. № 4. С. 153-160,
7. Болотин В.В. Ресурс машин и конструкций. М.: Машиностроение. 1990, 480 с .
8. Dai Y., Rodig M., Altes J. Calculation of the stress intensity factor for a partial circumferentially cracked tube loaded in bending by using the shell line-spring model // Fatigue Fract. Engng Mater, struct., 1991. Vol. 14. N 1. P. 11-23.
9. Fett Т ., Munz D., Newman J. Local stress intensity factors for surface cracks in plates under power-shaped stress distributions // Engng Fracture Mech. Vol.36. 1981. P . 647-651.
10. РД 50-345-82. Методические указания. Расчеты и испытания на прочность. Методы механических испытаний металлов. Определение характеристик трещиностойкости (вязкости разрушения) при циклическом нагружении. - Ввод. 01.01.83. М.: Изд-во стандартов, 1983. 95 с.
11. Экспериментальная механика // Под. ред. А. Кабаяси. М.: Мир. 1990, Т. 2. 551 с.
12. Хеллан К. Введение в механику разрушения. Пер. с англ. М.: Мир. 1988. 364 с.
13. Черепанов Г. П. Механика хрупкого разрушения. М.: Наука. 1974. 640с.
14. Лидбеттер М., Ротсен X., Линдгрен Г. Экстремумы случайных последовательностей и процессов. Пер. с англ. М.: Мир. 1989. 392 с.
15. Химмельблау Д. Прикладное нелинейное программирование. Пер. с англ. М.: Мир. 1975. 534 с.
ПРИЛОЖЕНИЕ 5. УЧЕТ СРОКА СЛУЖБЫ ПРИ РАСЧЕТЕ ТОЛЩИНЫ СТЕНКИ ТРУБОПРОВОДА
В процессе эксплуатации на трубопровод действует внутреннее давление p ( t ), которое представляет собой случайную функцию времени. Характер ее изменения таков, что силами инерции при определении напряжений в трубе можно пренебречь, при этом максимальные напряжения, возникающие в трубопроводе, определяются выражением:
S(t)=Kp= ![]() ,
( П .5.1)
,
( П .5.1)
где DH -наружный диаметр труб, d - толщина стенки трубы.
Внутреннее давление в газопроводе можно рассматривать как стационарный нормальный процесс с корреляционной функцией, аппроксимируемой формулой
Kp( t )= ![]() ,
(П.5.2)
,
(П.5.2)
где s Р - стандарт функции p ( t ). В этом случае, учитывая формулу (П. 5.1), получаем
|
|
|
(П. 5.3) |
где s s s s стандарты функций S ( t ) и S ( t )
Принимаем, что несущая способность материала труб определяется пределом прочности на разрыв и является случайной величиной с известным законом распределения.
Долговечность труб тесно связана с их надежностью P ( t ), под которой понимают вероятность наступления события, что за время Т максимальное значение функции S ( t ) ни разу не превысит уровня несущей способности R . Принимая данные теории выбросов случайной функции за случайный уровень, а также то, что мы рассматриваем случай, когда появление последовательных выбросов можно считать независимыми "редкими" событиями, т.е. подчиняющимися закону Пуассона, получим функцию надежности в виде
P(t)=exp 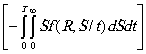 ( П . 5.4)
( П . 5.4)
Здесь ![]() - производная функция
S ; f (...) - совместная плотность
распределения R и S
в момент времени t .
- производная функция
S ; f (...) - совместная плотность
распределения R и S
в момент времени t .
Считая, что несущая способность материала трубы R распределена по нормальному закону, из формулы (П. 5.4) по аналогии получим выражение для функции надежности:
P(t)=exp 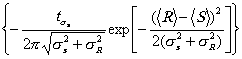 ,
( П . 5.5)
,
( П . 5.5)
где < R >, < S > - математические ожидания R и S.
Среднюю долговечность труб ![]() по известной функции
надежности ( П. 5.5) можно
определить из выражения
по известной функции
надежности ( П. 5.5) можно
определить из выражения
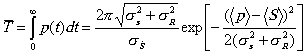 ,
(П. 5.6)
,
(П. 5.6)
Введем безмерные параметры: ![]() аналог коэффициента
запасов;
аналог коэффициента
запасов;
![]() ,
, 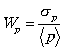 - коэффициенты
изменчивости случайных величин R и р;
- коэффициенты
изменчивости случайных величин R и р;
g = a / b , Т * =Т b - безразмерная долговечность. Подставляя эти выражения в выражение (П. 5.6), с учетом формулы (П. 5.3) получим окончательную формулу для определения долговечности
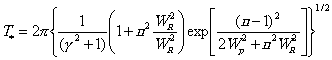 (П.5.7)
(П.5.7)
При проектировании газопроводов важное место занимают параметры, которые обеспечивают надежную и длительную эксплуатацию. Толщину стенки трубопровода при заданных средних < R >, < p > можно рассчитать из выражения
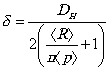 (П. 5.8)
(П. 5.8)
Задаваясь средней долговечностью ![]() , характеристиками нагрузок a , b ,
из выражения (П. 5.7)
определим коэффициент запаса n , а из выражения (П. 5.8) -
толщину стенки газопровода.
, характеристиками нагрузок a , b ,
из выражения (П. 5.7)
определим коэффициент запаса n , а из выражения (П. 5.8) -
толщину стенки газопровода.
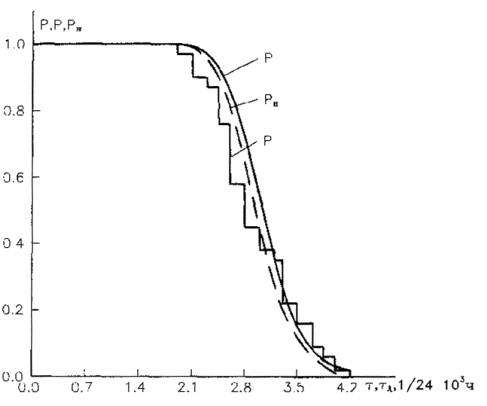
Рис.П.5.1. График функции надежности
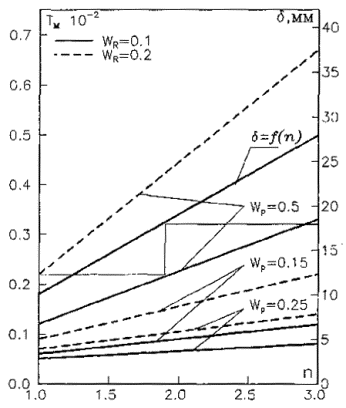
Рис. П. 5.2. График зависимости долговечности от коэффициента запаса и толщины стенки
g = 0,05; DH = 1420 мм; < R > = 600 МПа; <р> = 7,5 МПа
В качестве примера применения настоящей методики расчета на рис. П. 5.2 приведена номограмма, которая представляет собой графики зависимости безразмерной средней долговечности от коэффициента запаса при различных значениях параметров WR , Wp , g , и график зависимости от этого коэффициента толщины стенки трубы. Выразив долговечность через Т * , механические характеристики материала < R >, WR и нагрузку <р>, Wp, можно по номограмме определить толщину стенки d .
Таким образом, зная статистические характеристики нагрузки на трубопровод и данные о разбросе механических свойств материала, можно проектировать трубопровод с учетом необходимой долговечности, что позволит закладывать требуемый уровень надежности уже на стадии проектирования.
СОДЕРЖАНИЕ
|
1. Назначение, структура и область применения . 2 1.1. Технико-экономическая постановка задачи . 2 1.2. Структура Методических рекомендаций . 2 2. Основы стандартизации и нормирования показателей надежности сложных технических систем .. 3 2.1. Основные понятия . 3 2.2. Показатели надежности . 4 2.3. Применение моделей и методов теории надежности при проектировании ЛЧМГ . 6 3. Методика расчета показателей конструктивной надежности линейных частей магистральных газопроводов . 9 3.1. Основные характеристики конструкции ЛЧМГ и трассы газопровода в целом .. 9 3.2. Нагрузки и воздействия . 10 3.3. Классификация отказов и предельных состояний . 12 3.4. Требования к построению расчетных схем для оценки напряженно-деформированного состояния участка газопровода . 15 3.5. Формирование расчетных участков . 15 3.6. Формирование пространства состояний расчетного участка . 16 3.7. Перечень и структура нормируемых показателей надежности . 17 3.8. Методы расчета показателей надежности . 17 Перечень программных продуктов, предназначенных для расчетного прогнозирования показателей надежности и долговечности линейных частей магистральных газопроводов . 19 Комментарии к "методическим рекомендациям по расчетам конструктивной надежности магистральных газопроводов" . 21 1. Комментарий к п. 3.2. Нагрузки и воздействия . 22 1.1. Нормативные расчеты для стандартных условий . 22 1.2. Расчеты для нестандартных условий . 23 Список использованных источников . 25 2. Комментарий к п. 3.3. Классификация отказов и предельных состояний . 26 2.1. Критерии разрушения элементов трубопроводных конструкций при статическом нагружении . 26 Список использованных источников . 27 2.2. Критерии прочности и методы расчета элементов трубопроводов при малоцикловом нагружении . 27 Список использованных источников . 28 2.3. Критерии прочности и методы расчета элементов трубопроводов при много цикловом нагружении . 28 Список использованных источников . 29 2.4. Критерии трещиностойкости элементов трубопроводов по отношению к усталостным трещинам .. 29 Список использованных источников . 30 3. Комментарий к п. 3.4. Требования к построению расчетных схем для оценки напряженно-деформированного состояния участка газопровода . 30 4. Комментарий к п. 3.5. Формирование расчетных участков . 32 5. Комментарий к п. 3.6. Формирование пространства состояний расчетного участка . 33 6. Комментарий к п. 3.8. Методы расчета показателей надежности . 34 6.1. Применение вероятностных моделей при расчете трубопроводов . 34 Список использованных источников . 35 6.2. Применение вероятностных моделей для оценки показателей надежности трубопроводов по критерию трещиностойкости. Последовательность выполнения расчетов . 35 ПРИЛОЖЕНИЯ .. 36 Приложение 1. Оценка несущей способности трубопроводов, прокладываемых в промерзающих пучинистых грунтах . 36 П. 1.1. Предельные состояния трубопроводов при контактном взаимодействии с промерзающим грунтом .. 36 П. 1.2. Взаимодействие трубопровода с единичным бугром пучинистого грунта . 38 П. 1.3. Построение областей предельно допустимых размеров бугров пучения . 39 Список использованных источников . 40 Приложение 2. Формирование пространства состояний расчетного участка . 40 Приложение 3. Оценка показателей надежности линейных частей магистральных трубопроводов, прокладываемых в промерзающих пучинистых грунтах . 45 П. 3.1. Постановка задачи об оценке показателей надежности протяженных конструкций . 45 П.3.2. Оценка условной безопасности S a методом статистического моделирования . 46 П.3.3. Обсуждение численных результатов . 48 Приложение 4. Расчет показателей надежности и долговечности по отношению к критическим отказам, связанным с ростом усталостных трещин, в надземных газопроводах при действии ветровой нагрузки и просадке опор . 53 П.4.1. Формирование расчетных участков . 53 П.4.2. Формирование пространства состояний расчетного участка . 53 П. 4.3. Расчет роста усталостных трещин и определение границ допустимых областей по начальным размерам трещин . 55 П.4.4. Оценка показателей надежности по критерию роста усталостных трещин . 61 Приложение 5. Учет срока службы при расчете толщины стенки трубопровода . 63 |