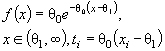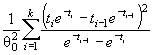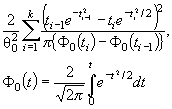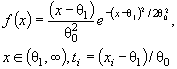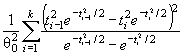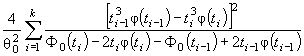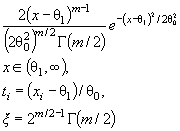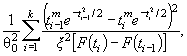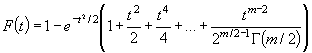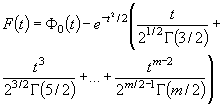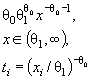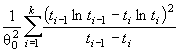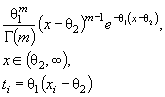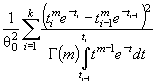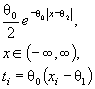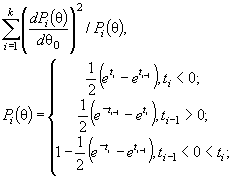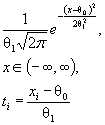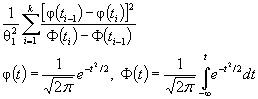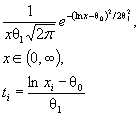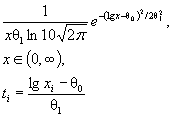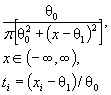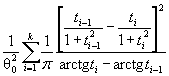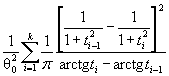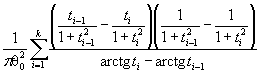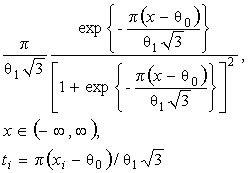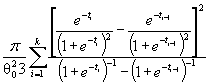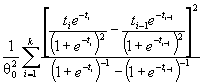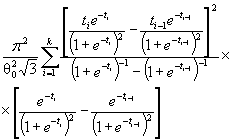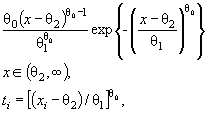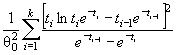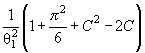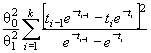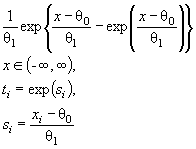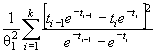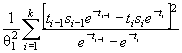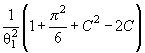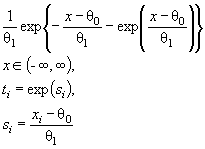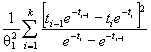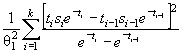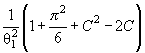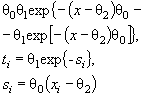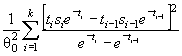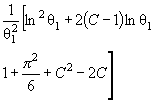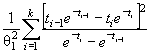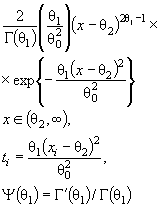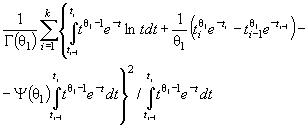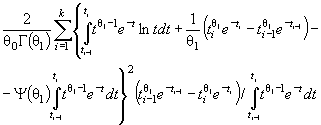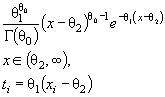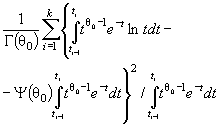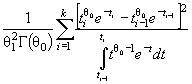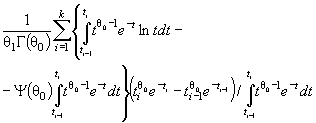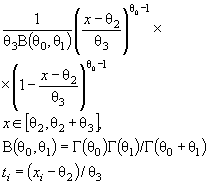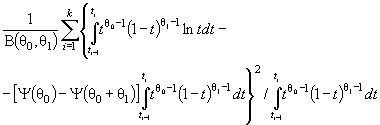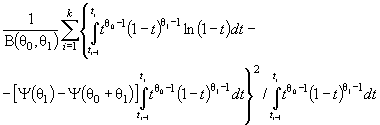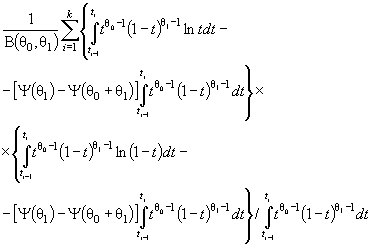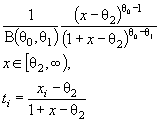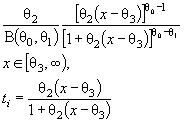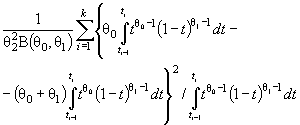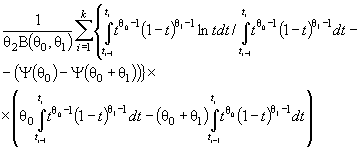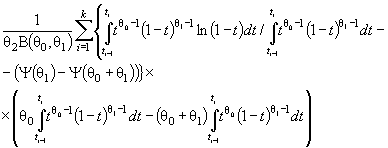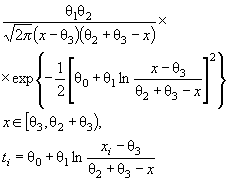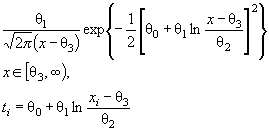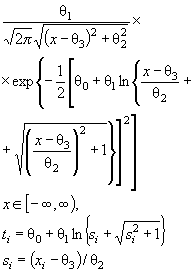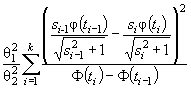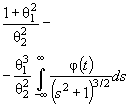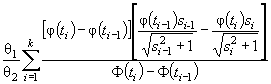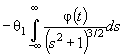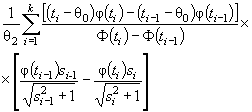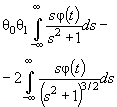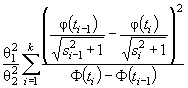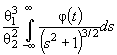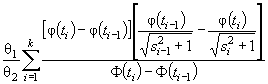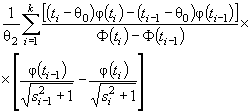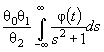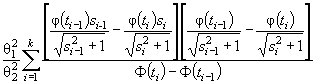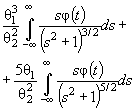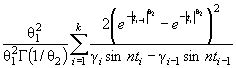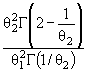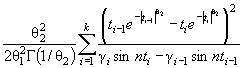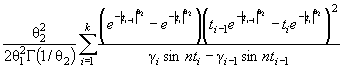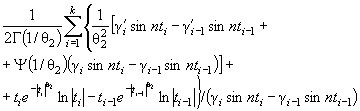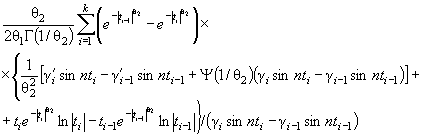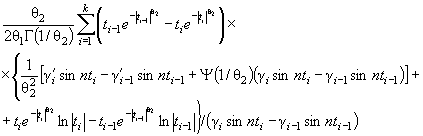Р 50.1.033-2001 Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат
Р 50.1.033-2001
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
|
Прикладная статистика ПРАВИЛА ПРОВЕРКИ СОГЛАСИЯ ОПЫТНОГО РАСПРЕДЕЛЕНИЯ С ТЕОРЕТИЧЕСКИМ Часть 1 Критерии типа хи-квадрат Applied
statistics. Rules of check of experimental and theoretical distribution of
the consent |
Дата введения 2002-07-01
ГОССТАНДАРТ РОССИИ
Москва
Содержание
|
1 Область применения 2 Теоретические основы рекомендаций 2.1 Общие положения 2.2 Критерии типа χ2 при простых гипотезах 2.3 Критерии типа χ2 при сложных гипотезах 2.4 Статистика типа χ2 Никулина 2.5 Связь мощности критериев со способом группирования наблюдений 2.6 Асимптотически оптимальное группирование 2.7 Характер влияния способов группирования и метода оценивания на распределения статистик типа χ2 2.8 Выбор числа интервалов 2.9 Рекомендации по использованию асимптотически оптимального группирования в критериях согласия 2.10 Примеры использования таблиц асимптотически оптимального группирования 3 Порядок применения критериев типа χ2 3.1 Порядок проверки простой гипотезы 3.2 Порядок проверки сложной гипотезы ПРИЛОЖЕНИЕ А Таблицы асимптотически оптимального группирования наблюдений в критериях согласия типа χ2 ПРИЛОЖЕНИЕ Б Процентные точки χ2 - распределений ПРИЛОЖЕНИЕ В Библиография
|
Предисловие
1 РАЗРАБОТАНЫ Новосибирским государственным техническим университетом, доработаны с участием Технического комитета по стандартизации ТК 125 «Стандартизация статистических методов управления качеством»
ВНЕСЕНЫ Техническим комитетом по стандартизации ТК 125 «Стандартизация статистических методов управления качеством»
2 ПРИНЯТЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Госстандарта России от 14 декабря 2001г. №525-ст
3 ВВЕДЕНЫ ВПЕРВЫЕ
4 ПЕРЕИЗДАНИЕ. Октябрь 2006 г.
Введение
Необходимость разработки настоящих рекомендаций вызвана следующими причинами.
Во-первых, в нормативных документах по стандартизации, устанавливающих правила проверки опытного распределения с теоретическим, нечетко определены правила применения критериев согласия типа χ2 при проверке сложных гипотез. Некорректное использование оценок параметров по точечным (негруппированным) наблюдениям зачастую приводит к неоправданному отклонению проверяемой гипотезы.
Во-вторых, способы группирования наблюдений (способы разбиения области определения случайной величины на интервалы) при применении критериев типа χ2 и выбор числа интервалов группирования не учитывают асимптотических свойств этих критериев. Неоднозначность процедуры группирования, неоптимальный выбор числа интервалов отражаются на мощности применяемого критерия, его способности различать близкие гипотезы, что, как правило, приводит к неоправданному принятию проверяемой гипотезы.
Настоящие рекомендации, с одной стороны, облегчают практическое применение критериев согласия типа χ2, обеспечивают корректность статистических выводов, с другой стороны, содержат новые сведения из рассматриваемого раздела математической статистики.
1 Область применения
Настоящие рекомендации содержат правила проверки согласия опытного распределения с теоретическим законом распределения непрерывной случайной величины и могут быть применены при разработке правил и рекомендаций по стандартизации, метрологии, распространяющихся на методы статистического анализа.
Настоящие рекомендации могут быть также использованы в качестве практического руководства по применению критериев согласия типа χ2 при статистической обработке результатов наблюдений, измерений, контроля и испытаний продукции.
2 Теоретические основы рекомендаций
2.1 Общие положения
Число моделей непрерывных законов распределений, используемых в задачах статистического анализа (при контроле качества, исследованиях надежности и т. д.), немногим превышает 100, а для описания наблюдаемых случайных величин в прикладных исследованиях в основном применяют порядка 30 параметрических законов и семейств распределений.
Это не покрывает многообразия случайных величин, встречаемых на практике. Корректное применение критериев согласия часто приводит (и должно приводить) к отклонению гипотез о принадлежности выборки удобному и привычному закону распределения, например нормальному, так как законы реальных случайных величин, являющиеся следствием многочисленных причин, сложнее тех моделей, которые обычно используют для их описания. Следовательно и модели должны быть более сложными.
Целью первичной обработки экспериментальных наблюдений обычно является установление закона распределения, наиболее хорошо описывающего случайную величину, выборку которой наблюдают. Насколько хорошо наблюдаемая выборка описывается теоретическим законом, проверяют с использованием различных критериев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретическим является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию (чаще всего) или необоснованному отклонению проверяемой гипотезы.
Различают простые и сложные
гипотезы о согласии. Простая проверяемая гипотеза имеет вид: H 0 : f ( x , θ) = f ( x , θ0), где f (•) - функция плотности; θ0 -
известный скалярный или векторный параметр теоретического распределения, с
которым проверяют согласие. Сложная гипотеза имеет вид ![]() где Θ -
пространство параметров и оценку
где Θ -
пространство параметров и оценку ![]() скалярного или
векторного параметра вычисляют по той же самой выборке, по которой проверяют
гипотезу о согласии.
скалярного или
векторного параметра вычисляют по той же самой выборке, по которой проверяют
гипотезу о согласии.
Схема процедуры проверки
гипотезы следующая. В соответствии с применяемым критерием согласия вычисляют
значение S * статистики S как
некоторой функции от выборки и теоретического закона распределения с плотностью f ( x , θ0) [или ![]() при сложной
гипотезе]. Для используемых на практике критериев асимптотические (предельные)
распределения g ( s | H 0 ) соответствующих статистик при условии истинности гипотезы H 0 обычно известны. В общем случае для простых и сложных гипотез эти
распределения различаются. Далее в принятой практике статистического анализа обычно
полученное значение статистики S * сравнивают с критическим значением S α при
заданном уровне значимости α . Нулевую гипотезу отвергают, если S * > S α (рисунок 1).
Критическое значение S α , определяемое в случае
одномерной статистики из уравнения
при сложной
гипотезе]. Для используемых на практике критериев асимптотические (предельные)
распределения g ( s | H 0 ) соответствующих статистик при условии истинности гипотезы H 0 обычно известны. В общем случае для простых и сложных гипотез эти
распределения различаются. Далее в принятой практике статистического анализа обычно
полученное значение статистики S * сравнивают с критическим значением S α при
заданном уровне значимости α . Нулевую гипотезу отвергают, если S * > S α (рисунок 1).
Критическое значение S α , определяемое в случае
одномерной статистики из уравнения
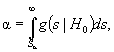
обычно берут из соответствующей статистической таблицы или вычисляют.
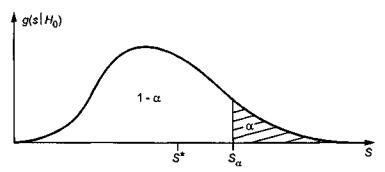
Рисунок 1 - Плотность распределения статистики при истинной гипотезе H0
Больше информации о степени
согласия можно почерпнуть из «достигаемого уровня значимости»: вероятности
возможного превышения полученного значения статистики при истинности нулевой
гипотезы 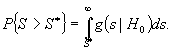 Именно эта
вероятность позволяет судить о том, насколько хорошо выборка согласуется с
теоретическим распределением, так как по существу представляет собой
вероятность истинности нулевой гипотезы (рисунок 2).
Гипотезу о согласии не отвергают, если P { S > S * } > α .
Именно эта
вероятность позволяет судить о том, насколько хорошо выборка согласуется с
теоретическим распределением, так как по существу представляет собой
вероятность истинности нулевой гипотезы (рисунок 2).
Гипотезу о согласии не отвергают, если P { S > S * } > α .
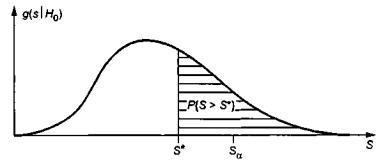
Рисунок 2 - Плотность распределения статистики при истинной гипотезе H0
Задачи оценивания параметров и проверки гипотез опираются на выборки независимых случайных величин. Случайность самой выборки предопределяет, что возможны и ошибки в результатах статистических выводов. С результатами проверки гипотез связывают ошибки двух видов, ошибка 1-го рода состоит в том, что отклоняют гипотезу H 0 , когда она верна; ошибка 2-го рода состоит в том, что принимают гипотезу H 0 , в то время как справедлива альтернативная (конкурирующая) гипотеза H 1 . Величина α задает вероятность ошибки 1-го рода. Обычно в критериях согласия не рассматривают конкретную альтернативу, и тогда конкурирующая гипотеза имеет вид H 1 : f ( x , θ) ≠ f ( x , θ0). Если гипотеза H 1 задана и имеет, например, вид H 1 : f ( x , θ) = f 1 ( x , θ1), то выбор значения α определяет для используемого критерия проверки гипотез и вероятность ошибки 2-го рода β. На рисунке 3 g ( s | H 0 ) отображает плотность распределения статистики S при истинности гипотезы H 0 , a g ( s | H 1 ) - плотность распределения статистики S при справедливости гипотезы H 1 .
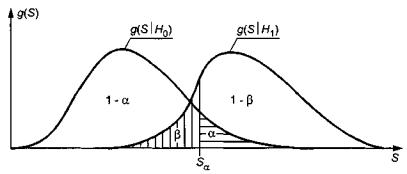
Рисунок 3 - Плотности распределения статистик при справедливости гипотез H0 и H1
Мощность критерия представляет собой значение 1 - β, где β - вероятность ошибки 2-го рода. Очевидно, что чем выше мощность используемого критерия при заданном значении α , тем лучше он различает гипотезы H 0 и H 1 . Особенно важно, чтобы используемый критерий хорошо различал близкие альтернативы. Графически требование максимальной мощности критерия означает, что на рисунке 3 плотности g ( s | H 0 ) и g ( s | H 1 ) должны быть максимально «раздвинуты».
2.2 Критерии типа χ2 при простых гипотезах
Предполагают, что ζ 1 , ζ 2 , ... , ζ N - выборка значений наблюдаемой случайной величины объема N . Процедура проверки гипотез с использованием критериев типа χ2 предусматривает группирование наблюдений. Область определения случайной величины разбивают на k непересекающихся интервалов граничными точками
х 0 < х 1 < ... < х k -1 < х k ,
где х0 - нижняя грань
области определения случайной величины; х k - верхняя грань. В соответствии с заданным разбиением подсчитывают число ni выборочных значений, попавших в i -й интервал, и вероятности попадания в
интервал 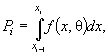 соответствующие
теоретическому закону с функцией плотности f (х, θ). При проверке простой
гипотезы известны как вид функции плотности, так и все параметры закона
(известен скалярный или векторный параметр θ). При этом
соответствующие
теоретическому закону с функцией плотности f (х, θ). При проверке простой
гипотезы известны как вид функции плотности, так и все параметры закона
(известен скалярный или векторный параметр θ). При этом ![]() В основе статистик,
используемых в критериях согласия χ2,
лежит измерение отклонений ni / N от Pi (θ).
В основе статистик,
используемых в критериях согласия χ2,
лежит измерение отклонений ni / N от Pi (θ).
К критериям такого рода, в частности, относят критерий χ2 Пирсона, критерий отношения правдоподобия [ 1] и критерии типа χ2 [ 2] - [ 5].
Статистику критерия согласия χ2 Пирсона S χ2 вычисляют по формуле
![]() ( 1)
( 1)
В случае проверки простой гипотезы в пределе
при N → ∞ эта статистика подчиняется ![]() распределению с r = k - 1 степенями свободы, если верна нулевая
гипотеза. Плотность
распределению с r = k - 1 степенями свободы, если верна нулевая
гипотеза. Плотность ![]() - распределения g ( s ) описывается формулой
- распределения g ( s ) описывается формулой
![]() (2)
(2)
Если верна конкурирующая гипотеза H 1 и выборка соответствует распределению с плотностью f 1 ( x ,
θ1) и параметром θ1, то эта же статистика в
пределе подчиняется нецентральному ![]() - распределению с тем же числом
степеней свободы r = k - 1 и параметром нецентральности
- распределению с тем же числом
степеней свободы r = k - 1 и параметром нецентральности
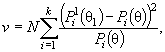 ( 3)
( 3)
где ![]() - вероятность
попадания в интервал при справедливой гипотезе H 1 . Плотность
нецентрального
- вероятность
попадания в интервал при справедливой гипотезе H 1 . Плотность
нецентрального ![]() - распределения g ( s , v ) имеет вид [ 1]
- распределения g ( s , v ) имеет вид [ 1]
![]() (4)
(4)
где В(α, β) = Г(α)Г(β)/Г(α + β) - бета-функция.
При заданном уровне значимости α нулевая гипотеза о согласии не должна быть отвергнута, если
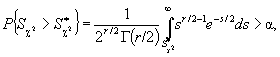 ( 5)
( 5)
где ![]() - вычисленное в
соответствии с формулой ( 1 ) значение статистики. Статистика критерия отношения правдоподобия S оп [ 1]
- вычисленное в
соответствии с формулой ( 1 ) значение статистики. Статистика критерия отношения правдоподобия S оп [ 1]
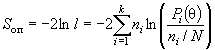 ( 6)
( 6)
при верной нулевой гипотезе также
асимптотически распределена как ![]() с r = k - 1 степенями свободы. Если верна конкурирующая
гипотеза H 1 и выборка соответствует распределению с
плотностью f 1 ( x , θ1) и параметром θ1 мерой близости
сравниваемых законов является величина
с r = k - 1 степенями свободы. Если верна конкурирующая
гипотеза H 1 и выборка соответствует распределению с
плотностью f 1 ( x , θ1) и параметром θ1 мерой близости
сравниваемых законов является величина
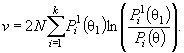 ( 7)
( 7)
2.3 Критерии типа χ2 при сложных гипотезах
При справедливости H 0 в случае проверки сложной гипотезы и при условии, что оценки
параметров найдены в результате минимизации статистики ![]() по этой же самой
выборке, статистика
по этой же самой
выборке, статистика ![]() асимптотически
распределена как
асимптотически
распределена как ![]() с числом степеней свободы r = k - m - 1, где m - число оцененных
параметров. Статистика
с числом степеней свободы r = k - m - 1, где m - число оцененных
параметров. Статистика ![]() имеет это же распределение, если в
качестве метода оценивания выбирают метод максимального правдоподобия и оценки
вычисляют по сгруппированным данным в результате максимизации по θ функции
правдоподобия
имеет это же распределение, если в
качестве метода оценивания выбирают метод максимального правдоподобия и оценки
вычисляют по сгруппированным данным в результате максимизации по θ функции
правдоподобия
![]() ( 8)
( 8)
где γ - некоторая константа и 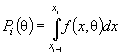 - вероятность попадания наблюдения в i -й интервал значений, зависящая от θ.
- вероятность попадания наблюдения в i -й интервал значений, зависящая от θ.
При вычислении оценок максимального
правдоподобия (ОМП) по негруппированным данным эта же статистика распределена
как сумма независимых слагаемых ![]() где ζ1, … , ζ m - стандартные нормальные случайные величины,
независимые одна от другой и от
где ζ1, … , ζ m - стандартные нормальные случайные величины,
независимые одна от другой и от ![]() а λ1, … , λ m - некоторые числа
между 0 и 1 [ 2],
[ 6],
[ 7],
представляющие собой корни уравнения
а λ1, … , λ m - некоторые числа
между 0 и 1 [ 2],
[ 6],
[ 7],
представляющие собой корни уравнения
|( l - λ) J (θ) - J Г (θ)| = 0.
В данном уравнении J (θ) - информационная матрица Фишера по негруппированным наблюдениям с элементами, определяемыми соотношением
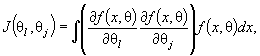 ( 9)
( 9)
a J Г (θ) - информационная матрица по группированным наблюдениям
![]() (10)
(10)
Функция распределения статистики
лежит между ![]() - и
- и ![]() - распределениями. В этом случае,
принимая нулевую гипотезу, следует удостовериться, что статистика
- распределениями. В этом случае,
принимая нулевую гипотезу, следует удостовериться, что статистика ![]() не превышает
критических значений
не превышает
критических значений ![]() и
и ![]() где α- задаваемый уровень значимости. И
если
где α- задаваемый уровень значимости. И
если ![]() <
< ![]() <
< ![]() , то,
принимая или отклоняя гипотезу о согласии, можно с одинаковым риском совершить
ошибку.
, то,
принимая или отклоняя гипотезу о согласии, можно с одинаковым риском совершить
ошибку.
Вышеизложенное относится и к критерию отношения правдоподобия.
Влияние способа группирования на распределения статистик при использовании оценок максимального правдоподобия по негруппированным данным - по 2.7.
2.4 Статистика типа χ2 Никулина
В работах [ 2]
- [ 5]
предложено видоизменение стандартной статистики ![]() , при котором предельное распределение есть обычное
, при котором предельное распределение есть обычное ![]() - распределение (число степеней
свободы не зависит от числа оцениваемых параметров). Неизвестные параметры
распределения F ( x , θ) в этом случае следует оценивать по негруппированным данным
методом максимального правдоподобия. При этом вектор Р = ( P 1 , … , Pk ) T предполагают
заданным, и граничные точки интервалов определяют по соотношениям х i (θ) = F - l ( P 1 + ... + Pi ),
- распределение (число степеней
свободы не зависит от числа оцениваемых параметров). Неизвестные параметры
распределения F ( x , θ) в этом случае следует оценивать по негруппированным данным
методом максимального правдоподобия. При этом вектор Р = ( P 1 , … , Pk ) T предполагают
заданным, и граничные точки интервалов определяют по соотношениям х i (θ) = F - l ( P 1 + ... + Pi ), ![]() Предложенная статистика имеет вид [ 3]
Предложенная статистика имеет вид [ 3]
![]() ( 11)
( 11)
где ![]() вычислена по формуле
( 1); матрица
вычислена по формуле
( 1); матрица 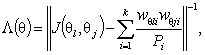 элементы и
размерность которой определяются оцениваемыми компонентами вектора параметров
θ; J (θ l , θ j ) - элементы информационной матрицы J (θ) по негруппированным данным ( 9); a θ l = w θ l 1 n 1 / P 1 + … + w θ lk nk / Pk - элементы
вектора а(θ) и
элементы и
размерность которой определяются оцениваемыми компонентами вектора параметров
θ; J (θ l , θ j ) - элементы информационной матрицы J (θ) по негруппированным данным ( 9); a θ l = w θ l 1 n 1 / P 1 + … + w θ lk nk / Pk - элементы
вектора а(θ) и
![]() (12)
(12)
Для распределений, которые полностью определяются только параметрами сдвига и масштаба, справедливо соотношение
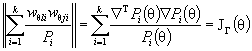 (13)
(13)
и, следовательно,
Λ(θ) = [ J (θ) - J Г (θ)]-1. ( 14)
Действительно, для законов с
параметрами сдвига θ1 и масштаба θ2 с функцией
распределения F (( x - θ1)/θ2) и плотностью ![]() элементы
информационной матрицы J Г (θ) имеют
вид:
элементы
информационной матрицы J Г (θ) имеют
вид:
![]()
![]()
![]()
где ti = ( xi - θ1)/θ2. Тогда
![]()
![]()
Если проверяемая гипотеза H 0 о принадлежности наблюдаемого закона параметрическому семейству f (х, θ) неверна и справедлива
конкурирующая гипотеза H 1 , которой соответствует распределение с
плотностью ![]() статистика
статистика ![]() в пределе подчиняется
нецентральному
в пределе подчиняется
нецентральному ![]() - распределению с параметром
нецентральности [ 3]
- распределению с параметром
нецентральности [ 3]
![]() ( 15)
( 15)
где 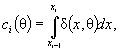 d θ l = w θ l 1 c 1 (θ)/ P 1 + … + w θ lk ck (θ)/ Pk - элементы вектора d (θ) , соответствующие оцениваемым компонентам вектора θ, а
размерность вектора равна числу оцениваемых параметров.
d θ l = w θ l 1 c 1 (θ)/ P 1 + … + w θ lk ck (θ)/ Pk - элементы вектора d (θ) , соответствующие оцениваемым компонентам вектора θ, а
размерность вектора равна числу оцениваемых параметров.
2.5 Связь мощности критериев со способом группирования наблюдений
Очевидно, что группирование наблюдений приводит к потере информации, и эти потери зависят от выбора способа группирования данных. Следуя рекомендациям различных литературных источников, на практике обычно строят интервалы равной длины или, в лучшем случае, интервалы равной вероятности. Потери информации о законе распределения в этих ситуациях различны, различна и способность критериев распознавать близкие гипотезы.
Мерой внутренней близости распределений случайных величин служит фишеровская информация, что связано с мощностью различения между близкими значениями параметра. Так как в любой статистике не больше информации, чем в исходной выборке, то мощность различения с помощью статистики не больше, чем с помощью всей выборки. Следовательно, если нужно выбирать между несколькими статистиками, следует предпочесть ту, для которой потери фишеровской информации минимальны [ 8].
Предполагают, что конкурирующей гипотезе Н 1 соответствует распределение того же типа, что и H 0 , но с параметром θ1. Можно показать, разлагая Pi (θ1) в соотношении ( 3) в ряд Тейлора при малых δθ = θ1 - θ и пренебрегая членами высшего порядка, что
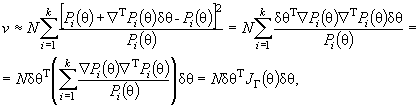 ( 16)
( 16)
где
![]()
- информационная матрица Фишера по группированным данным. Мощность критерия χ2 Пирсона представляет собой неубывающую функцию от v . Матрица потерь информации, вызванных группированием, ΔJ = J (θ) - J Г (θ), где J (θ) - информационная матрица Фишера по негруппированным наблюдениям, является неотрицательно определенной, и, следовательно, δθ T Δ J δθ ≥ 0. Так как δθ T J Г (θ)δθ = δθ T J (θ)δθ - δθ T ΔJ δθ, то очевидно, что с ростом потерь информации падает и мощность критерия при близких конкурирующих гипотезах.
Аналогично с ростом правой части соотношения ( 7) увеличивается мощность критерия отношения правдоподобия. Действуя как и в предыдущем случае и пренебрегая членами высшего порядка, можно будет иметь
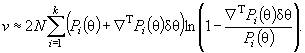
Далее, раскладывая ln (1 + х) по формуле Тейлора и вновь пренебрегая членами выше 2-го порядка, можно получить
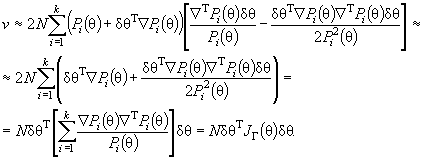 ( 17)
( 17)
Это соотношение аналогично соотношению ( 16).
Выражение ( 14) показывает, что свойства критерия, задаваемого статистикой ( 11), также зависят от потерь информации при группировании.
2.6 Асимптотически оптимальное группирование
На основании соотношений ( 16), ( 17) можно утверждать, что чем меньше потери информации, связанные с группированием наблюдений, тем выше мощность соответствующих критериев согласия при близких конкурирующих гипотезах.
Потери от группирования можно уменьшить, решая задачу асимптотически оптимального группирования и подбирая граничные точки так, чтобы J Г (θ) стремилась к информационной матрице по негруппированным данным J (θ). В случае скалярного параметра эта задача сводится к максимизации количества информации Фишера о параметре по группированной выборке
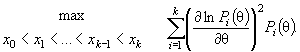 ( 18)
( 18)
А в случае вектора параметров в качестве критериев оптимальности могут быть выбраны различные функционалы от информационной матрицы Фишера. Наиболее естественно максимизировать определитель информационной матрицы, т. е. решать задачу
![]() ( 19)
( 19)
Применяя на практике критерии типа χ2, наиболее часто используют интервалы равной длины или, в лучшем случае, интервалы равной вероятности. Выбор равновероятного группирования обоснован определенностью этой процедуры разбиения и ее оптимальностью при отсутствии конкретных альтернатив [ 9]. Однако при использовании и равновероятного и равномерного группирования мощность как критерия χ2 Пирсона, так и критерия отношения правдоподобия обычно много ниже максимально возможной.
В общем случае информационная матрица Фишера зависит не только от граничных точек х i но и от параметров исследуемого распределения. Однако для достаточно широкого ряда распределений при решении задач асимптотически оптимального группирования граничные точки интервалов удается получить в виде, инвариантном относительно параметров распределений, и на их основе формировать таблицы асимптотически оптимального группирования.
Применение асимптотически оптимального группирования в критериях согласия типа χ2 впервые было предложено в работе [ 10]. Совокупность таблиц асимптотически оптимального группирования, построенная в результате решения задач ( 18) и ( 19) в [ 11] - [ 16] для распределений экспоненциального, полунормального, Рэлея, Максвелла, модуля многомерного нормального вектора, Парето, Эрланга, Лапласа, нормального, логарифмически нормальных ( ln и lg ), Коши, Вейбулла, распределений минимального и максимального значения, двойного показательного, гамма распределения, представлена в приложении А. Таблицы А.1 - А.58 могут быть использованы как при проверке гипотез, так и при оценивании. Полученные таблицы используют в программной системе [ 17] при проверке согласия по критериям χ2 Пирсона и отношения правдоподобия, а также при вычислении робастных оценок.
Для многих законов распределений граничные точки интервалов не могут быть выражены в виде, инвариантном относительно параметров распределений, т. е. они остаются функциями этих параметров. Это касается, например, таких законов, как гамма- и бета распределения [ 11], [ 15], экспоненциального семейства распределений. В этом случае формирование таблиц асимптотически оптимального группирования теряет смысл. Однако возможно решение задачи асимптотически оптимального группирования при конкретных значениях параметров в процессе проверки гипотез о согласии, как это реализуется в таких ситуациях в программной системе [ 17].
Положительный эффект применения асимптотически оптимального группирования на результатах статистического анализа проявляется при малых отклонениях выборки от предположений.
При проверке простых гипотез и использовании асимптотически оптимального группирования критерии χ2 Пирсона и отношения правдоподобия оказываются мощнее непараметрических критериев Колмогорова, Смирнова, ω2 и Ω 2 Мизеса против близких конкурирующих гипотез, лучше улавливают малые отклонения от предположений в наблюдаемых данных [ 18], [ 19].
2.7 Характер влияния способов группирования и метода оценивания на распределения статистик типа χ2
Вычисленные по конкретной выборке значения статистик типа χ2 очень сильно зависят от того, как сгруппированы данные. При выборе интервалов группирования одним способом нулевая гипотеза H 0 о согласии может быть отвергнута, другим - принята. При практическом использовании критериев согласия выбирают либо интервалы равной длины, либо интервалы равной вероятности (равной частоты), либо асимптотически оптимальные интервалы [ 10], [ 16] - [ 20]. Использование интервалов равной вероятности было предложено еще в работе [ 21]. Разбиение области определения случайной величины (размаха выборки) на интервалы равной длины неоднозначно. Более определенными способами являются равновероятное и асимптотически оптимальное группирования. При асимптотически оптимальном группировании мощность этих критериев для близких альтернатив максимальна [ 10], [ 18] - [ 20].
Для статистики χ2 Пирсона,
вычисляемой в соответствии с формулой ( 1 ), при справедливой простой гипотезе H 0 предельное распределение g ( S | H 0 ) есть ![]() - распределение с числом степеней
свободы r = k - 1. При сложной гипотезе, если по выборке оценивали m параметров закона, статистика подчиняется
- распределение с числом степеней
свободы r = k - 1. При сложной гипотезе, если по выборке оценивали m параметров закона, статистика подчиняется ![]() - распределению с r = k - m - 1 степеней свободы. При справедливой
альтернативной гипотезе H 1 предельное распределение g ( S | H 1 ) представляет собой нецентральное
- распределению с r = k - m - 1 степеней свободы. При справедливой
альтернативной гипотезе H 1 предельное распределение g ( S | H 1 ) представляет собой нецентральное ![]() - распределение с тем же числом
степеней свободы и параметром нецентральности, определяемым соотношением ( 3).
- распределение с тем же числом
степеней свободы и параметром нецентральности, определяемым соотношением ( 3).
В случае проверки сложных
гипотез и оценивании по выборке параметров распределений использование в
качестве предельных ![]() - распределений справедливо лишь при
определении оценок параметров по сгруппированным данным [ 1].
- распределений справедливо лишь при
определении оценок параметров по сгруппированным данным [ 1].
Все вышеизложенное относится и к критерию отношения правдоподобия, статистика которого определяется формулой ( 6).
Выбор способа группирования, в том числе равновероятного или асимптотически оптимального, отражается на предельных распределениях статистик g ( S | H 1 ) (при верной конкурирующей гипотезе). При использовании асимптотически оптимального группирования распределения g ( S | H 0 ) и g ( S | H 1 ) максимально «сдвинуты» относительно друг друга [ 18] - [ 20]. Это справедливо как при проверке простых, так и при проверке сложных гипотез.
В случае проверки простых
гипотез распределения g ( S | H 0 ) статистик критериев χ2 Пирсона и отношения правдоподобия при любом
разумном способе группирования [равновероятном (РВГ), асимптотически
оптимальном (АОГ), равной длины] хорошо согласуются с соответствующим ![]() - распределением [ 22],
[ 23].
- распределением [ 22],
[ 23].
При проверке сложных гипотез предельные распределения статистик критериев χ2 Пирсона и отношения правдоподобия могут зависеть не только от числа оцененных параметров, но и от способа группирования, вида наблюдаемого закона распределения f ( x , θ), метода оценивания и типа оцениваемого параметра.
В частности, при проверке сложных гипотез и использовании ОМП по негруппированным наблюдениям распределения g ( S | H 0 ) статистик данных критериев существенно зависят от способа группирования.
В работах [ 22], [ 23] методами статистического моделирования были проведены исследования законов распределения статистик типа χ2 при простых и различных сложных гипотезах, при справедливости гипотезы H 0 и справедливости конкурирующей гипотезы H 1 при равновероятном и асимптотически оптимальном группировании.
Например, на рисунках 4
- 7
сопоставлены полученные в результате моделирования эмпирические распределения
статистик (при вычислении ОМП по негруппированным наблюдениям) с
соответствующими ![]() - распределениями. Цифрой «1» на
указанных рисунках отмечено распределение статистики при асимптотически
оптимальном группировании, «2» - при равновероятном группировании. На рисунках 4
- 6
в качестве примера представлены распределения статистики
- распределениями. Цифрой «1» на
указанных рисунках отмечено распределение статистики при асимптотически
оптимальном группировании, «2» - при равновероятном группировании. На рисунках 4
- 6
в качестве примера представлены распределения статистики ![]() при справедливой
гипотезе H 0 для
пяти интервалов группирования и оценивании по негруппированным данным
параметров закона.
при справедливой
гипотезе H 0 для
пяти интервалов группирования и оценивании по негруппированным данным
параметров закона.
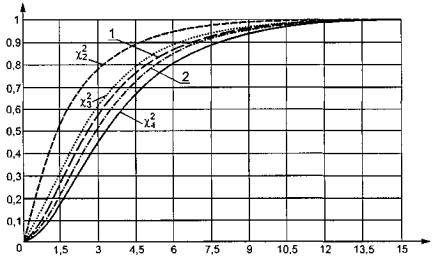
Рисунок 4 - Распределение статистики ![]() при пяти интервалах группирования и
оценивании масштабного параметра нормального распределения
при пяти интервалах группирования и
оценивании масштабного параметра нормального распределения
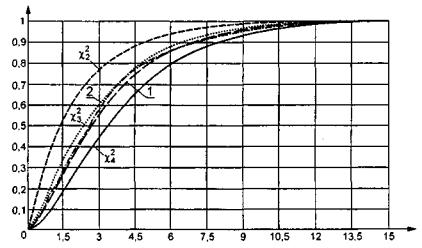
Рисунок 5 - Распределение статистики ![]() при пяти интервалах группирования и
оценивании параметра сдвига нормального распределения
при пяти интервалах группирования и
оценивании параметра сдвига нормального распределения
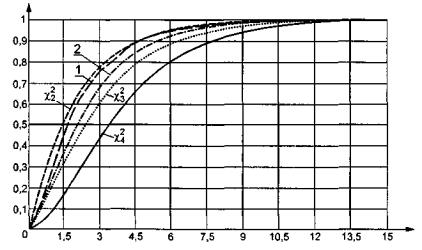
Рисунок 6 - Распределение статистики ![]() при пяти интервалах группирования и
оценивании двух параметров нормального распределения
при пяти интервалах группирования и
оценивании двух параметров нормального распределения
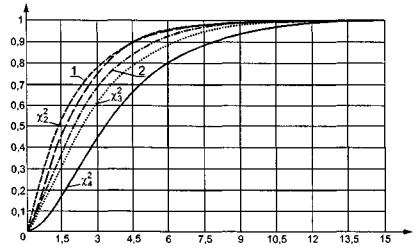
Рисунок 7 - Распределение статистики S оп при пяти интервалах группирования и оценивании двух параметров нормального распределения
Для сравнения на рисунке 7 представлены распределения статистики S оп при пяти интервалах группирования и оценивании обоих параметров нормального распределения при асимптотически оптимальном и равновероятном группировании.
Результаты моделирования и
анализа показали [ 22],
[ 23],
что распределения статистик критериев χ2
Пирсона и отношения правдоподобия при проверке сложных гипотез и вычислении
оценок по не группированным данным существенно различаются при разных способах
группирования. При этом эмпирический закон распределения статистики при
асимптотически оптимальном группировании ближе к ![]() - распределению, чем при
равновероятном группировании. Более того, распределения статистик зависят не
только от числа оцененных по выборке параметров, но и от того, какой параметр
оценивали. Например, оценивание параметра сдвига приводит к более значительному
изменению распределения статистики, чем оценивание масштабного параметра.
Распределения статистик зависят и от вида наблюдаемого закона. Но эта
зависимость не проявляется так резко, как в случае применения для проверки
сложных гипотез непараметрических критериев, например типа Колмогорова.
- распределению, чем при
равновероятном группировании. Более того, распределения статистик зависят не
только от числа оцененных по выборке параметров, но и от того, какой параметр
оценивали. Например, оценивание параметра сдвига приводит к более значительному
изменению распределения статистики, чем оценивание масштабного параметра.
Распределения статистик зависят и от вида наблюдаемого закона. Но эта
зависимость не проявляется так резко, как в случае применения для проверки
сложных гипотез непараметрических критериев, например типа Колмогорова.
Эмпирические распределения
статистики отношения правдоподобия оказываются ближе к ![]() - распределению, чем соответствующие
эмпирические распределения статистики χ2
Пирсона.
- распределению, чем соответствующие
эмпирические распределения статистики χ2
Пирсона.
![]() - распределение с числом степеней свободы r является
частным случаем гамма-распределения с основным параметром, равным r /2, и с масштабным - 0,5. Оценивание одного
из параметров учитывается уменьшением числа степеней свободы на 1. Так, если
измерять изменение предельного закона «в степенях свободы», то оказывается, что
оценивание по негруппированным наблюдениям даже параметра сдвига обычно приводит
к изменению «числа степеней» на значение, меньшее 1, еще к меньшему изменению в
степенях свободы приводит оценивание масштабного параметра. При оценивании по
негруппированным наблюдениям двух параметров закона различие между
- распределение с числом степеней свободы r является
частным случаем гамма-распределения с основным параметром, равным r /2, и с масштабным - 0,5. Оценивание одного
из параметров учитывается уменьшением числа степеней свободы на 1. Так, если
измерять изменение предельного закона «в степенях свободы», то оказывается, что
оценивание по негруппированным наблюдениям даже параметра сдвига обычно приводит
к изменению «числа степеней» на значение, меньшее 1, еще к меньшему изменению в
степенях свободы приводит оценивание масштабного параметра. При оценивании по
негруппированным наблюдениям двух параметров закона различие между ![]() -распределением и действительным
распределением статистики еще более значимо. Таким образом, при вычислении
оценок параметров по негруппированным наблюдениям использование в критериях
согласия
-распределением и действительным
распределением статистики еще более значимо. Таким образом, при вычислении
оценок параметров по негруппированным наблюдениям использование в критериях
согласия ![]() - распределения чревато занижением
вероятности вида P { S > S * } и определенным риском отвергнуть верную гипотезу H 0 . Занижение P { S > S * } более существенно при
малом числе интервалов группирования. В целом этот риск существенно меньше в
случае применения асимптотически оптимального группирования.
- распределения чревато занижением
вероятности вида P { S > S * } и определенным риском отвергнуть верную гипотезу H 0 . Занижение P { S > S * } более существенно при
малом числе интервалов группирования. В целом этот риск существенно меньше в
случае применения асимптотически оптимального группирования.
Полученные в результате моделирования эмпирические законы распределения статистик рассматриваемых критериев практически всегда с достаточно высокой точностью описываются гамма-распределением.
Использование в критериях
согласия ![]() - распределения для вычисления
вероятности вида P { S > S * } связано с риском
отвергнуть верную гипотезу H 0 . В случае применения асимптотически
оптимального группирования этот риск существенно меньше. В качестве примера в
таблице 1
приведены значения вероятностей P { S
> S * } для
различных значений статистики S , вычисленные по
- распределения для вычисления
вероятности вида P { S > S * } связано с риском
отвергнуть верную гипотезу H 0 . В случае применения асимптотически
оптимального группирования этот риск существенно меньше. В качестве примера в
таблице 1
приведены значения вероятностей P { S
> S * } для
различных значений статистики S , вычисленные по ![]() - распределению в соответствии с
«действительными» распределениями статистик при семи интервалах группирования и
оценивании двух параметров нормального распределения. Эти данные вместе с
другими результатами позволяют судить о том, что в случае применения
асимптотически оптимального группирования и использования
- распределению в соответствии с
«действительными» распределениями статистик при семи интервалах группирования и
оценивании двух параметров нормального распределения. Эти данные вместе с
другими результатами позволяют судить о том, что в случае применения
асимптотически оптимального группирования и использования ![]() - распределения ошибки при вычислении
вероятности P { S > S * } практически незначимы.
- распределения ошибки при вычислении
вероятности P { S > S * } практически незначимы.
Таблица 1 - Значения вероятностей вида P {S > S*}
|
Значение S * |
|
Распределение статистики S оп |
Распределение статистики |
||
|
При АОГ |
При РВГ |
При АОГ |
При РВГ |
||
|
3 |
0,5578 |
0,5876 |
0,6293 |
0,5914 |
0,6304 |
|
4 |
0,4060 |
0,4303 |
0,4700 |
0.4356 |
0,4716 |
|
5 |
0,2873 |
0,3049 |
0,3384 |
0,3108 |
0,3403 |
|
6 |
0,1991 |
0,2108 |
0,2370 |
0,2165 |
0,2389 |
|
7 |
0,1359 |
0,1430 |
0,1626 |
0,1481 |
0,1643 |
|
8 |
0,0916 |
0,0956 |
0,1096 |
0,0999 |
0,1111 |
|
9 |
0,0611 |
0,0632 |
0,0729 |
0,0666 |
0,0741 |
|
10 |
0,0404 |
0,0413 |
0,0480 |
0,0440 |
0,0489 |
|
11 |
0,0266 |
0,0268 |
0,0313 |
0,0288 |
0,0320 |
|
12 |
0,0173 |
0,0173 |
0,0202 |
0,0187 |
0,0207 |
|
13 |
0,0113 |
0,0110 |
0,0130 |
0,0120 |
0,0133 |
Исследование
распределений статистик при вычислении ОМП по негруппированным данным и
дальнейшем увеличении числа интервалов показало возрастающую близость
распределений статистик к ![]() - распределениям.
Следовательно, при использовании
- распределениям.
Следовательно, при использовании ![]() - распределения для вычисления
вероятностей вида P { S > S * } с ростом числа интервалов (при достаточном объеме выборки) ошибки
будут снижаться.
- распределения для вычисления
вероятностей вида P { S > S * } с ростом числа интервалов (при достаточном объеме выборки) ошибки
будут снижаться.
Как отражается способ
группирования на предельных распределениях статистики ![]() при справедливости альтернативной
гипотезы H 1 показано
на рисунках 8, 9, где
приведены полученные в результате моделирования функции распределения G ( S | H 1 ) при использовании асимптотически оптимального (АОГ) и равновероятного
(РВГ) группирования, когда гипотеза H 0 соответствует нормальному закону
распределения, а гипотеза H 1 - логистическому. Эти два закона достаточно близки и трудноразличимы с
помощью критериев согласия. На рисунке 8
приведены эмпирические распределения статистики при простой гипотезе H 0 , а на рисунке 9 - при
сложной. Число интервалов группирования - 7. Из рисунков 8, 9
видно, насколько выше мощность критерия при асимптотически оптимальном
группировании по сравнению равновероятным.
при справедливости альтернативной
гипотезы H 1 показано
на рисунках 8, 9, где
приведены полученные в результате моделирования функции распределения G ( S | H 1 ) при использовании асимптотически оптимального (АОГ) и равновероятного
(РВГ) группирования, когда гипотеза H 0 соответствует нормальному закону
распределения, а гипотеза H 1 - логистическому. Эти два закона достаточно близки и трудноразличимы с
помощью критериев согласия. На рисунке 8
приведены эмпирические распределения статистики при простой гипотезе H 0 , а на рисунке 9 - при
сложной. Число интервалов группирования - 7. Из рисунков 8, 9
видно, насколько выше мощность критерия при асимптотически оптимальном
группировании по сравнению равновероятным.
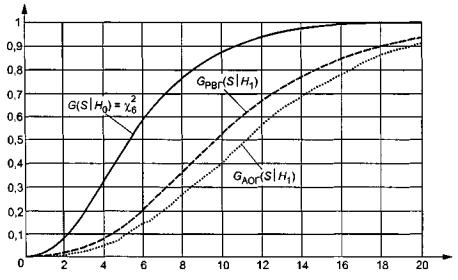
Рисунок 8 - Распределение статистики ![]() при проверке простой гипотезы H 0
при проверке простой гипотезы H 0
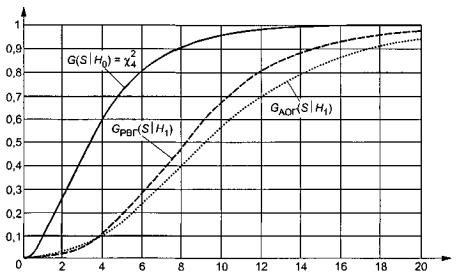
Рисунок 9 - Распределение статистики ![]() при проверке сложной
гипотезы H0
при проверке сложной
гипотезы H0
Распределения G ( S | H 0 ) и G ( S | H 1 ) статистики ![]() , определяемой
соотношением ( 11) при использовании
оценок максимального правдоподобия параметров по негруппированным данным,
несущественно зависят от способа группирования. Исследование этих распределений
методами статистического моделирования показало хорошее согласие G ( S | H 0 ) с
, определяемой
соотношением ( 11) при использовании
оценок максимального правдоподобия параметров по негруппированным данным,
несущественно зависят от способа группирования. Исследование этих распределений
методами статистического моделирования показало хорошее согласие G ( S | H 0 ) с ![]() -распределениями и при равновероятном
и при асимптотически оптимальном группировании. При выборе различных способов
группирования нет большой разницы между соответствующими распределениями
статистики G ( S | H 1 ). При этом критерий оказывается несколько
мощнее в случае равновероятного группирования.
-распределениями и при равновероятном
и при асимптотически оптимальном группировании. При выборе различных способов
группирования нет большой разницы между соответствующими распределениями
статистики G ( S | H 1 ). При этом критерий оказывается несколько
мощнее в случае равновероятного группирования.
Таким образом, по поводу распределений статистик критериев типа χ2 можно сделать следующие выводы.
Если по наблюдаемой выборке не
оценивали параметры закона (простая гипотеза), то распределения статистик типа χ2 при справедливой
гипотезе H 0 подчиняются ![]() - распределениям как при
равновероятном, так и при асимптотически оптимальном группировании. Различия
между распределениями статистик при равновероятном и асимптотически оптимальном
группировании заметны, но незначимы. Распределения статистик при равновероятном
группировании в целом оказываются ближе к
- распределениям как при
равновероятном, так и при асимптотически оптимальном группировании. Различия
между распределениями статистик при равновероятном и асимптотически оптимальном
группировании заметны, но незначимы. Распределения статистик при равновероятном
группировании в целом оказываются ближе к ![]() - распределению.
- распределению.
В условиях, когда оценки параметров определяют по негруппированным наблюдениям, распределения этих статистик хорошо описываются гамма-распределениями. При этом:
а) Распределения статистик критериев отношения правдоподобия и χ2 Пирсона существенно зависят от способа группирования, особенно при малом числе интервалов.
б) Распределения статистик зависят не только от числа оцененных по выборке параметров, но и от того, какой параметр оценивали. В частности, оценивание параметра сдвига приводит к более значительному изменению распределений статистик, чем оценивание масштабного параметра. Картина аналогична той, что наблюдается для распределений статистик типа Колмогорова, Смирнова и ω2 Мизеса при проверке сложных гипотез [ 24].
в) Эмпирические распределения
статистики отношения правдоподобия оказываются ближе к предельному теоретическому
![]() - распределению, чем соответствующие
эмпирические распределения статистики χ2
Пирсона.
- распределению, чем соответствующие
эмпирические распределения статистики χ2
Пирсона.
г) В целом, при малом числе
интервалов и оценивании m параметров число степеней свободы предельного
распределения уменьшается на «число степеней свободы», меньшее m . При этом эмпирический закон распределения статистики при асимптотически
оптимальном группировании ближе к теоретическому ![]() - распределению, чем при
равновероятном группировании.
- распределению, чем при
равновероятном группировании.
д) С ростом числа интервалов k разность между функцией распределения ![]() и действительными функциями
распределения статистик отношения правдоподобия и χ2 Пирсона в случае асимптотически оптимального
группирования убывает существенно быстрее.
и действительными функциями
распределения статистик отношения правдоподобия и χ2 Пирсона в случае асимптотически оптимального
группирования убывает существенно быстрее.
е) Анализ показал, что при
использовании для вычисления вероятностей P { S > S * } функции
распределения ![]() при асимптотически оптимальном
группировании и малом числе интервалов ( k < 10) при малых значениях P { S > S * } (именно при малых вероятностях принимают
решение отклонить гипотезу H 0 или нет) погрешность имеет значения, которые несущественны для
практических задач. То есть в этом случае, используя
при асимптотически оптимальном
группировании и малом числе интервалов ( k < 10) при малых значениях P { S > S * } (именно при малых вероятностях принимают
решение отклонить гипотезу H 0 или нет) погрешность имеет значения, которые несущественны для
практических задач. То есть в этом случае, используя ![]() - распределение, не совершают большой
ошибки. В то же время ошибка в определении критического значения S α может
быть достаточно большой. Поэтому целесообразно принимать решение по
достигнутому уровню значимости - значению вероятности P { S > S * } .
- распределение, не совершают большой
ошибки. В то же время ошибка в определении критического значения S α может
быть достаточно большой. Поэтому целесообразно принимать решение по
достигнутому уровню значимости - значению вероятности P { S > S * } .
ж) С ростом числа интервалов
(при соответствующем объеме выборки) отличие распределений статистик ![]() и S оп от распределений
и S оп от распределений ![]() и при асимптотически оптимальном и при
равновероятном группировании становится несущественным.
и при асимптотически оптимальном и при
равновероятном группировании становится несущественным.
При справедливости конкурирующей гипотезы H 1 распределения статистик χ2 и отношения правдоподобия при простых и сложных гипотезах сильно зависят от способа группирования.
Разность G ( S | H 0 ) - G ( S | H 1 ) для этих статистик при близких альтернативах в случае использования асимптотически оптимального группирования максимальна, следовательно, максимальна мощность критерия.
Распределения G ( S | H 1 ) статистики Никулина от выбранного способа группирования зависят несущественно.
2.8 Выбор числа интервалов
Число интервалов группирования, используемое при вычислении оценок параметров, построении гистограмм, вычислении статистик типа отношения правдоподобия или χ2 Пирсона, колеблется в очень широких пределах. Большинство рекомендуемых формул для оценки числа интервалов k носит эмпирический характер и обычно дает завышенные значения.
Определение числа интервалов связано с объемом выборки. Целый ряд рекомендаций из различных источников по выбору числа интервалов k дан в [ 25].
При выборе интервалов равной
длины определяющим является требование, чтобы число наблюдений, попавших в
интервалы, было не слишком малым и сравнимым. Такое требование выдвигают в
связи с опасением, что в противном случае распределение статистики типа χ2 не будет являться ![]() - распределением. При этом наиболее
часто рекомендуют, чтобы число наблюдений, попавших в интервал, было не менее
10. В [ 26]
отмечено, что на практике допустимо, чтобы число наблюдений в крайних
интервалах было менее пяти. В работах [ 21],
[ 27],
посвященных изучению мощности критерия χ2
Пирсона, в случае унимодального распределения допускается уменьшение
ожидаемых частот попадания наблюдений для одного или двух интервалов до 1 и
даже ниже. Статистическое моделирование подтверждает, что и в такой ситуации
распределения статистик типа χ2
хорошо согласуются с соответствующими
- распределением. При этом наиболее
часто рекомендуют, чтобы число наблюдений, попавших в интервал, было не менее
10. В [ 26]
отмечено, что на практике допустимо, чтобы число наблюдений в крайних
интервалах было менее пяти. В работах [ 21],
[ 27],
посвященных изучению мощности критерия χ2
Пирсона, в случае унимодального распределения допускается уменьшение
ожидаемых частот попадания наблюдений для одного или двух интервалов до 1 и
даже ниже. Статистическое моделирование подтверждает, что и в такой ситуации
распределения статистик типа χ2
хорошо согласуются с соответствующими ![]() - распределениями.
- распределениями.
Во многих источниках, например в [ 28], можно найти упоминание эвристической формулы Старджесса для определения «оптимального» числа интервалов
k = log2 N + 1 = 3,3lgN + 1.
В [ 29] для определения «оптимального» числа интервалов рекомендуют формулу Брукса и Каррузера
k = 5 lgN .
В [ 30] рекомендуют соотношение
![]()
В [ 27] для равновероятных интервалов их число устанавливают порядка
![]()
где t - квантиль стандартного нормального распределения для заданного уровня значимости. В ряде работ приводят модификации данной формулы. В [ 31] предлагают значение
k = 4 lgN ,
а в [ 32] - дальнейшее развитие этого соотношения
k = 5 lg N - 5.
В исследовании [ 33] получено соотношение
![]()
где κ - значение контрэксцесса ( ![]() μ4 - четвертый центральный момент случайной
величины; σ - стандартное отклонение).
μ4 - четвертый центральный момент случайной
величины; σ - стандартное отклонение).
При больших объемах выборок N разброс значений k , задаваемых различными формулами, достаточно велик. Поэтому на практике при выборе числа интервалов больше руководствуются тем, чтобы в интервалы попадало число наблюдений не менее 5 - 10. Так, например, в рекомендациях ВНИИМ им. Д. И. Менделеева [ 34] в зависимости от N предлагают следующие значения k :
|
N |
k |
|
40 - 100................................ |
7 - 9 |
|
100 - 500.............................. |
8 - 12 |
|
500 - 1000............................ |
10 - 16 |
|
1000 - 10000........................ |
12 - 22. |
Все вышеперечисленные
рекомендации опирались на предположение, что k следует
выбирать таким образом, чтобы вид гистограммы был как можно ближе к плавной
кривой плотности распределения генеральной совокупности. В [ 35]
показано, что уклонение гистограммы от плотности распределения в лучшем случае
имеет порядок ![]() достигаемый при числе
интервалов k порядка
достигаемый при числе
интервалов k порядка ![]() .
.
Очевидно, что «оптимальное» значение k зависит не только от объема выборки, но и от вида закона распределения и от способа группирования.
При асимптотически оптимальном группировании относительно скалярного параметра при 10, 11 интервалах в группированной выборке сохраняется около 98% информации, при оптимальном группировании относительно вектора параметров (два параметра) для 15 интервалов - около 95%. Дальнейшее увеличение числа интервалов существенного значения не имеет.
Конкретное число интервалов при асимптотически оптимальном группировании выбирают, исходя из следующих соображений. При оптимальном группировании вероятности попадания в интервалы в общем случае не равны. Обычно минимальны вероятности попадания в крайние интервалы. Поэтому k желательно выбирать из условия NPi ( θ ) ≥ 5 - 10 для любого интервала при оптимальном группировании. По крайней мере, минимальная ожидаемая частота должна быть больше 1. В случае использования равновероятного группирования порядок k должен быть примерно таким же, как и при асимптотически оптимальном группировании.
Большинство рекомендаций по выбору числа интервалов, в частности по выбору числа интервалов в случае асимптотически оптимального группирования, исходят из того, чтобы при данном N как можно лучше приблизить плотность распределения ее непараметрической оценкой (гистограммой). Исключение составляют рекомендации в [ 21], [ 27], где к выбору числа интервалов k подходят с позиций мощности критерия согласия.
Известно [ 36], [ 37], что при заданном объеме выборки, заданных конкурирующих гипотезах H 0 и H 1 выбранном способе группирования и фиксированном уровне значимости α с ростом числа интервалов к мощность критериев χ2 Пирсона и отношения правдоподобия падает. Очевидно, что выбор оптимального числа интервалов должен быть основан на необходимости построения критерия, обладающего наибольшей мощностью при близких конкурирующих гипотезах.
Об изменении мощности критерия χ2 Пирсона с ростом
числа интервалов при проверке простой гипотезы можно судить по рисунку 10.
Через ![]() обозначена статистика, вычисляемая в
соответствии с формулой ( 1 ). На рисунке 10
представлены полученные экспериментально распределения статистики
обозначена статистика, вычисляемая в
соответствии с формулой ( 1 ). На рисунке 10
представлены полученные экспериментально распределения статистики ![]() при числе интервалов k = 7; 10; 15; 20 и объеме выборки N = 500, когда гипотеза H 0 соответствует
нормальному закону, а H 1 - логистическому (два очень близких закона).
Для k = 7 на рисунке 10
приведены распределения при равновероятном
при числе интервалов k = 7; 10; 15; 20 и объеме выборки N = 500, когда гипотеза H 0 соответствует
нормальному закону, а H 1 - логистическому (два очень близких закона).
Для k = 7 на рисунке 10
приведены распределения при равновероятном ![]() и асимптотически оптимальном
и асимптотически оптимальном ![]() группировании. Ордината нижнего конца
соответствующей вертикальной черты определяет значение β (вероятность
ошибки 2-го рода) при уровне значимости α = 0,1 для соответствующего числа
интервалов. Мощность равна 1 - β. Как видно, в полном соответствии с
результатами работ [ 36],
[ 37]
при увеличении числа интервалов мощность критерия падает.
группировании. Ордината нижнего конца
соответствующей вертикальной черты определяет значение β (вероятность
ошибки 2-го рода) при уровне значимости α = 0,1 для соответствующего числа
интервалов. Мощность равна 1 - β. Как видно, в полном соответствии с
результатами работ [ 36],
[ 37]
при увеличении числа интервалов мощность критерия падает.
Примечание - ![]() - это распределение, соответствующее
- это распределение, соответствующее ![]()
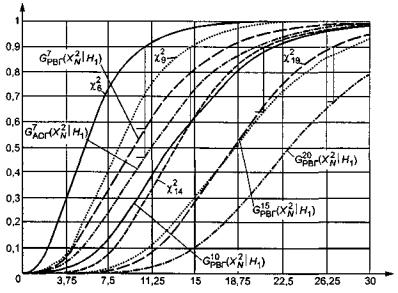
Рисунок
10 - Распределения статистики ![]() при проверке простой гипотезы ( H0 - нормальный закон, H1
- логистический закон, k = 7; 10; 15; 20)
при проверке простой гипотезы ( H0 - нормальный закон, H1
- логистический закон, k = 7; 10; 15; 20)
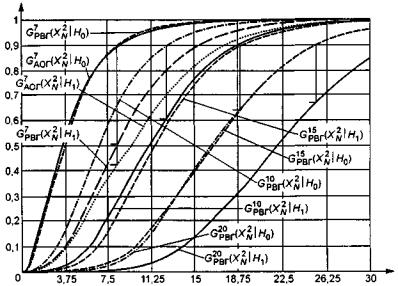
Рисунок
11 - Распределения статистики ![]() при проверке сложной гипотезы ( H0 - нормальный закон, H1 - логистический закон, k = 7; 10; 15; 20)
при проверке сложной гипотезы ( H0 - нормальный закон, H1 - логистический закон, k = 7; 10; 15; 20)
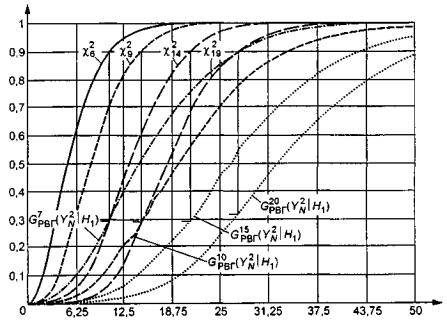
Рисунок
12 - Распределения статистики ![]() при проверке сложной гипотезы ( H0 - нормальный закон, H1
- логистический закон, k = 1; 10; 15; 20)
при проверке сложной гипотезы ( H0 - нормальный закон, H1
- логистический закон, k = 1; 10; 15; 20)
Аналогичные изменения мощности
критерия для статистики ![]() в зависимости от числа интервалов при
проверке сложной гипотезы иллюстрирует рисунок 11.
Здесь также с ростом k мощность критерия падает.
в зависимости от числа интервалов при
проверке сложной гипотезы иллюстрирует рисунок 11.
Здесь также с ростом k мощность критерия падает.
Мощность критерия Никулина с
использованием статистики ![]() с ростом k уменьшается
существенно медленней (рисунок 12),
и она выше, чем мощность критерия χ2
Пирсона.
с ростом k уменьшается
существенно медленней (рисунок 12),
и она выше, чем мощность критерия χ2
Пирсона.
Таблица 2 - Мощность критериев χ2 Пирсона и типа χ2 Никулина при уровне значимости α = 0,1 ( H0 - нормальный закон, H 1 - логистический закон)
|
k |
В случае простой гипотезы |
В случае сложной гипотезы |
||||
|
Для статистики |
Для статистики |
Для статистики |
||||
|
По результатам моделирования |
Теоретическая |
По результатам моделирования (при использовании ОМП) |
Теоретическая (при
использовании оценок min |
По результатам моделирования |
Теоретическая |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
6 |
0,46 |
0,449 |
0,53 |
0,526 |
0,70 |
0,739 |
|
7 |
0,43 |
0,427 |
0.49 |
0,488 |
0,71 |
0,750 |
|
8 |
0,42 |
0,409 |
0,45 |
0,459 |
0,71 |
0,755 |
|
9 |
0,38 |
0,395 |
0,43 |
0,436 |
0,71 |
0,756 |
|
10 |
0,38 |
0,383 |
0,43 |
0,418 |
0,71 |
0,756 |
|
11 |
0,37 |
0,373 |
0,41 |
0,403 |
0,71 |
0,754 |
|
12 |
0,35 |
0,364 |
0.41 |
0,391 |
0,70 |
0,752 |
|
13 |
0,35 |
0,357 |
0,38 |
0,381 |
0,70 |
0,749 |
|
14 |
0,34 |
0,351 |
0,38 |
0,373 |
0,69 |
0,746 |
|
15 |
0,33 |
0,345 |
0.38 |
0,365 |
0,69 |
0,742 |
|
16 |
0,33 |
0,340 |
0,38 |
0,359 |
0,69 |
0,738 |
|
17 |
0,32 |
0,336 |
0,37 |
0,353 |
0,69 |
0,734 |
|
18 |
0,32 |
0,332 |
0,37 |
0,348 |
0,69 |
0,730 |
|
19 |
0,32 |
0,328 |
0,35 |
0,343 |
0,68 |
0,726 |
|
20 |
0,31 |
0,325 |
0,35 |
0,339 |
0,68 |
0,722 |
|
21 |
0,31 |
0,322 |
0,34 |
0,335 |
0,67 |
0,718 |
|
22 |
0,31 |
0,319 |
0,34 |
0,331 |
0,67 |
0,714 |
|
23 |
0,31 |
0,317 |
0,34 |
0,328 |
0,66 |
0,710 |
|
24 |
0,30 |
0,314 |
0,34 |
0,325 |
0,66 |
0,707 |
|
25 |
0,30 |
0,312 |
0,34 |
0,322 |
0,66 |
0,703 |
|
26 |
0,30 |
0,310 |
0,33 |
0,320 |
0,65 |
0,699 |
|
27 |
0,30 |
0,308 |
0,33 |
0,317 |
0,65 |
0,695 |
|
28 |
0,30 |
0,306 |
0,32 |
0,315 |
0,65 |
0,692 |
|
29 |
0,30 |
0,304 |
0,32 |
0,313 |
0,65 |
0,688 |
|
30 |
0,30 |
0,302 |
0,32 |
0,310 |
0,65 |
0,684 |
В таблице 2
представлены значения мощности критериев χ2
Пирсона и типа χ2
Никулина при рассматриваемой паре альтернатив ( H 0 - нормальный
закон, H 1 - логистический закон)
при различном числе интервалов к в
случае простых и сложных гипотез. В колонке 2 приведены значения мощности
критерия χ2 Пирсона
при проверке простой гипотезы, полученные по результатам моделирования
(экспериментально). В колонке 3 приведены теоретические значения мощности,
вычисленные при условии, что ![]() представляет собой
представляет собой ![]() -распределение, a
-распределение, a ![]() - соответствующее нецентральное
распределение. Колонка 4 содержит значения мощности критерия χ2 Пирсона при
проверке сложной гипотезы, полученные по результатам моделирования при
использовании ОМП по негруппированным наблюдениям. В колонке 5 приведены
теоретические значения мощности критерия χ2
Пирсона при проверке сложной гипотезы, вычисленные при условии, что
- соответствующее нецентральное
распределение. Колонка 4 содержит значения мощности критерия χ2 Пирсона при
проверке сложной гипотезы, полученные по результатам моделирования при
использовании ОМП по негруппированным наблюдениям. В колонке 5 приведены
теоретические значения мощности критерия χ2
Пирсона при проверке сложной гипотезы, вычисленные при условии, что ![]() представляет собой
представляет собой ![]() - распределение (оценки параметров
вычисляют при минимизации статистики
- распределение (оценки параметров
вычисляют при минимизации статистики ![]() ) , a
) , a ![]() - соответствующее
нецентральное распределение. В колонке 6 приведены значения мощности критерия
Никулина, полученные в результате моделирования распределений статистики
- соответствующее
нецентральное распределение. В колонке 6 приведены значения мощности критерия
Никулина, полученные в результате моделирования распределений статистики ![]() , а в колонке 7 - расчетные значения мощности этой статистики
при рассматриваемой паре гипотез H 0 и H 1 .
, а в колонке 7 - расчетные значения мощности этой статистики
при рассматриваемой паре гипотез H 0 и H 1 .
В таблице 2
приведены значения мощности критериев для k от
6 до 30. Проследив изменение мощности критериев при k < 6, можно
убедиться, что, если мощность критерия χ2
Пирсона с уменьшением числа интервалов продолжает возрастать, то
мощность критерия Никулина со статистикой ![]() при k ≤ 6 начинает
падать. Это свидетельствует о том, что для критерия Никулина существует
оптимальное число интервалов, при котором его мощность максимальна.
при k ≤ 6 начинает
падать. Это свидетельствует о том, что для критерия Никулина существует
оптимальное число интервалов, при котором его мощность максимальна.
В [ 38] мощность критериев типа χ2 в зависимости от выбираемого числа интервалов к была исследована при различных проверяемых гипотезах H 0 и различных альтернативах H 1 при различных объемах выборок. Значение мощности для критериев типа χ2 может быть вычислено в соответствии с формулой [ 39]
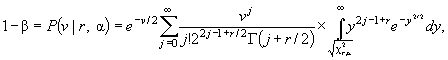 (20)
(20)
где v - параметр не центральности, определяемый
формулами ( 3), ( 7) или ( 15); ![]() - представляет собой
(1 - α)-процентную точку
- представляет собой
(1 - α)-процентную точку ![]() -распределения с r степенями свободы (α - заданная
вероятность ошибки 1-го рода, β -
вероятность ошибки 2-го рода). Максимальную мощность критерии χ2 Пирсона и
отношения правдоподобия зачастую имеют или при минимально возможном числе
интервалов, определяемом условием r = k - m - 1
≥ 1, или при оптимальном числе интервалов, близком к минимально
возможному. Оптимальное число интервалов для критерия Никулина обычно больше,
чем для критериев χ2 Пирсона
и отношения правдоподобия, и не превышает значения
-распределения с r степенями свободы (α - заданная
вероятность ошибки 1-го рода, β -
вероятность ошибки 2-го рода). Максимальную мощность критерии χ2 Пирсона и
отношения правдоподобия зачастую имеют или при минимально возможном числе
интервалов, определяемом условием r = k - m - 1
≥ 1, или при оптимальном числе интервалов, близком к минимально
возможному. Оптимальное число интервалов для критерия Никулина обычно больше,
чем для критериев χ2 Пирсона
и отношения правдоподобия, и не превышает значения ![]() .
.
Таким образом, выбирая число интервалов в критериях типа χ2, следует осознавать, что его увеличение не приводит к росту мощности критерия. Рекомендуется выбирать число интервалов k так, чтобы для любого интервала при оптимальном группировании выполнялось условие NPi (θ) ≥ 5 ¸ 10. По крайней мере, минимальная ожидаемая частота должна быть больше 1. При этом следует опираться на соответствующую таблицу асимптотически оптимального группирования из приложения А. Указания на соответствующую таблицу асимптотически оптимального группирования даны в таблице 3. Снизу значение k ограничено условием k ≥ m + 2.
Если заданы конкретная альтернатива и объем выборки N , можно выбрать оптимальное число k так, чтобы максимизировать соотношение ( 20).
2.9 Рекомендации по использованию асимптотически оптимального группирования в критериях согласия
Применяя критерии согласия типа χ2, можно по-разному разбивать область определения случайной величины на интервалы: равной длины, равных вероятностей или асимптотически оптимальные.
Использование асимптотически оптимальных интервалов обеспечивает максимальную мощность используемого критерия, снижает риск принятия неверной нулевой гипотезы H 0 .
Если гипотеза H 0 справедлива или, наоборот, совершенно не соответствует характеру выборки, то выводы по критериям согласия при равновероятном, равноотстоящем и асимптотически оптимальном группировании обычно оказываются очень близкими по вычисляемому значению вероятности P { S > S * } > α . Гипотезу H 0 при любом группировании однозначно принимают или однозначно отвергают.
В случае равновероятного и равноотстоящего группирования наличие в выборке малых отклонений от предположений (от гипотезы H 0 ) критерий не распознает. В случае асимптотически оптимального группирования эти отклонения будут заметны, что в принципе снижает риск принятия неверной нулевой гипотезы H 0 .
Применяя критерии согласия типа χ2, необязательно использовать только асимптотически оптимальное группирование наблюдений. Можно использовать и равновероятное группирование, и разбиение на интервалы равной длины. Но тогда следует помнить, что в этом случае критерии типа χ2 будут хуже различать близкие гипотезы (близкие альтернативы).
В приложении А приведены таблицы асимптотически оптимального группирования (АОГ) для ряда распределений. Представлены таблицы двух видов. В таблицах 1-го вида содержатся граничные точки, инвариантные относительно параметров распределения, в таблицах 2-го вида - вероятности попадания в соответствующие интервалы.
Порядок использования асимптотически оптимального группирования в связи с конкретным законом распределения определяется таблицей 3. В ней отражены функция плотности закона распределения, количество информации Фишера о соответствующем параметре по группированным и негруппированным данным, указаны номера таблиц в приложении А, в которых содержатся оптимальные для данной ситуации граничные точки в виде ti = φ( xi , θ), инвариантном относительно 9, и соответствующие значения вероятностей Pi попадания наблюдений в i -й интервал.
Для тех законов распределения, для которых решение задачи асимптотически оптимального группирования нельзя получить в виде, инвариантном относительно параметров распределений, например для распределений типа Накагами, бета-, и таблицы асимптотически оптимального группирования отсутствуют, в соответствующих колонках таблицы 3 стоят прочерки (тире). В таких случаях для того, чтобы применить асимптотически оптимальное группирование, можно рекомендовать решение задач асимптотически оптимального группирования вида ( 18), ( 19) в процессе проверки согласия при определенных значениях параметров, используя содержащиеся в таблице 3 выражения для элементов информационной матрицы Фишера по группированным данным.
Таблица 3 - Функции плотности распределений, элементы информационных матриц Фишера по группированным и негруппированным наблюдениям, соответствующие таблицы асимптотически оптимального группирования
|
Функция плотности распределения |
Параметр распределения |
Количество информации Фишера для параметра по наблюдениям |
Номер таблицы АОГ |
|||
|
группированным |
негруппированным |
ti |
Pi |
|||
|
1 |
Экспоненциальное |
θ0 |
|
|
А.1 |
А.2 |
|
2 |
Полунормальное |
θ0 |
|
|
А.6 |
А.7 |
|
3 |
Рэлея |
θ0 |
|
|
А.3 |
А.2 |
|
4 |
Максвелла |
θ0 |
|
|
А.4 |
А.5 |
|
5 |
Модуля нормального вектора |
θ0 |
при четном m при нечетном - |
|
|
|
|
m = 4 |
А.8 |
А.9 |
||||
|
m = 5 |
А.10 |
А.11 |
||||
|
m = 6 |
А.12 |
А.13 |
||||
|
m = 7 |
А.14 |
А.15 |
||||
|
m = 8 |
А.16 |
А.17 |
||||
|
m = 9 |
А.18 |
А.19 |
||||
|
6 |
Парето |
θ0 |
|
|
А.1 |
А.2 |
|
7 |
Эрланга порядка m |
θ 1 |
|
|
А.54 |
- |
|
8 |
Лапласа |
θ 0 |
|
|
А.46 А.47 |
А.48 А.49 |
|
9 |
Нормальное |
θ 0 |
|
|
А.24 |
А.25 |
|
θ 1 |
|
|
А.26 |
А.27 |
||
|
θ 0 , θ 1 |
|
0 |
А.28 |
А.29 |
||
|
10 |
Логарифмически ( ln ) |
θ 0 |
|
|
А.24 |
А.25 |
|
θ 1 |
|
|
А.26 |
А.27 |
||
|
θ 0 , θ 1 |
|
0 |
А.28 |
А.29 |
||
|
11 |
Логарифмически ( lg ) |
θ 0 |
|
|
А.24 |
А.25 |
|
θ 1 |
|
|
А.26 |
А.27 |
||
|
θ 0 , θ 1 |
|
0 |
А.28 |
А.29 |
||
|
12 |
Коши |
θ 0 |
|
|
А.36 |
А.37 |
|
θ 1 |
|
|
А.38 |
А.39 |
||
|
θ 0 , θ 1 |
|
0 |
А.40 |
|
||
|
13 |
Логическое |
θ 0 |
|
|
А.41 |
|
|
θ 1 |
|
|
А.42 |
А.43 |
||
|
θ 0 , θ 1 |
|
0 |
А.44 |
А.45 |
||
|
14 |
Вейбула C = 0.577215664 - постоянная Эйлера |
θ 0 |
|
|
А.20 |
А.21 |
|
θ 1 |
|
|
А.1 |
А.2 |
||
|
θ 0 , θ 1 |
|
|
А.22 |
А.23 |
||
|
15 |
Минимального значения |
θ 0 |
|
|
А.1 |
А.2 |
|
θ 1 |
|
|
А.20 |
А.21 |
||
|
θ 0 , θ 1 |
|
|
А.22 |
А.23 |
||
|
16 |
Максимального значения |
θ 0 |
|
|
А.30 |
А.31 |
|
θ 1 |
|
|
А.32 |
А.33 |
||
|
θ 0 , θ 1 |
|
|
А.34 |
А.35 |
||
|
17 |
Двойное показательное |
θ 0 |
|
|
А.50 |
А.51 |
|
θ 1 |
|
|
А.1 |
А.31 |
||
|
θ 0 , θ 1 |
|
|
А.52 |
А.35 |
||
|
18 |
Накагами |
θ 0 |
|
|
- |
- |
|
θ 1 |
|
|
- |
- |
||
|
θ 0 , θ 1 |
|
0 |
- |
- |
||
|
19 |
Гамма-распределение |
θ 0 |
|
|
А.53 |
А.54 |
|
θ 1 |
|
|
А.55 |
А.56 |
||
|
θ 0 , θ 1 |
|
|
А.57 |
А.58 |
||
|
20 |
Бета-распределение 1-го рода |
θ 0 |
|
|
- |
- |
|
θ 1 |
|
|
- |
- |
||
|
θ 0 , θ 1 |
|
|
- |
- |
||
|
21 |
Стандартное бета-распределение 2-го рода |
θ 0 |
См. соответствующие соотношения для бета - распределения 1-го рода |
|||
|
θ 1 |
См. соответствующие соотношения для бета - распределения 1-го рода |
|||||
|
θ 0 , θ 1 |
См. соответствующие соотношения для бета - распределения 1-го рода |
|||||
|
22 |
Бета-распределение 2-го рода |
θ 0 |
См. соответствующие соотношения для бета - распределения 1-го рода |
|||
|
θ 1 |
См. соответствующие соотношения для бета - распределения 1-го рода |
|||||
|
θ 0 , θ 1 |
См. соответствующие соотношения для бета - распределения 1-го рода |
|||||
|
θ 2 |
|
|
- |
- |
||
|
θ 0 , θ 2 |
|
|
- |
- |
||
|
θ 1 , θ 2 |
|
|
- |
- |
||
|
23 |
Распределение Sb -Джонса |
θ 0 |
|
1 |
А.24 |
А.25 |
|
θ 1 |
|
|
А.26 |
А.27 |
||
|
θ 0 , θ 1 |
|
|
А.28 |
А.29 |
||
|
24 |
Распределение Sl -Джонса |
θ 0 |
|
1 |
А.24 |
А.25 |
|
θ 1 |
|
|
А.26 |
А.27 |
||
|
θ 0 , θ 1 |
|
|
А.28 |
А.29 |
||
|
θ 2 |
|
|
А.24 |
А.25 |
||
|
θ 0 , θ 2 |
|
|
- |
- |
||
|
θ 1 , θ 2 |
|
|
- |
- |
||
|
25 |
Распределение Su -Джонса |
θ 0 |
|
1 |
А.24 |
А.25 |
|
θ 1 |
|
|
- |
- |
||
|
θ 0 , θ 1 |
|
|
А.28 |
А.29 |
||
|
θ 2 |
|
|
- |
- |
||
|
θ 0 , θ 2 |
|
|
- |
- |
||
|
θ 1 , θ 2 |
|
|
- |
- |
||
|
θ 3 |
|
|
- |
- |
||
|
θ 0 , θ 3 |
|
|
- |
- |
||
|
θ 1 , θ 3 |
|
|
- |
- |
||
|
θ 2 , θ 3 |
|
|
- |
- |
||
|
26 |
Класс экспоненциальных распределений |
θ 0 |
|
|
- |
- |
|
θ 1 |
|
|
- |
- |
||
|
θ 0 , θ 1 |
|
0 |
- |
- |
||
|
θ 2 |
|
0 |
- |
- |
||
|
θ 0 , θ 2 |
|
0 |
- |
- |
||
|
θ 1 , θ 2 |
|
|
- |
- |
||
Для законов распределения, определяемых одним параметром (экспоненциального, Парето, Рэлея и т. п.), одну и ту же пару таблиц асимптотически оптимального группирования ( ti и Pi ) используют при проверке простых и сложных гипотез.
Для законов распределения, определяемых двумя параметрами, в случае сложной гипотезы и оценивания только одного параметра требуемая пара таблиц асимптотически оптимального группирования указана в строке для этого параметра. В случае сложной гипотезы и оценивания двух параметров или в случае простой гипотезы используют пару таблиц, указанных в строке с двумя параметрами. В колонках для количества информации Фишера по группированным и негруппированным данным в такой строке даны выражения для недиагональных элементов соответствующих информационных матриц J (θ i , θ j ), а J (θ i , θ j ) = J (θ j , θ i ) .
Например, при оценивании по выборке только параметра сдвига нормального закона следует использовать пару таблиц А.24 - А.25, при оценивании только параметра масштаба - пару таблиц А.26 - А.27, а при проверке простых гипотез и сложных гипотез, сопровождаемых оцениванием по данной выборке обоих параметров нормального закона, - пару таблиц А.28 - А.29.
2.10 Примеры использования таблиц асимптотически оптимального группирования
Ниже на примерах рассмотрено применение асимптотически оптимального группирования в случае простых и сложных гипотез.
Пример 1 Проверяют простую гипотезу о принадлежности выборки экспоненциальному закону распределения. Упорядоченная выборка объемом 200 наблюдений имеет вид:
|
0,0005 |
0,0095 |
0,0189 |
0,0200 |
0,0225 |
0,0261 |
0,0339 |
0,0343 |
0,0463 |
0,0509 |
|
0,0625 |
0,0748 |
0,0797 |
0,0802 |
0,0857 |
0,0887 |
0,1049 |
0,1065 |
0,1276 |
0,1395 |
|
0,1465 |
0,1539 |
0,1565 |
0,1582 |
0,1584 |
0,1648 |
0,1679 |
0,1681 |
0,1689 |
0,1818 |
|
0,1940 |
0,1944 |
0,1950 |
0,1976 |
0,1992 |
0,2064 |
0,2260 |
0,2277 |
0,2311 |
0,2433 |
|
0,2441 |
0,2442 |
0,2509 |
0,2522 |
0,2566 |
0,2683 |
0,2840 |
0,3006 |
0,3025 |
0,3052 |
|
0,3056 |
0,3098 |
0,3158 |
0,3286 |
0,3288 |
0,3297 |
0,3396 |
0,3490 |
0,3578 |
0,3650 |
|
0,3728 |
0,3755 |
0,3823 |
0,3834 |
0,4017 |
0,4093 |
0,4135 |
0,4259 |
0,4419 |
0,4486 |
|
0,4487 |
0,4503 |
0,4587 |
0,4699 |
0,4711 |
0,4802 |
0,4814 |
0,4818 |
0,4981 |
0,4984 |
|
0,4989 |
0,5005 |
0,5085 |
0,5191 |
0,5279 |
0,5301 |
0,5328 |
0,5331 |
0,5389 |
0,5392 |
|
0,5432 |
0,5455 |
0,5548 |
0,5801 |
0,6001 |
0,6009 |
0,6694 |
0,6803 |
0,6817 |
0,6838 |
|
0,6844 |
0,6995 |
0,7127 |
0,7358 |
0,7515 |
0,7566 |
0,7699 |
0,7953 |
0,8048 |
0,8072 |
|
0,8116 |
0,8232 |
0,8271 |
0,8323 |
0,8771 |
0,8908 |
0,8949 |
0,9272 |
0,9571 |
0,9593 |
|
0,9682 |
0,9708 |
0,9761 |
0,9881 |
0,9931 |
1,0110 |
1,0188 |
1,0364 |
1,0447 |
1,0612 |
|
1,0683 |
1,0909 |
1,0984 |
1,1030 |
1,1068 |
1,1076 |
1,1100 |
1,1493 |
1,1562 |
1,1634 |
|
1,1702 |
1,1866 |
1,1964 |
1,2006 |
1,2103 |
1,2325 |
1,2607 |
1,2945 |
1,3185 |
1,3437 |
|
1,3918 |
1,4287 |
1,4398 |
1,4505 |
1,5068 |
1,5126 |
1,5491 |
1,5501 |
1,5681 |
1,5933 |
|
1,6323 |
1,6446 |
1,6686 |
1,6782 |
1,6816 |
1,6839 |
1,7054 |
1,7335 |
1,7560 |
1,7629 |
|
1,7677 |
1,7681 |
1,9750 |
1,9840 |
1,9873 |
2,0031 |
2,0870 |
2,0877 |
2,0957 |
2,1226 |
|
2,1382 |
2,1925 |
2,1950 |
2,2029 |
2,2315 |
2,2318 |
2,3487 |
2,4474 |
2,5498 |
2,8392 |
|
2,9899 |
3,0846 |
3,1179 |
3,3316 |
3,5926 |
3,5937 |
3,6218 |
4,0604 |
4,8403 |
6,0534 |
Проверяемая гипотеза
имеет вид ![]() при θ 0 = 1, θ 1 = 0. Оптимальные граничные
точки в виде ti = θ 0(х i - θ1) берут из таблицы А.1.
Выбирают число интервалов k = 5, так как Р k Ч n = 0,0 189Ч200 > 3, а при большем числе интервалов ожидаемые частоты
попадания в крайний интервал будут еще меньше. При k = 5 значения ti соответственно: 0,6004; 1,3545; 2,3720;
3,9657. При θ 0
= 1, θ 1 = 0
значения xi совпадают со значениями ti Соответствующие такому разбиению вероятности
попадания наблюдений в интервал берут из таблицы А.2:
0,4514; 0,2905; 0,1648; 0,0744; 0,0189. По выборке находят числа наблюдений ni , попавших в соответствующие интервалы (95,
55, 37, 10, 3). В соответствии с формулой ( 1)
вычисляют значение статистики
при θ 0 = 1, θ 1 = 0. Оптимальные граничные
точки в виде ti = θ 0(х i - θ1) берут из таблицы А.1.
Выбирают число интервалов k = 5, так как Р k Ч n = 0,0 189Ч200 > 3, а при большем числе интервалов ожидаемые частоты
попадания в крайний интервал будут еще меньше. При k = 5 значения ti соответственно: 0,6004; 1,3545; 2,3720;
3,9657. При θ 0
= 1, θ 1 = 0
значения xi совпадают со значениями ti Соответствующие такому разбиению вероятности
попадания наблюдений в интервал берут из таблицы А.2:
0,4514; 0,2905; 0,1648; 0,0744; 0,0189. По выборке находят числа наблюдений ni , попавших в соответствующие интервалы (95,
55, 37, 10, 3). В соответствии с формулой ( 1)
вычисляют значение статистики ![]() . При справедливости H 0 статистика подчиняется
. При справедливости H 0 статистика подчиняется ![]() - распределению и при значениях уровня
значимости
- распределению и при значениях уровня
значимости 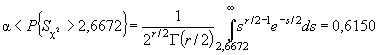 гипотеза H 0 будет принята.
Вычисляемое в соответствии с соотношением ( 3 ) значение статистики отношения правдоподобия
S оп = 2,8694; P { S оп > 2,8694} = 0,5799. Таким образом, в
соответствии сданным критерием также нет оснований для отклонения гипотезы H 0 . На рисунке 13
представлены плотность, гистограмма и результаты проверки согласия.
гипотеза H 0 будет принята.
Вычисляемое в соответствии с соотношением ( 3 ) значение статистики отношения правдоподобия
S оп = 2,8694; P { S оп > 2,8694} = 0,5799. Таким образом, в
соответствии сданным критерием также нет оснований для отклонения гипотезы H 0 . На рисунке 13
представлены плотность, гистограмма и результаты проверки согласия.
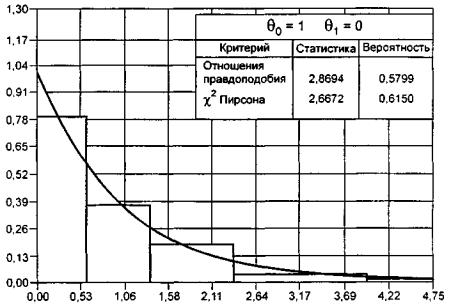
Рисунок 13 - Результаты проверки согласия к примеру 1
Пример 2 Проверяют сложную гипотезу о принадлежности выборки экспоненциальному закону распределения. Упорядоченная выборка объемом 300 наблюдений имеет вид:
|
0,0204 |
0,0242 |
0,0336 |
0,0342 |
0,0410 |
0,0511 |
0,0539 |
0,0859 |
0,0888 |
0,0925 |
|
0,0970 |
0,0996 |
0,1006 |
0,1039 |
0,1065 |
0,1067 |
01158 |
0,1170 |
0,1185 |
0,1188 |
|
0,1206 |
0,1207 |
0,1215 |
0,1260 |
0,1336 |
0,1336 |
0,1389 |
0,1462 |
0,1518 |
0,1565 |
|
0,1641 |
0,1664 |
0,1677 |
0,1738 |
0,1785 |
0,1812 |
0,1823 |
0,1889 |
0,2002 |
0,2032 |
|
0,2042 |
0,2074 |
0,2143 |
0,2221 |
0,2223 |
0,2265 |
0,2299 |
0,2335 |
0,2351 |
0,2408 |
|
0,2413 |
0,2424 |
0,2566 |
0,2576 |
0,2676 |
0,2697 |
0,2745 |
0,2749 |
0,2766 |
0,2780 |
|
0,2785 |
0,2826 |
0,2839 |
0,2909 |
0,2936 |
0,3029 |
0,3097 |
0,3251 |
0,3280 |
0,3352 |
|
0,3593 |
0,3597 |
0,3675 |
0,3688 |
0,3751 |
0,3816 |
0,3831 |
0,3875 |
0,3934 |
0,4049 |
|
0,4057 |
0,4057 |
0,4127 |
0,4133 |
0,4146 |
0,4212 |
0,4225 |
0,4231 |
0,4236 |
0,4363 |
|
0,4381 |
0,4414 |
0,4493 |
0,4553 |
0,4649 |
0,4712 |
0,4733 |
0,4798 |
0,4816 |
0,4817 |
|
0,4837 |
0,4880 |
0,4890 |
0,4917 |
0,4927 |
0,4982 |
0,5044 |
0,5081 |
0,5092 |
0,5135 |
|
0,5245 |
0,5301 |
0,5350 |
0,5351 |
0,5430 |
0,5432 |
0,5534 |
0,5609 |
0,5636 |
0,5637 |
|
0,5747 |
0,5806 |
0,5891 |
0,5898 |
0,5926 |
0,5962 |
0,6099 |
0,6137 |
0,6423 |
0,6670 |
|
0,6696 |
0,6713 |
0,6759 |
0,6885 |
0,6910 |
0,6913 |
0,6990 |
0,7043 |
0,7089 |
0,7150 |
|
0,7180 |
0,7189 |
0,7197 |
0,7226 |
0,7343 |
0,7530 |
0,7627 |
0,7635 |
0,7639 |
0,7822 |
|
0,7883 |
0,7889 |
0,7930 |
0,7943 |
0,7972 |
0,7979 |
0,8190 |
0,8191 |
0,8214 |
0,8234 |
|
0,8289 |
0,8291 |
0,8327 |
0,8382 |
0,8400 |
0,8408 |
0,8466 |
0,8571 |
0,8655 |
0,8679 |
|
0,8770 |
0,8895 |
0,8898 |
0,8925 |
0,8971 |
0,9041 |
0,9106 |
0,9134 |
0,9216 |
0,9234 |
|
0,9279 |
0,9395 |
0,9430 |
0,9458 |
0,9550 |
0,9625 |
0,9693 |
0,9792 |
0,9855 |
0,9877 |
|
1,0074 |
1,0127 |
1,0130 |
1,0172 |
1,0225 |
1,0227 |
1,0254 |
1,0520 |
1,0537 |
1,0720 |
|
1,0761 |
1,1009 |
1,1041 |
1,1071 |
1,1183 |
1,1586 |
1,1630 |
1,1719 |
1,1766 |
1,1909 |
|
1,1980 |
1,1986 |
1,2061 |
1,2169 |
1,2240 |
1,2298 |
1,2633 |
1,2698 |
1,2722 |
1,2749 |
|
1,2990 |
1,3150 |
1,3262 |
1,3345 |
1,3366 |
1,3369 |
1,3409 |
1,3423 |
1,3456 |
1,3501 |
|
1,3507 |
1,3518 |
1,3765 |
1,3791 |
1,3836 |
1,4011 |
1,4236 |
1,4339 |
1,4583 |
1,4630 |
|
1,4872 |
1,4935 |
1,5021 |
1,5291 |
1,5326 |
1,5347 |
1,5360 |
1,5503 |
1,5638 |
1,5642 |
|
1,5727 |
1,5934 |
1,6162 |
1,6165 |
1,6488 |
1,6543 |
1,6668 |
1,6916 |
1,7138 |
1,7300 |
|
1,7316 |
1,7339 |
1,7905 |
1,8173 |
1,8480 |
1,8725 |
1,8863 |
1,9178 |
1,9426 |
1,9720 |
|
1,9804 |
2,0209 |
2,0388 |
2,0816 |
2,1159 |
2,1169 |
2,1566 |
2,1732 |
2,1754 |
2,2319 |
|
2,2391 |
2,2620 |
2,3139 |
2,3222 |
2,3830 |
2,4445 |
2,4560 |
2,4864 |
2,5580 |
2,5796 |
|
2,7214 |
2,7843 |
3,0117 |
3,1078 |
3,1312 |
3,1805 |
3,2445 |
3,4491 |
3,6123 |
4,9320 |
Проверяемая гипотеза ![]() При этом θ 0 оценивают по выборке.
Оценка максимального правдоподобия
При этом θ 0 оценивают по выборке.
Оценка максимального правдоподобия ![]() Оптимальные граничные
точки в виде ti = θ 0(х i - θ1) как и в предыдущем случае берут из таблицы А.1 при k = 5: 0,6004; 1,3545;
2,3720; 3,9657. При θ 0 = 1,066851 и θ 1 = 0 вычисляют значения х i = ti / θ 0 + θ 1 : 0,5628; 1,2696; 2,2234; 3,7172. Вероятности попадания наблюдений в
интервал из таблицы А.2 : 0,4514; 0,2905; 0,1648; 0,0744; 0,0189. По
выборке находят числа наблюдений ni , попавших в соответствующие интервалы (118, 99, 62, 20, 1). В
соответствии с соотношением ( 1 ) вычисляют значение статистики
Оптимальные граничные
точки в виде ti = θ 0(х i - θ1) как и в предыдущем случае берут из таблицы А.1 при k = 5: 0,6004; 1,3545;
2,3720; 3,9657. При θ 0 = 1,066851 и θ 1 = 0 вычисляют значения х i = ti / θ 0 + θ 1 : 0,5628; 1,2696; 2,2234; 3,7172. Вероятности попадания наблюдений в
интервал из таблицы А.2 : 0,4514; 0,2905; 0,1648; 0,0744; 0,0189. По
выборке находят числа наблюдений ni , попавших в соответствующие интервалы (118, 99, 62, 20, 1). В
соответствии с соотношением ( 1 ) вычисляют значение статистики ![]()
При справедливости гипотезы H 0 статистика
подчиняется ![]() - распределению. Вероятность
- распределению. Вероятность
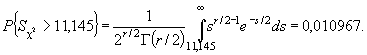
Уже при значениях α = 0,05 нет оснований для принятия гипотезы H 0 , но есть основание проверить и другие распределения. Результаты проверки гипотезы о согласии иллюстрирует рисунок 14.
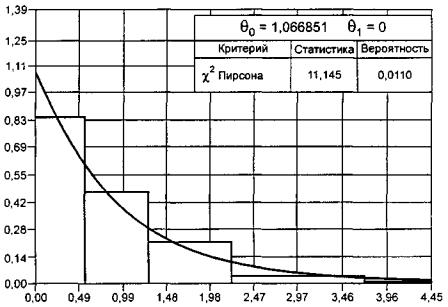
Рисунок 14 - Результаты проверки согласия к примеру 2
Пример 3 Проверяют простую гипотезу о принадлежности выборки нормальному закону распределения. Упорядоченная выборка объемом 300 наблюдений имеет вид:
|
- 5,1852 |
- 3,7318 |
- 3,2899 |
- 3,1038 |
- 2,9031 |
- 2,7243 |
- 2,7011 |
- 2,6448 |
- 2,5168 |
- 2,4975 |
|
- 2,4858 |
- 2,4268 |
- 2,1459 |
- 1,9894 |
- 1,9467 |
- 1,9348 |
- 1,9273 |
-1,8873 |
- 1,8383 |
- 1,8217 |
|
- 1,6802 |
- 1,6713 |
- 1,6704 |
- 1,6420 |
- 1,6322 |
- 1,6315 |
- 1,6005 |
- 1,5491 |
- 1,5238 |
- 1,5204 |
|
- 1,4727 |
- 1,4546 |
- 1,3420 |
- 1,3233 |
- 1,3225 |
- 1,3150 |
- 1,3097 |
- 1,2917 |
- 1,2767 |
- 1,2046 |
|
- 1,1606 |
- 1,1334 |
- 1,1259 |
- 1,0769 |
- 1,0659 |
- 1,0446 |
- 1,0258 |
- 1,0138 |
- 1,0077 |
- 0,9914 |
|
- 0,9818 |
- 0,9546 |
- 0,9511 |
- 0,9167 |
- 0,8927 |
- 0,8758 |
- 0,8311 |
- 0,8302 |
-0,8171 |
- 0,7794 |
|
- 0,7571 |
- 0,7228 |
- 0,7211 |
- 0,7064 |
- 0,6991 |
- 0,6873 |
- 0,6743 |
- 0,6442 |
- 0,6440 |
- 0,5798 |
|
- 0,5421 |
- 0,5308 |
- 0,5108 |
- 0,4845 |
-0,4491 |
- 0,4294 |
-0,4212 |
- 0,3943 |
-0,3251 |
- 0,2607 |
|
- 0,2506 |
-0,2351 |
- 0,2201 |
- 0,1698 |
- 0,1326 |
- 0,1217 |
- 0,0368 |
- 0,0194 |
0,0014 |
0,0108 |
|
0,0470 |
0,0728 |
0,0822 |
0,1281 |
0,1284 |
0,1455 |
0,1498 |
0,1539 |
0,1564 |
0,1895 |
|
0,1949 |
0,2079 |
0,2402 |
0,2643 |
0,2669 |
0,3104 |
0,3616 |
0,3723 |
0,4415 |
0,4929 |
|
0,5315 |
0,5318 |
0,5350 |
0,5359 |
0,5396 |
0,5843 |
0,5877 |
0,5944 |
0,6205 |
0,6279 |
|
0,6345 |
0,6391 |
0,6416 |
0,6445 |
0,6592 |
0,6630 |
0,6990 |
0,7361 |
0,7419 |
0,7426 |
|
0,7472 |
0,7511 |
0,7658 |
0,8359 |
0,8499 |
0,8681 |
0,9283 |
0,9368 |
0,9504 |
0,9657 |
|
0,9782 |
1,0158 |
1,0381 |
1,0505 |
1,0702 |
1,0873 |
1,0913 |
1,1313 |
1,1750 |
1,1908 |
|
1,2197 |
1,2347 |
1,2620 |
1,2799 |
1,3040 |
1,3160 |
1,3186 |
1,3245 |
1,3529 |
1,3729 |
|
1,3857 |
1,3979 |
1,4047 |
1,4101 |
1,4194 |
1,4485 |
1,4515 |
1,4782 |
1,4850 |
1,5759 |
|
1,6056 |
1,6076 |
1,6220 |
1,6223 |
1,6311 |
1,6395 |
1,6476 |
1,6610 |
1,6793 |
1,6800 |
|
1,6908 |
1,7208 |
1,7356 |
1,7358 |
1,7359 |
1,7550 |
1,8296 |
1,8573 |
1,8757 |
1,9448 |
|
1,9451 |
1,9924 |
2,0045 |
2,0153 |
2,0338 |
2,0400 |
2,0557 |
2,1055 |
2,1161 |
2,1224 |
|
2,1237 |
2,2229 |
2,2289 |
2,2432 |
2,2600 |
2,2989 |
2,3003 |
2,3088 |
2,3315 |
2,3659 |
|
2,4024 |
2,4152 |
2,4187 |
2,4600 |
2,4914 |
2,5100 |
2,5145 |
2,5311 |
2,5515 |
2,5706 |
|
2,5916 |
2,6982 |
2,7127 |
2,7282 |
2,7553 |
2,7778 |
2,8131 |
2,8296 |
2,8364 |
2,8445 |
|
2,8552 |
2,9012 |
2,9126 |
2,9517 |
3,0283 |
3,0510 |
3,1031 |
3,1199 |
3,1451 |
3,1453 |
|
3,1539 |
3,1633 |
3,2561 |
3,2995 |
3,3040 |
3,3056 |
3,3152 |
3,3159 |
3,3208 |
3,3567 |
|
3,4532 |
3,5665 |
3,5775 |
3,5782 |
3,5858 |
3,6054 |
3,6368 |
3,6435 |
3,6630 |
3,6788 |
|
3,6798 |
3,6985 |
3,6993 |
3,7203 |
3,7421 |
3,8047 |
3,8366 |
3,8389 |
3,9597 |
3,9682 |
|
3,9784 |
3,9828 |
3,9894 |
4,1512 |
4,1674 |
4,1887 |
4,2089 |
4,4316 |
4,4451 |
4,5262 |
|
4,5282 |
4,5397 |
4,5459 |
4,5898 |
4,6170 |
4,6560 |
4,6902 |
4,7263 |
4,7912 |
5,0490 |
|
5,1871 |
5,2678 |
5,4110 |
5,5609 |
5,6245 |
5,6484 |
5,6736 |
5,7743 |
6,1626 |
6,2185 |
Проверяемая гипотеза
имеет вид ![]() Оптимальные граничные
точки в виде ti = (х i - θ0)θ 1 берут из таблицы А.28 при k =
7(-2,0600; -1,2647; -0,4918; 0,4918; 1,2647; 2,0600), так как из таблицы А.29 P k Ч n = 0,0197Ч300 > 5. При θ0 = 1, θ 1 , =2 принимают значения: -3,12; -1,5294;
0,0164; 1,9836; 3,5294; 5,12. Вероятности попадания наблюдений в интервал из
таблицы А.29 : 0,0197; 0,0833; 0,2084; 0,3772; 0,2084;
0,0833; 0,0197. По выборке находят количества наблюдений ni попавших в соответствующие интервалы (3, 25,
62, 101, 60, 39, 10). В соответствии с соотношением ( 1 ) вычисляют значение статистики
Оптимальные граничные
точки в виде ti = (х i - θ0)θ 1 берут из таблицы А.28 при k =
7(-2,0600; -1,2647; -0,4918; 0,4918; 1,2647; 2,0600), так как из таблицы А.29 P k Ч n = 0,0197Ч300 > 5. При θ0 = 1, θ 1 , =2 принимают значения: -3,12; -1,5294;
0,0164; 1,9836; 3,5294; 5,12. Вероятности попадания наблюдений в интервал из
таблицы А.29 : 0,0197; 0,0833; 0,2084; 0,3772; 0,2084;
0,0833; 0,0197. По выборке находят количества наблюдений ni попавших в соответствующие интервалы (3, 25,
62, 101, 60, 39, 10). В соответствии с соотношением ( 1 ) вычисляют значение статистики ![]() При справедливости
гипотезы H 0 статистика подчиняется
При справедливости
гипотезы H 0 статистика подчиняется ![]() - распределению. Вероятность
- распределению. Вероятность ![]() При значениях уровня
значимости α > 0,0353 гипотеза H 0 будет отклонена. Результаты проверки
гипотезы о согласии показаны на рисунке 15.
При значениях уровня
значимости α > 0,0353 гипотеза H 0 будет отклонена. Результаты проверки
гипотезы о согласии показаны на рисунке 15.
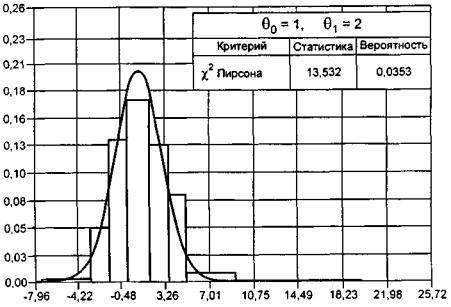
Рисунок 15 - Результаты проверки согласия к примеру 3
Пример 4 Проверяют
сложную гипотезу о принадлежности выборки нормальному закону распределения. По
выборке оценивают параметр сдвига. Параметр масштаба θ 1 = 2.
Выборка из примера 3.
Вычисленная по ней оценка максимального правдоподобия параметра сдвига θ 0 = 1,2097.
Оставляют k = 7, так как из таблицы А.25
Pk Ч n = 0,0536Ч300 > 15. Оптимальные граничные
точки в виде ti = (х i - θ0)θ 1 берут из таблицы А.24 (-1,6108; -0,8744; -0,2803; 0,2803; 0,8744;
1,6108). При θ 0 = 1,2097; θ 1 = 2х i принимают значения -2,0119; -0,5391; 0,6491;
1,7703; 2,9585; 4,4313. Вероятности попадания наблюдений в интервал из таблицы А.25:
0,0536; 0,1373; 0,1987; 0,2208; 0,1987; 0,1373; 0,0536. По выборке находят
числа наблюдений ni , попавших в соответствующие интервалы (13, 58,
53, 62, 48, 33, 23). В соответствии с соотношением ( 1 ) вычисляют значение статистики ![]() При справедливости H 0 статистика
приближенно подчиняется
При справедливости H 0 статистика
приближенно подчиняется ![]() - распределению. Вероятность
- распределению. Вероятность ![]() При значениях уровня
значимости α > 0,0173 гипотеза H 0 будет отклонена. Результаты проверки
гипотезы о согласии иллюстрирует рисунок 16.
При значениях уровня
значимости α > 0,0173 гипотеза H 0 будет отклонена. Результаты проверки
гипотезы о согласии иллюстрирует рисунок 16.
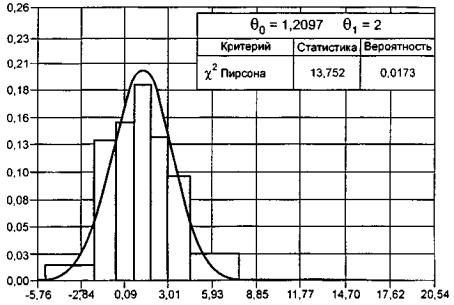
Рисунок 16 - Результаты проверки согласия к примеру 4
Пример 5 Проверяют
сложную гипотезу о принадлежности выборки нормальному закону распределения. По
выборке оценивают масштабный параметр (стандартное отклонение). Параметр сдвига
θ 0 = 1. Выборка из примера 3.
Вычисленная по ней оценка максимального правдоподобия параметра масштаба θ 0 = 2,1101.
Выбирают k = 5, так как из таблицы А.27 P k Ч n = 0,023Ч300 > 6 и при большем числе интервалов ожидаемое число
попаданий наблюдений в крайние интервалы не превышает 3. Оптимальные граничные
точки в виде ti = (х i - θ0)θ 1 , берут из таблицы А.26 : -1,9956; -1,1401; 1,1401; 1,9958. При θ 0 = 1, θ 1 = 2,1101х i принимают значения -3,21092; -1,40573;
3,405725; 5,211338. Вероятности попадания наблюдений в интервал из таблицы А.27 : 0,0230; 0,1041; 0,7458; 0,1041; 0,0230. По
выборке находят числа наблюдений ni , попавших в соответствующие интервалы (3, 29,
221, 41, 9). В соответствии с соотношением ( 1 ) вычисляют значение статистики ![]() При справедливости H 0 статистика
приближенно подчиняется
При справедливости H 0 статистика
приближенно подчиняется ![]() - распределению. Вероятность
- распределению. Вероятность ![]() При значениях уровня
значимости α < 0,1 нет оснований для отклонения гипотезы H 0 . Результаты
проверки гипотезы о согласии показаны на рисунке 17.
При значениях уровня
значимости α < 0,1 нет оснований для отклонения гипотезы H 0 . Результаты
проверки гипотезы о согласии показаны на рисунке 17.
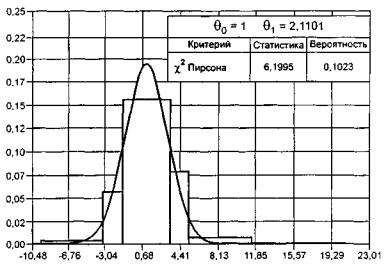
Рисунок 17 - Результаты проверки согласия к примеру 5
Пример 6 Проверяют
сложную гипотезу о принадлежности наблюдаемой выборки нормальному закону
распределения. Проверяемая гипотеза имеет вид  По выборке из примера
3
оценивают оба параметра нормального распределения. Оценки максимального
правдоподобия параметров при θ 0 = 1,2097; θ 1 = 2,1032. Как и в примере 3,
оптимальные граничные точки в виде ti = (х i - θ0)θ 1 берут из таблицы
А.28 при k = 7
(-2,0600; -1,2647; -0,4918; 0,4918; 1,2647; 2,0600), так как из таблицы А.29 P k Ч n = 0,0197Ч300 > 5. При θ0
= 1,2097; θ1 = 2,1032х i принимают значения -3,1435; -1,4629; 0,1704;
2,2490; 3,8823; 5,5629. Вероятности попадания наблюдений в интервал из таблицы А.29 : 0,0197; 0,0833; 0,2084; 0,3772; 0,2084;
0,0833; 0,0197. По выборке находят числа наблюдений ni , попавших в соответствующие интервалы (3,
29, 67, 105, 64, 26, 6). В соответствии с соотношением ( 1 ) вычисляют значение статистики
По выборке из примера
3
оценивают оба параметра нормального распределения. Оценки максимального
правдоподобия параметров при θ 0 = 1,2097; θ 1 = 2,1032. Как и в примере 3,
оптимальные граничные точки в виде ti = (х i - θ0)θ 1 берут из таблицы
А.28 при k = 7
(-2,0600; -1,2647; -0,4918; 0,4918; 1,2647; 2,0600), так как из таблицы А.29 P k Ч n = 0,0197Ч300 > 5. При θ0
= 1,2097; θ1 = 2,1032х i принимают значения -3,1435; -1,4629; 0,1704;
2,2490; 3,8823; 5,5629. Вероятности попадания наблюдений в интервал из таблицы А.29 : 0,0197; 0,0833; 0,2084; 0,3772; 0,2084;
0,0833; 0,0197. По выборке находят числа наблюдений ni , попавших в соответствующие интервалы (3,
29, 67, 105, 64, 26, 6). В соответствии с соотношением ( 1 ) вычисляют значение статистики ![]() При справедливости
гипотезы H 0 статистика приближенно подчиняется
При справедливости
гипотезы H 0 статистика приближенно подчиняется ![]() - распределению. Вычисленное значение
вероятности
- распределению. Вычисленное значение
вероятности ![]() подтверждает хорошее
согласие экспериментальных данных теоретическому распределению по данному
критерию. При значениях уровня значимости α < 0,5221 гипотеза H 0 будет принята.
Результаты проверки гипотезы о согласии иллюстрирует рисунок 18.
подтверждает хорошее
согласие экспериментальных данных теоретическому распределению по данному
критерию. При значениях уровня значимости α < 0,5221 гипотеза H 0 будет принята.
Результаты проверки гипотезы о согласии иллюстрирует рисунок 18.
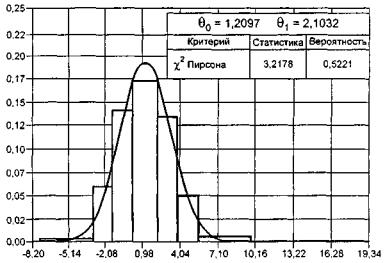
Рисунок 18 - Результаты проверки согласия к примеру 6
Пример 7 Проверяют сложную гипотезу о принадлежности выборки, представленной в примере 2, распределению Вейбулла. Проверяют гипотезу
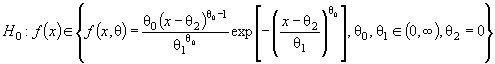
при оценивании по выборке параметров θ 0 и θ 1 методом
максимального правдоподобия. Вычисленные оценки θ 0 = 1,2585, θ 1 = 1,0088. Из условия, чтобы ожидаемое число
наблюдений, попавших в интервал с наименьшей вероятностью, было не очень малым,
по таблице А.23
выбирают k = 6. В этом случае P k Ч n = 0,0122Ч300 > 3. Оптимальные граничные
точки в виде ![]() берут из таблицы А.22:
0,0772; 0,3649; 1,2269; 2,5726; 4,4096. При θ 0 = 1,2585; θ 1 =1,0088; θ 2 = 0 по значениям ti определяют
берут из таблицы А.22:
0,0772; 0,3649; 1,2269; 2,5726; 4,4096. При θ 0 = 1,2585; θ 1 =1,0088; θ 2 = 0 по значениям ti определяют 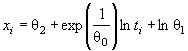 : 0,1318; 0,4528; 1,1868; 2,1374; 3,2798. Вероятности
попадания наблюдений в интервал из таблицы А.23:
0,0743; 0,2314; 0,4011; 0,2169; 0,0641; 0,0122. По выборке находят числа
наблюдений ni , попавших в соответствующие интервалы (24, 69, 116, 67, 21, 3).
: 0,1318; 0,4528; 1,1868; 2,1374; 3,2798. Вероятности
попадания наблюдений в интервал из таблицы А.23:
0,0743; 0,2314; 0,4011; 0,2169; 0,0641; 0,0122. По выборке находят числа
наблюдений ni , попавших в соответствующие интервалы (24, 69, 116, 67, 21, 3).
Значение статистики ![]() При справедливости
гипотезы H 0 статистика приближенно подчиняется
При справедливости
гипотезы H 0 статистика приближенно подчиняется ![]() - распределению. Так
как вычисленная вероятность
- распределению. Так
как вычисленная вероятность ![]() то это
свидетельствует об очень хорошем согласии данных с теоретическим
распределением. Результаты проверки гипотезы иллюстрирует рисунок 19.
то это
свидетельствует об очень хорошем согласии данных с теоретическим
распределением. Результаты проверки гипотезы иллюстрирует рисунок 19.
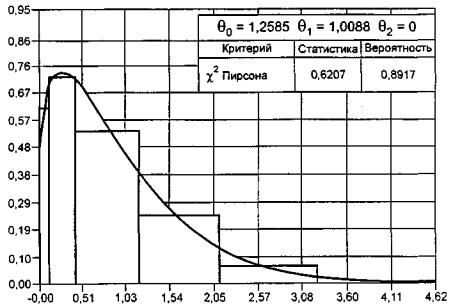
Рисунок 19 - Результаты проверки согласия к примеру 7
3 Порядок применения критериев типа χ2
3.1 Порядок проверки простой гипотезы
При проверке простой гипотезы о согласии опытного распределения с теоретическим распределением случайной величины X действуют следующим образом.
а) Формулируют проверяемую гипотезу, выбирая теоретическое распределение случайной величины F ( x , θ ), согласие которого с опытным распределением этой величины следует проверить.
б) Из совокупности отбирают случайную выборку объема N .
в) В зависимости от объема выборки N в соответствии с рекомендациями 2.8 выбирают число интервалов k .
г) Выбирают граничные точки интервалов группирования.
1) Интервалы можно выбирать равной длины, в этом случае необходимо подсчитать число ni и определить значения вероятностей Pi ( θ ).
2) Интервалы можно выбирать равновероятными, тогда Pi ( θ ) = 1/ k , но необходимо вычислить значения граничных точек х i , разделяющих интервалы.
3) Можно разбивать выборку на интервалы в соответствии с асимптотически оптимальным группированием для данного закона распределения (см. 2.9, таблицу 3). Такое разбиение наиболее предпочтительно, так как повышает способность критерия различать близкие гипотезы.
д) После подсчета ni и Pi ( θ ) в соответствии с выбранным критерием проверки вычисляют значение статистики S * критерия по формуле ( 1 ) или ( 6).
е) В соответствии с ![]() - распределением по формуле ( 5) вычисляют значение P { S > S * }. Если P { S > S * } > α, где α - задаваемый уровень значимости, то нет
оснований для отклонения проверяемой гипотезы. В противном случае проверяемую
гипотезу H 0 отвергают.
- распределением по формуле ( 5) вычисляют значение P { S > S * }. Если P { S > S * } > α, где α - задаваемый уровень значимости, то нет
оснований для отклонения проверяемой гипотезы. В противном случае проверяемую
гипотезу H 0 отвергают.
Можно вычисленное значение
статистики S * сравнить с критическим значением Sr ,α , где 1 r = k - 1 - число степеней свободы, определяемым из уравнения 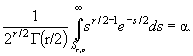 Значения Sr ,α приведены в приложении Б. Гипотезу о согласии
отвергают, если значение статистики попадает в критическую область, т. е. при S * > Sr ,α .
Значения Sr ,α приведены в приложении Б. Гипотезу о согласии
отвергают, если значение статистики попадает в критическую область, т. е. при S * > Sr ,α .
3.2 Порядок проверки сложной гипотезы
3.2.1 При проверке сложной гипотезы и вычислении оценок параметров по группированным данным в результате минимизации статистик, задаваемых формулами ( 1 ) и ( 6), или в результате максимизации функции правдоподобия ( 8) порядок проверки аналогичен случаю простой гипотезы (см. 3.1) с заданием числа степеней свободы r = k - m - 1, где m - число оцененных по данной выборке параметров. При этом остаются в силе рекомендации по способам группирования.
3.2.2 При проверке сложной гипотезы и вычислении оценок максимального правдоподобия по исходным негруппированным выборочным данным и использовании для проверки гипотезы статистики ( 11) число степеней свободы предельного распределения r = k - 1.
3.2.3 При вычислении оценок максимального правдоподобия по исходным негруппированным выборочным данным и применении для проверки гипотезы статистики, определяемой формулой ( 1 ) или ( 6), руководствуются следующими соображениями.
3.2.3.1 Значения Sr ,α процентных точек ![]() - распределения при
числе степеней свободы r = k - m - 1 меньше, чем значения процентных точек
действительных предельных распределений статистик ( 1 ) и ( 6)
для такой ситуации (см. 2.7).
Поэтому, если S * < Sr ,α , то гипотеза H 0 о согласии при заданном уровне значимости α заведомо не должна
быть отвергнута.
- распределения при
числе степеней свободы r = k - m - 1 меньше, чем значения процентных точек
действительных предельных распределений статистик ( 1 ) и ( 6)
для такой ситуации (см. 2.7).
Поэтому, если S * < Sr ,α , то гипотеза H 0 о согласии при заданном уровне значимости α заведомо не должна
быть отвергнута.
3.2.3.2 Значения процентных
точек действительных распределений статистик ( 1 ) и ( 6) существенно отличаются
от процентных точек ![]() - распределения при числе степеней
свободы r = k - m - 1.
- распределения при числе степеней
свободы r = k - m - 1.
При больших значениях S * вероятности вида P { S > S * }, вычисляемые в
соответствии с ![]() - распределением по формуле ( 5), достаточно близки к вероятностям P { S > S * }, соответствующим действительным распределениям статистик.
- распределением по формуле ( 5), достаточно близки к вероятностям P { S > S * }, соответствующим действительным распределениям статистик.
При малых значениях S * вероятности, вычисляемые по формуле ( 5), много меньше действительных значений P { S > S * } (см. 2.7). Поэтому, если приближенное значение, вычисленное по формуле ( 5), больше значения α, то заведомо P { S > S * } > α и гипотеза о согласии не должна быть отвергнута.
ПРИЛОЖЕНИЕ А
(рекомендуемое)
Таблицы асимптотически оптимального группирования наблюдений в критериях согласия типа χ2
Таблица А.1 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании параметра экспоненциального распределения, параметра распределения Парето, масштабного параметра распределения Вейбулла, параметра сдвига распределения наименьшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
A |
|
2 |
1,5936 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
3 |
1,0176 |
2,6112 |
- |
_ |
- |
- |
- |
- |
- |
- |
0,8203 |
|
4 |
0,7541 |
1,7716 |
3,3652 |
- |
- |
- |
- |
- |
- |
- |
0,8910 |
|
5 |
0,6004 |
1,3545 |
2,3720 |
3,9657 |
- |
- |
- |
- |
- |
- |
0,9269 |
|
6 |
0,4993 |
1,0997 |
1,8538 |
2,8714 |
4,4650 |
- |
- |
- |
- |
- |
0,9606 |
|
7 |
0,4276 |
0,9269 |
1,5273 |
2,2813 |
3,2989 |
4,8925 |
- |
- |
- |
- |
0,9606 |
|
8 |
0,3739 |
0,8015 |
1,3008 |
1,9012 |
2,6553 |
3,6729 |
5,2665 |
- |
- |
- |
0,9693 |
|
9 |
0,3323 |
0,7063 |
1,1338 |
1,6331 |
2,2336 |
2,9876 |
4,0052 |
5,5988 |
- |
- |
0,9754 |
|
10 |
0,2990 |
0,6314 |
1,0053 |
1,4329 |
1,9322 |
2,5326 |
3,2866 |
4,3042 |
5,8979 |
- |
0,9798 |
|
11 |
0,2716 |
0,5695 |
0,9014 |
1,2746 |
1,7015 |
2,1989 |
2,7955 |
3,5429 |
4,5480 |
6,1176 |
0,9832 |
Таблица А.2 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра экспоненциального распределения, параметра распределения Рэлея, параметра распределения Парето, масштабного параметра распределения Вейбулла, параметра сдвига распределения наименьшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
A |
|
2 |
0,7968 |
0,2032 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
3 |
0,6385 |
0,2880 |
0,0735 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8203 |
|
4 |
0,5296 |
0,3004 |
0,1355 |
0,0345 |
- |
- |
- |
- |
- |
- |
- |
0,8911 |
|
5 |
0,4514 |
0,2905 |
0,1648 |
0,0744 |
0,0189 |
- |
- |
- |
- |
- |
- |
0,9269 |
|
6 |
0,3930 |
0,2740 |
0,1763 |
0,1000 |
0,0451 |
0,0116 |
- |
- |
- |
- |
- |
0,9476 |
|
7 |
0,3479 |
0,2563 |
0,1787 |
0,1150 |
0,0652 |
0,0294 |
0,0075 |
- |
- |
- |
- |
0,9606 |
|
8 |
0,3120 |
0,2394 |
0,1763 |
0,1229 |
0,0791 |
0,0449 |
0,0202 |
0,0052 |
- |
- |
- |
0,9693 |
|
9 |
0,2827 |
0,2238 |
0,1717 |
0,1265 |
0,0882 |
0,0567 |
0,0322 |
0,0145 |
0,0037 |
- |
- |
0,9754 |
|
10 |
0,2584 |
0,2097 |
0,1659 |
0,1273 |
0,0938 |
0,0654 |
0,0421 |
0,0239 |
0,0107 |
0,0028 |
- |
0,9798 |
|
11 |
0,2378 |
0,1964 |
0,1598 |
0,1264 |
0,0971 |
0,0715 |
0,0498. |
0,0322 |
0,0183 |
0,0083 |
0,0024 |
0,9832 |
Таблица А.3 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании параметра распределения Рэлея) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
1,7853 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
3 |
1,4266 |
2,2853 |
- |
- |
- |
- |
- |
- |
- |
0,8203 |
|
4 |
1,2280 |
1,8823 |
2,5943 |
- |
- |
- |
- |
- |
- |
0,8910 |
|
5 |
1,0954 |
1,6459 |
2,1781 |
2,8163 |
- |
- |
- |
- |
- |
0,9269 |
|
6 |
0,9993 |
1,4831 |
1,9255 |
2,3964 |
2,9883 |
- |
- |
- |
- |
0,9476 |
|
7 |
0,9247 |
1,3615 |
1,7477 |
2,1360 |
2,5686 |
3,1281 |
- |
- |
- |
0,9606 |
|
8 |
0,8648 |
1,2661 |
1,6130 |
1,9500 |
2,3045 |
2,7103 |
3,2455 |
- |
- |
0,9693 |
|
9 |
0,8152 |
1,1884 |
1,5058 |
1,8073 |
2,1136 |
2,4444 |
2,8303 |
3,3463 |
- |
0,9754 |
|
10 |
0,7734 |
1,1237 |
1,4180 |
1,6928 |
1,9658 |
2,2506 |
2,5638 |
2,9340 |
3,4344 |
0,9798 |
Таблица А.4 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании параметра распределения Максвелла) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
2,0451 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6451 |
|
3 |
1,6762 |
2,5366 |
- |
- |
- |
- |
- |
- |
- |
0,8179 |
|
4 |
1,4689 |
2,1292 |
2,8402 |
- |
- |
- |
- |
- |
- |
0,8892 |
|
5 |
1,3292 |
1,8879 |
2,4221 |
3,0583 |
- |
- |
- |
- |
- |
0,9254 |
|
6 |
1,2261 |
1,7205 |
2,1667 |
2,6379 |
3,2274 |
- |
- |
- |
- |
0,9464 |
|
7 |
1,1458 |
1,5947 |
1,9859 |
2,3759 |
2,8081 |
3,3649 |
- |
- |
- |
0,9596 |
|
8 |
1,0807 |
1,4952 |
1,8481 |
2,1879 |
2,5431 |
2,9480 |
3,4803 |
- |
- |
0,9685 |
|
9 |
1,0267 |
1,4138 |
1,7377 |
2,0423 |
2,3499 |
2,6803 |
3,0652 |
3,5789 |
- |
0,9747 |
|
10 |
0,9798 |
1,3447 |
1,6460 |
1,9252 |
2,2003 |
2,4857 |
2,7984 |
3,1668 |
3,6625 |
0,9792 |
Таблица А.5 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Максвелла) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,7576 |
0,2424 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6451 |
|
3 |
0,5781 |
0,3296 |
0,0923 |
- |
- |
- |
- |
- |
- |
- |
0,8179 |
|
4 |
0,4597 |
0,3310 |
0,1647 |
0,0446 |
- |
- |
- |
- |
- |
- |
0,8892 |
|
5 |
0,3778 |
0,3097 |
0,1942 |
0,0933 |
0,0250 |
- |
- |
- |
- |
- |
0,9254 |
|
6 |
0,3185 |
0,2837 |
0,2022 |
0,1223 |
0,0579 |
0,0154 |
- |
- |
- |
- |
0,9464 |
|
7 |
0,2739 |
0,2585 |
0,2000 |
0,1374 |
0,0818 |
0,0383 |
0,0101 |
- |
- |
- |
0,9596 |
|
8 |
0,2393 |
0,2357 |
0,1931 |
0,1438 |
0,0971 |
0,0573 |
0,0267 |
0,0070 |
- |
- |
0,9685 |
|
9 |
0,2119 |
0,2155 |
0,1840 |
0,1450 |
0,1063 |
0,0711 |
0,0418 |
0,0194 |
0,0050 |
- |
0,9747 |
|
10 |
0,1891 |
0,1978 |
0,1745 |
0,1437 |
0,1112 |
0,0806 |
0,0536 |
0,0313 |
0,0145 |
0,0038 |
0,9792 |
Таблица А.6 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании параметра полунормального распределения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
1,4821 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6523 |
|
3 |
1,1395 |
1,9952 |
- |
- |
- |
- |
- |
- |
- |
0,8244 |
|
4 |
0,9553 |
1,5993 |
2,3124 |
- |
- |
- |
- |
- |
- |
0,8943 |
|
5 |
0,8355 |
1,3712 |
1,9002 |
2,5407 |
- |
- |
- |
- |
- |
0,9295 |
|
6 |
0,7495 |
1,2163 |
1,6526 |
2,1225 |
2,7173 |
- |
- |
- |
- |
0,9496 |
|
7 |
0,6842 |
1,1025 |
1,4797 |
1,8658 |
2,3009 |
2,8632 |
- |
- |
- |
0,9622 |
|
8 |
0,6277 |
1,0069 |
1,3432 |
1,6751 |
2,0278 |
2,4343 |
2,9742 |
- |
- |
0,9706 |
|
9 |
0,5892 |
0,9409 |
1,2488 |
1,5445 |
1,8503 |
2,1861 |
2,5844 |
3,1015 |
- |
0,9765 |
|
10 |
0,5545 |
0,8838 |
1,1682 |
1,4380 |
1,7113 |
2,0012 |
2,3249 |
2,6993 |
3,2125 |
0,9808 |
Таблица А.7 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании параметра полунормального распределения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,8617 |
0,1383 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6523 |
|
3 |
0,7455 |
0,2085 |
0,0460 |
- |
- |
- |
- |
- |
- |
- |
0,8244 |
|
4 |
0,6606 |
0,2297 |
0,0890 |
0,0207 |
- |
- |
- |
- |
- |
- |
0,8943 |
|
5 |
0,5966 |
0,2331 |
0,1129 |
0,0463 |
0,0111 |
- |
- |
- |
- |
- |
0,9295 |
|
6 |
0,5464 |
0,2297 |
0,1255 |
0,0646 |
0,0272 |
0,0066 |
- |
- |
- |
- |
0,9496 |
|
7 |
0,5061 |
0,2236 |
0,1313 |
0,0769 |
0,0407 |
0,0172 |
0,0042 |
- |
- |
- |
0,9622 |
|
8 |
0,4698 |
0,2162 |
0,1348 |
0,0853 |
0,0513 |
0,0277 |
0,0120 |
0,0029 |
- |
- |
0,9706 |
|
9 |
0,4443 |
0,2090 |
0,1350 |
0,0893 |
0,0582 |
0,0355 |
0,0190 |
0,0078 |
0,0019 |
- |
0,9765 |
|
10 |
0,4208 |
0,2024 |
0,1341 |
0,0923 |
0,0634 |
0,0417 |
0,0253 |
0,0131 |
0,0056 |
0,0013 |
0,9808 |
Таблица А.8 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 4)] и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
2,2759 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6435 |
|
3 |
1,9011 |
2,7621 |
- |
- |
- |
- |
- |
- |
- |
0,8164 |
|
4 |
1,6877 |
2,3523 |
3,0619 |
- |
- |
- |
- |
- |
- |
0,8880 |
|
5 |
1,5409 |
2,1027 |
2,6375 |
3,2731 |
- |
- |
- |
- |
- |
0,9245 |
|
6 |
1,4320 |
1,9320 |
2,3793 |
2,8420 |
3,4371 |
- |
- |
- |
- |
0,9456 |
|
7 |
1,3441 |
1,7985 |
2,1899 |
2,5797 |
3,0076 |
3,5655 |
- |
- |
- |
0,9589 |
|
8 |
1,2773 |
1,6988 |
2,0537 |
2,3944 |
2,7499 |
3,1553 |
3,6866 |
- |
- |
0,9679 |
|
9 |
1,2376 |
1,6331 |
1,9559 |
2,2567 |
2,5594 |
2,8931 |
3,2773 |
3,7885 |
- |
0,9742 |
|
10 |
1,1957 |
1,5742 |
1,8805 |
2,1615 |
2,4364 |
2,7194 |
3,0318 |
3,3999 |
3,8922 |
0,9788 |
Таблица А.9 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 4)] и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,7306 |
0,2694 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6435 |
|
3 |
0,5393 |
0,3546 |
0,1061 |
- |
- |
- |
- |
- |
- |
- |
0,8164 |
|
4 |
0,4165 |
0,3467 |
0,1844 |
0,0524 |
- |
- |
- |
- |
- |
- |
0,8880 |
|
5 |
0,3327 |
0,3153 |
0,2138 |
0,1082 |
0,0300 |
- |
- |
- |
- |
- |
0,9245 |
|
6 |
0,2736 |
0,2830 |
0,2175 |
0,1383 |
0,0688 |
0,0188 |
- |
- |
- |
- |
0,9456 |
|
7 |
0,2287 |
0,2519 |
0,2105 |
0,1536 |
0,0953 |
0,0427 |
0,0128 |
- |
- |
- |
0,9589 |
|
8 |
0,1969 |
0,2260 |
0,1997 |
0,1574 |
0,1110 |
0,0678 |
0,0325 |
0,0087 |
- |
- |
0,9679 |
|
9 |
0,1790 |
0,2060 |
0,1849 |
0,1522 |
0,1163 |
0,0827 |
0,0493 |
0,0234 |
0,0062 |
- |
0,9742 |
|
10 |
0,1610 |
0,1905 |
0,1762 |
0,1498 |
0,1187 |
0,0875 |
0,0599 |
0,0355 |
0,0165 |
0,0044 |
0,9788 |
Таблица А.10 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 5)] и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
2,4851 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6424 |
|
3 |
2,1047 |
2,9667 |
- |
- |
- |
- |
- |
- |
- |
0,8154 |
|
4 |
1,8861 |
2,5542 |
3,2635 |
- |
- |
- |
- |
- |
- |
0,8871 |
|
5 |
1,7383 |
2,3089 |
2,8453 |
3,4778 |
- |
- |
- |
- |
- |
0,9238 |
|
6 |
1,6274 |
2,1357 |
2,5880 |
3,0606 |
3,6463 |
- |
- |
- |
- |
0,9451 |
|
7 |
1,5434 |
2,0084 |
2,4056 |
2,7983 |
3,2306 |
3,7856 |
- |
- |
- |
0,9585 |
|
8 |
1,4642 |
1,8929 |
2,2499 |
2,5904 |
2,9449 |
3,3472 |
3,8734 |
- |
- |
0,9676 |
|
9 |
1,4122 |
1,8192 |
2,1563 |
2,4668 |
2,7770 |
3,1092 |
3,4938 |
4,0021 |
- |
0,9739 |
|
10 |
1,3523 |
1,7371 |
2,0514 |
2,3376 |
2,6193 |
2,9121 |
3,2278 |
3,6023 |
4,1009 |
0,9786 |
Таблица А.11 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 5)] и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,7105 |
0,2895 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6424 |
|
3 |
0,5106 |
0,3721 |
0,1173 |
- |
- |
- |
- |
- |
- |
- |
0,8154 |
|
4 |
0,3853 |
0,3562 |
0,1997 |
0,0588 |
- |
- |
- |
- |
- |
- |
0,8871 |
|
5 |
0,3033 |
0,3199 |
0,2258 |
0,1175 |
0,0335 |
- |
- |
- |
- |
- |
0,9238 |
|
6 |
0,2460 |
0,2822 |
0,2276 |
0,1489 |
0,0745 |
0,0208 |
- |
- |
- |
- |
0,9451 |
|
7 |
0,2059 |
0,2495 |
0,2171 |
0,1617 |
0,1021 |
0,0501 |
0,0136 |
- |
- |
- |
0,9585 |
|
8 |
0,1711 |
0,2181 |
0,2025 |
0,1653 |
0,1202 |
0,0754 |
0,0371 |
0,0103 |
- |
- |
0,9676 |
|
9 |
0,1501 |
0,1975 |
0,1923 |
0,1620 |
0,1252 |
0,0876 |
0,0532 |
0,0253 |
0,0068 |
- |
0,9739 |
|
10 |
0,1277 |
0,1750 |
0,1774 |
0,1580 |
0,1307 |
0,0995 |
0,0675 |
0,0406 |
0,0187 |
0,0049 |
0,9786 |
Таблица А.12 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 6)] и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
2,6788 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6416 |
|
3 |
2,2937 |
3,1562 |
- |
- |
- |
- |
- |
- |
- |
0,8146 |
|
4 |
2,0690 |
2,7373 |
3,4474 |
- |
- |
- |
- |
- |
- |
0,8865 |
|
5 |
1,9209 |
2,4937 |
3,0329 |
3,6644 |
- |
- |
- |
- |
- |
0,9233 |
|
6 |
1,8077 |
2,3206 |
2,7794 |
3,2560 |
3,8376 |
- |
- |
- |
- |
0,9446 |
|
7 |
1,7052 |
2,1822 |
2,5885 |
2,9928 |
3,4297 |
3,9772 |
- |
- |
- |
0,9581 |
|
8 |
1,6448 |
2,0820 |
2,4474 |
2,7948 |
3,1545 |
3,5620 |
4,0856 |
- |
- |
0,9673 |
|
9 |
1,5655 |
1,9772 |
2,3189 |
2,6446 |
2,9689 |
3,3159 |
3,7061 |
4,2064 |
- |
0,9736 |
|
10 |
1,5219 |
1,9135 |
2,2322 |
2,5258 |
2,8116 |
3,1058 |
3,4252 |
3,7974 |
4,2833 |
0,9784 |
Таблица А.13 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 6)] и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,6951 |
0,3049 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6416 |
|
3 |
0,4892 |
0,3845 |
0,1263 |
- |
- |
- |
- |
- |
- |
- |
0,8146 |
|
4 |
0,3612 |
0,3611 |
0,2131 |
0,0646 |
- |
- |
- |
- |
- |
- |
0,8865 |
|
5 |
0,2815 |
0,3194 |
0,2364 |
0,1260 |
0,0367 |
- |
- |
- |
- |
- |
0,9233 |
|
6 |
0,2254 |
0,2791 |
0,2365 |
0,1575 |
0,0790 |
0,0225 |
- |
- |
- |
- |
0,9446 |
|
7 |
0,1797 |
0,2456 |
0,2253 |
0,1734 |
0,1085 |
0,0528 |
0,0147 |
- |
- |
- |
0,9581 |
|
8 |
0,1552 |
0,2133 |
0,2071 |
0,1721 |
0,1255 |
0,0785 |
0,0378 |
0,0105 |
- |
- |
0,9673 |
|
9 |
0,1261 |
0,1850 |
0,1925 |
0,1750 |
0,1371 |
0,0958 |
0,0558 |
0,0256 |
0,0071 |
- |
0,9736 |
|
10 |
0,1115 |
0,1661 |
0,1764 |
0,1640 |
0,1369 |
0,1048 |
0,0721 |
0,0429 |
0,0199 |
0,0054 |
0,9784 |
Таблица А.14 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 7)] и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
2,8592 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6410 |
|
3 |
2,4702 |
3,3335 |
- |
- |
- |
- |
- |
- |
- |
0,8141 |
|
4 |
2,2424 |
2,9130 |
3,6227 |
- |
- |
- |
- |
- |
- |
0,8861 |
|
5 |
2,0892 |
2,6637 |
3,2017 |
3,8338 |
- |
- |
- |
- |
- |
0,9229 |
|
6 |
1,9753 |
2,4906 |
2,9522 |
3,4307 |
4,0111 |
- |
- |
- |
- |
0,9444 |
|
7 |
1,8697 |
2,3537 |
2,7638 |
3,1754 |
3,6180 |
4,1618 |
- |
- |
- |
0,9579 |
|
8 |
1,8095 |
2,2496 |
2,6140 |
2,9589 |
3,3148 |
3,7168 |
4,2420 |
- |
- |
0,9671 |
|
9 |
1,7284 |
2,1442 |
2,4877 |
2,8152 |
3,1416 |
3,4897 |
3,8810 |
4,3795 |
- |
0,9734 |
|
10 |
1,6738 |
2,0692 |
2,3912 |
2,6935 |
2,9861 |
3,2910 |
3,6147 |
3,9779 |
4,4670 |
0,9782 |
Таблица А.15 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 7)] и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,6826 |
0,3174 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6410 |
|
3 |
0,4720 |
0,3942 |
0,1338 |
- |
- |
- |
- |
- |
- |
- |
0,8141 |
|
4 |
0,3435 |
0,3648 |
0,2226 |
0,0691 |
- |
- |
- |
- |
- |
- |
0,8861 |
|
5 |
0,2631 |
0,3179 |
0,2442 |
0,1347 |
0,0401 |
- |
- |
- |
- |
- |
0,9229 |
|
6 |
0,2090 |
0,3866 |
0,1307 |
0,1653 |
0,0841 |
0,0243 |
- |
- |
- |
- |
0,9444 |
|
7 |
0,1643 |
0,2413 |
0,2288 |
0,1816 |
0,1140 |
0,0545 |
0,0155 |
- |
- |
- |
0,9579 |
|
8 |
0,1414 |
0,2059 |
0,2061 |
0,1758 |
0,1316 |
0,0846 |
0,0426 |
0,0120 |
- |
- |
0,9671 |
|
9 |
0,1138 |
0,1772 |
0,1910 |
0,1787 |
0,1432 |
0,1012 |
0,0597 |
0,0276 |
0,0076 |
- |
0,9734 |
|
10 |
0,0972 |
0,1559 |
0,1738 |
0,1702 |
0,1441 |
0,1237 |
0,0645 |
0,0438 |
0,0211 |
0,0057 |
0,9782 |
Таблица А.16 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 8)] и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
3,0289 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6405 |
|
3 |
2,6345 |
3,4992 |
- |
- |
- |
- |
- |
- |
- |
0,8136 |
|
4 |
2,4103 |
3,0825 |
3,7907 |
- |
- |
- |
- |
- |
- |
0,8857 |
|
5 |
2,2556 |
2,8342 |
3,3745 |
4,0004 |
- |
- |
- |
- |
- |
0,9226 |
|
6 |
2,1318 |
2,6542 |
3,1120 |
3,5661 |
4,1522 |
- |
- |
- |
- |
0,9441 |
|
7 |
2,0383 |
2,5119 |
2,9189 |
3,3178 |
3,7560 |
4,3031 |
- |
- |
- |
0,9577 |
|
8 |
1,9612 |
2,4048 |
2,7742 |
3,1251 |
3,4917 |
3,8964 |
4,4313 |
- |
- |
0,9669 |
|
9 |
1,8989 |
2,3089 |
2,6432 |
2,9523 |
3,2672 |
3,6044 |
3,9900 |
4,4952 |
- |
0,9734 |
|
10 |
1,8477 |
2,2411 |
2,5569 |
2,8434 |
3,1248 |
3,4169 |
3,7366 |
4,1059 |
4,5926 |
0,9781 |
Таблица А.17 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 8)] и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,6722 |
0,3278 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6405 |
|
3 |
0,4569 |
0,4024 |
0,1407 |
- |
- |
- |
- |
- |
- |
- |
0,8136 |
|
4 |
0,3314 |
0,3668 |
0,2292 |
0,0726 |
- |
- |
- |
- |
- |
- |
0,8857 |
|
5 |
0,2518 |
0,3179 |
0,2496 |
0,1384 |
0,0423 |
- |
- |
- |
- |
- |
0,9226 |
|
6 |
0,1950 |
0,2732 |
0,2439 |
0,1659 |
0,0944 |
0,0276 |
- |
- |
- |
- |
0,9441 |
|
7 |
0,1571 |
0,2303 |
0,2282 |
0,1831 |
0,1223 |
0,0614 |
0,0176 |
- |
- |
- |
0,9577 |
|
8 |
0,1293 |
0,1992 |
0,2078 |
0,1819 |
0,1390 |
0,0871 |
0,0440 |
0,0117 |
- |
- |
0,9669 |
|
9 |
0,1092 |
0,1691 |
0,1836 |
0,1713 |
0,1460 |
0,1087 |
0,0686 |
0,0339 |
0,0096 |
- |
0,9734 |
|
10 |
0,0942 |
0,1506 |
0,1680 |
0,1838 |
0,1215 |
0,1157 |
0,0835 |
0,0511 |
0,0248 |
0,0068 |
0,9781 |
Таблица А.18 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании параметра распределения модуля нормальной случайной величины ( m = 9)] и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
3,1896 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6401 |
|
3 |
2,7889 |
3,6556 |
- |
- |
- |
- |
- |
- |
- |
0,8132 |
|
4 |
2,5681 |
3,2422 |
3,9494 |
- |
- |
- |
- |
- |
- |
0,8854 |
|
5 |
2,4156 |
2,9987 |
3,5397 |
4,1663 |
- |
- |
- |
- |
- |
0,9224 |
|
6 |
2,2791 |
2,7928 |
3,2466 |
3,7175 |
4,2994 |
- |
- |
- |
- |
0,9439 |
|
7 |
2,1972 |
2,6754 |
3,0764 |
3,4674 |
3,8929 |
4,4386 |
- |
- |
- |
0,1576 |
|
8 |
2,1200 |
2,5657 |
2,9302 |
3,2748 |
3,6274 |
4,0259 |
4,5434 |
- |
- |
0,9668 |
|
9 |
2,0507 |
2,4729 |
2,8164 |
3,1248 |
3,4271 |
3,7451 |
4,1148 |
4,6058 |
- |
0,9732 |
|
10 |
2,0025 |
2,3997 |
2,7147 |
2,9993 |
3,2763 |
3,5582 |
3,8621 |
4,2153 |
4,6964 |
0,9780 |
Таблица А.19 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 [при оценивании параметра распределения модуля нормальной случайной величины ( m = 9)] и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,6634 |
0,3366 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6401 |
|
3 |
0,4433 |
0,4098 |
0,1469 |
- |
- |
- |
- |
- |
- |
- |
0,8132 |
|
4 |
0,3208 |
0,3685 |
0,2349 |
0,0758 |
- |
- |
- |
- |
- |
- |
0,8854 |
|
5 |
0,2437 |
0,3183 |
0,2529 |
0,1417 |
0,0434 |
- |
- |
- |
- |
- |
0,9224 |
|
6 |
0,1829 |
0,2626 |
0,2459 |
0,1797 |
0,0989 |
0,0300 |
- |
- |
- |
- |
0,9439 |
|
7 |
0,1509 |
0,2284 |
0,2251 |
0,1835 |
0,1253 |
0,0669 |
0,0199 |
- |
- |
- |
0,9516 |
|
8 |
0,1240 |
0,1955 |
0,2041 |
0,1813 |
0,1395 |
0,0929 |
0,0484 |
0,0143 |
- |
- |
0,9668 |
|
9 |
0,1026 |
0,1691 |
0,1873 |
0,1711 |
0,1418 |
0,1067 |
0,0716 |
0,0381 |
0,0117 |
- |
0,9732 |
|
10 |
0,0892 |
0,1469 |
0,1651 |
0,1610 |
0,1434 |
0,1158 |
0,0853 |
0,0553 |
0,0293 |
0,0087 |
0,9780 |
Таблица А.20 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании основного параметра распределения Вейбулла, масштабного параметра распределения наименьшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
3,4903 |
- |
- |
- |
- |
- |
- |
- |
- |
0,3282 |
|
3 |
0,1418 |
3,2891 |
- |
- |
- |
- |
- |
- |
- |
0,6518 |
|
4 |
0,1505 |
2,6936 |
4,5643 |
- |
- |
- |
- |
- |
- |
0,7481 |
|
5 |
0,0516 |
0,2486 |
2,6173 |
4,4970 |
- |
- |
- |
- |
- |
0,8235 |
|
6 |
0,0535 |
0,2580 |
2,3339 |
3,6005 |
5,3984 |
- |
- |
- |
- |
0,8639 |
|
7 |
0,0244 |
0,1154 |
0,3260 |
2,2878 |
3,5602 |
5,3523 |
- |
- |
- |
0,8936 |
|
8 |
0,0251 |
0,1181 |
0,3342 |
2,1205 |
3,1036 |
4,2984 |
6,0540 |
- |
- |
0,9141 |
|
9 |
0,0136 |
0,0639 |
0,1731 |
0,3843 |
2,0935 |
3,0803 |
4,2767 |
6,0333 |
- |
0,9288 |
|
10 |
0,0137 |
0,0649 |
0,1760 |
0,3917 |
1,9766 |
2,7906 |
3,7069 |
4,8673 |
6,6006 |
0,9408 |
Таблица А.21 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании основного параметра распределения Вейбулла, масштабного параметра распределения наименьшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,9695 |
0,0305 |
- |
- |
- |
- |
- |
- |
- |
- |
0,3282 |
|
3 |
0,1322 |
0,8305 |
0,0373 |
- |
- |
- |
- |
- |
- |
- |
0,6518 |
|
4 |
0,1397 |
0,7927 |
0,0572 |
0,0104 |
- |
- |
- |
- |
- |
- |
0,7481 |
|
5 |
0,0503 |
0,1698 |
0,7069 |
0,0619 |
0,0111 |
- |
- |
- |
- |
- |
0,8235 |
|
6 |
0,0521 |
0,1753 |
0,6757 |
0,0696 |
0,0228 |
0,0045 |
- |
- |
- |
- |
0,8639 |
|
7 |
0,0241 |
0,0949 |
0,1692 |
0,6203 |
0,0731 |
0,0237 |
0,0047 |
- |
- |
- |
0,8936 |
|
8 |
0,0248 |
0,0866 |
0,1727 |
0,5959 |
0,0751 |
0,0313 |
0,0113 |
0,0023 |
- |
- |
0,9141 |
|
9 |
0,0134 |
0,0465 |
0,0970 |
0,1602 |
0,5576 |
0,0774 |
0,0320 |
0,1115 |
0,0024 |
- |
0,9288 |
|
10 |
0,0136 |
0,0492 |
0,0986 |
0,1627 |
0,5374 |
0,0771 |
0,0368 |
0,0169 |
0,0063 |
0,0014 |
0,9408 |
Таблица А.22 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров распределения Вейбулла, двух параметров распределения наименьшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
t 12 |
t 13 |
t 14 |
A |
|
3 |
0,2731 |
2,6067 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4079 |
|
4 |
0,2109 |
1,3979 |
3,4137 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5572 |
|
5 |
0,1044 |
0,5123 |
1,9590 |
3,8606 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6836 |
|
6 |
0,0772 |
0,3649 |
1,2269 |
2,5726 |
4,4096 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7571 |
|
7 |
0,0501 |
0,2318 |
0,6758 |
1,7192 |
2,9922 |
4,7959 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8109 |
|
8 |
0,0377 |
0,1740 |
0,4837 |
1,1904 |
2,2041 |
3,4285 |
5,2049 |
- |
- |
- |
- |
- |
- |
- |
0,8480 |
|
9 |
0,0275 |
0,1269 |
0,3431 |
0,7829 |
1,6027 |
2,5713 |
3,7667 |
5,5273 |
- |
- |
- |
- |
- |
- |
0,8756 |
|
10 |
0,0213 |
0,0988 |
0,2638 |
0,5770 |
1,1805 |
1,9932 |
2,9269 |
4,1024 |
5,8478 |
- |
- |
- |
- |
- |
0,8963 |
|
11 |
0,0165 |
0,0771 |
0,2046 |
0,4359 |
0,8560 |
1,5344 |
2,3192 |
3,2319 |
4,3930 |
6,1270 |
- |
- |
- |
- |
0,9123 |
|
12 |
0,0123 |
0,0618 |
0,1638 |
0,3434 |
0,6517 |
1,1789 |
1,8570 |
2,6163 |
3,5103 |
4,6589 |
6,3853 |
- |
- |
- |
0,9248 |
|
13 |
0,0106 |
0,0500 |
0,1326 |
0,2754 |
0,5106 |
0,9030 |
1,4807 |
2,1401 |
2,8810 |
3,7623 |
4,9016 |
6,6208 |
- |
- |
0,9349 |
|
14 |
0,0087 |
0,0412 |
0,1094 |
0,2261 |
0,3126 |
0,7116 |
1,1798 |
1,7608 |
2,4019 |
3,1286 |
3,9997 |
5,1314 |
6,8444 |
- |
0,9431 |
|
15 |
0,0072 |
0,0344 |
0,0913 |
0,1881 |
0,3394 |
0,5734 |
0,9387 |
1,4426 |
2,0116 |
2,6381 |
3,3538 |
4,2169 |
5,3425 |
7,0506 |
0,9498 |
Таблица А.23 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров распределения Вейбулла, двух параметров распределения наименьшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
P 12 |
P 13 |
P 14 |
P 15 |
А |
|
3 |
0,2390 |
0,6872 |
0,0738 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4079 |
|
4 |
0,1901 |
0,5628 |
0,2142 |
0,0329 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5572 |
|
5 |
0,0991 |
0,3018 |
0,4581 |
0,1199 |
0,0211 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6836 |
|
6 |
0,0743 |
0,2314 |
0,4011 |
0,2169 |
0,0641 |
0,0122 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7572 |
|
7 |
0,0489 |
0,1581 |
0,2843 |
0,3295 |
0,1290 |
0,0419 |
0,0083 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8109 |
|
8 |
0,0370 |
0,1227 |
0,2238 |
0,3124 |
0,1938 |
0,0779 |
0,0269 |
0,0055 |
- |
- |
- |
- |
- |
- |
- |
0,8480 |
|
9 |
0,0271 |
0,0921 |
0,1712 |
0,2525 |
0,2557 |
0,1250 |
0,0533 |
0,0191 |
0,0040 |
- |
- |
- |
- |
- |
- |
0,8756 |
|
10 |
0,0211 |
0,0729 |
0,1379 |
0,2065 |
0,2545 |
0,1708 |
0,0827 |
0,0371 |
0,0136 |
0,0029 |
- |
- |
- |
- |
- |
0,8963 |
|
11 |
0,0164 |
0,0578 |
0,1108 |
0,1683 |
0,2218 |
0,2101 |
0,1164 |
0,0589 |
0,0271 |
0,0102 |
0,0022 |
- |
- |
- |
- |
0,9123 |
|
12 |
0,0131 |
0,0468 |
0,0912 |
0,1395 |
0,1882 |
0,2136 |
0,1515 |
0,0830 |
0,0432 |
0,0204 |
0,0078 |
0,0017 |
- |
- |
- |
0,9248 |
|
13 |
0,0105 |
0,0383 |
0,0754 |
0,1165 |
0,1592 |
0,1947 |
0,1779 |
0,1099 |
0,0615 |
0,0329 |
0,0158 |
0,0061 |
0,0013 |
- |
- |
0,9349 |
|
14 |
0,0087 |
0,0317 |
0,0632 |
0,0988 |
0,1357 |
0,1710 |
0,1836 |
0,1354 |
0,0814 |
0,0467 |
0,0255 |
0,0124 |
0,0048 |
0,0011 |
- |
0,9431 |
|
15 |
0,0072 |
0,0266 |
0,0535 |
0,0842 |
0,1163 |
0,1486 |
0,1725 |
0,1548 |
0,1025 |
0,0623 |
0,0365 |
0,0203 |
0,0099 |
0,0039 |
0,0009 |
0,9498 |
Таблица А.24 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании математического ожидания нормального распределения, параметра сдвига логарифмически нормальных распределений) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
0,0 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6336 |
|
3 |
-0,6120 |
0,6120 |
- |
- |
- |
- |
- |
- |
- |
0,8098 |
|
4 |
-0,9816 |
0,0 |
0,9816 |
- |
- |
- |
- |
- |
- |
0,8825 |
|
5 |
-1,2444 |
-0,3823 |
0,3823 |
1,2444 |
- |
- |
- |
- |
- |
0,9201 |
|
6 |
-1,4468 |
-0,6589 |
0,0 |
0,6589 |
1,4468 |
- |
- |
- |
- |
0,9420 |
|
7 |
-1,6108 |
-0,8744 |
-0,2803 |
0,2803 |
0,8744 |
1,6108 |
- |
- |
- |
0,9560 |
|
8 |
-1,7479 |
-1,0499 |
-0,5005 |
0,0 |
0,5005 |
1,0499 |
1,7479 |
- |
- |
0,9655 |
|
9 |
-1,8655 |
-1,1976 |
-0,6812 |
-0,2218 |
0,2218 |
0,6812 |
1,1976 |
1,8655 |
- |
0,9721 |
|
10 |
-1,9682 |
-1,3246 |
-0,8338 |
-0,4047 |
0,0 |
0,4047 |
0,8338 |
1,3246 |
1,9682 |
0,9771 |
Таблица А.25 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании математического ожидания нормального распределения, параметра сдвига логарифмически нормальных распределений) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,5000 |
0,5000 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6336 |
|
3 |
0,2703 |
0,4594 |
0,2703 |
- |
- |
- |
- |
- |
- |
- |
0,8098 |
|
4 |
0,1631 |
0,3369 |
0,3369 |
0,1631 |
- |
- |
- |
- |
- |
- |
0,8825 |
|
5 |
0,1067 |
0,2444 |
0,2978 |
0,2444 |
0,1067 |
- |
- |
- |
- |
- |
0,9201 |
|
6 |
0,0740 |
0,1810 |
0,2450 |
0,2450 |
0,1810 |
0,0740 |
- |
- |
- |
- |
0,9320 |
|
7 |
0,0536 |
0,1373 |
0,1987 |
0,2208 |
0,1987 |
0,1373 |
0,0536 |
- |
- |
- |
0,9560 |
|
8 |
0,0403 |
0,1066 |
0,1615 |
0,1916 |
0,1916 |
0,1615 |
0,1066 |
0,0403 |
- |
- |
0,9655 |
|
9 |
0,0310 |
0,0845 |
0,1323 |
0,1644 |
0,1756 |
0,1644 |
0,1323 |
0,0845 |
0,0310 |
- |
0,9721 |
|
10 |
0,0245 |
0,0662 |
0,1095 |
0,1406 |
0,1572 |
0,1572 |
0,1406 |
0,1095 |
0,0662 |
0,0245 |
0,9771 |
Таблица A.26 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании стандартного отклонения нормального распределения, масштабного параметра логарифмически нормальных распределений) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
-1,5750 1,5750 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,3042 0,3042 |
|
3 |
-1,4821 |
1,4821 |
- |
- |
- |
- |
- |
- |
- |
0,6522 |
|
4 |
-2,0249 -1,4520 |
-1,1865 1,1855 |
1,4520 2,0249 |
- - |
- - |
- - |
- - |
- - |
- - |
0,7358 0,7358 |
|
5 |
-1,9956 |
-1,1401 |
1,1401 |
1,9958 |
- |
- |
- |
- |
- |
0,8244 |
|
6 |
-2,3269 -1,9821 |
-1,6190 -1,1190 |
-0,9837 0,9837 |
1,1190 1,6190 |
1,9821 2,3269 |
- - |
- - |
- - |
- - |
0,8588 0,8588 |
|
7 |
-2,3130 |
-1,6002 |
-0,9558 |
0,9558 |
1,6002 |
2,3130 |
- |
- |
- |
0,8943 |
|
8 |
-2,5488 2,3053 |
-1,9105 -1,5897 |
-1,3848 -0,9400 |
-0,8548 0,8548 |
0,9400 1,3848 |
1,5897 1,9105 |
2,3053 2,5488 |
- - |
- - |
0,9117 0,9117 |
|
9 |
-2,5408 |
-1,9003 |
-1,3715 |
-0,8355 |
0,8355 |
1,3715 |
1,9003 |
2,5408 |
- |
0,9294 |
|
10 |
-2,7223 -2,5358 |
-2,1286 -1,8939 |
-1,6602 -1,3632 |
-1,2260 -0,8233 |
-0,7634 0,7634 |
0,8233 1,2260 |
1,3632 1,6602 |
1,8939 2,1286 |
2,5358 2,7223 |
0,9394 0,9394 |
Таблица А.27 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании стандартного отклонения нормального распределения, масштабного параметра логарифмически нормальных распределений) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,0576 0,9424 |
0,9424 0,0576 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,3042 0,3042 |
|
3 |
0,0692 |
0,8616 |
0,0692 |
- |
- |
- |
- |
- |
- |
- |
0,6522 |
|
4 |
0,0214 0,0732 |
0,0965 0,8089 |
0,8089 0,0965 |
0,0732 0,0214 |
- - |
- - |
- - |
- - |
- - |
- - |
0,7358 0,7358 |
|
5 |
0,0230 |
0,1041 |
0,7458 |
0,1041 |
0,0230 |
- |
- |
- |
- |
- |
0,8244 |
|
6 |
0,0100 0,0237 |
0,0427 0,1079 |
0,1099 0,7058 |
0,7058 0,1099 |
0,1079 0,0427 |
0,0237 0,0100 |
- - |
- - |
- - |
- - |
0,8588 0,8588 |
|
7 |
0,0104 |
0,0444 |
0,1148 |
0,6608 |
0,1148 |
0,0444 |
0,0104 |
- |
- |
- |
0,8943 |
|
8 |
0,0054 0,0106 |
0,0226 0,0454 |
0,0550 0,1177 |
0,1133 0,6300 |
0,6300 0,1133 |
0,1177 0,0550 |
0,0454 0,0226 |
0,0106 0,0054 |
- - |
- - |
0,9117 0,9117 |
|
9 |
0,0055 |
0,0232 |
0,0564 |
0,1166 |
0,5966 |
0,1166 |
0,0564 |
0,0232 |
0,0055 |
- |
0,9294 |
|
10 |
0,0032 0,0056 |
0,0134 0,0235 |
0,0318 0,0573 |
0,0617 0,1188 |
0,1125 0,5722 |
0,5722 0,1126 |
0,1188 0,0617 |
0,0573 0,0318 |
0,0235 0,0314 |
0,0056 0,0032 |
0,9394 0,9394 |
Таблица А.28 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров нормального распределения, двух параметров логарифмически нормальных распределений) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
t 12 |
t 13 |
t 14 |
A |
|
3 |
-1,1106 |
1,1106 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4065 |
|
4 |
-1,3834 |
0,0 |
1,3834 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5527 |
|
5 |
-1,6961 |
-0,6894 |
0,6894 |
1,6961 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6826 |
|
6 |
-1,8817 |
-0,9970 |
0,0 |
0,9970 |
1,8817 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7557 |
|
7 |
-2,0600 |
-1,2647 |
-0,4918 |
0,4918 |
1,2647 |
2,0600 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8103 |
|
8 |
-2,1954 |
-1,4552 |
-0,7863 |
0,0 |
0,7863 |
1,4552 |
2,1954 |
- |
- |
- |
- |
- |
- |
- |
0,8474 |
|
9 |
-2,3188 |
-1,6218 |
-1,0223 |
-0,3828 |
0,3828 |
1,0223 |
1,6218 |
2,3188 |
- |
- |
- |
- |
- |
- |
0,8753 |
|
10 |
-2,4225 |
-1,7578 |
-1,2046 |
-0,6497 |
0,0 |
0,6497 |
1,2046 |
1,7578 |
2,4225 |
- |
- |
- |
- |
- |
0,8960 |
|
11 |
-2,5167 |
-1,8784 |
-1,3602 |
-0,8621 |
-0,3143 |
0,3143 |
0,8621 |
1,3602 |
1,8784 |
2,5167 |
- |
- |
- |
- |
0,9121 |
|
12 |
-2,5993 |
-1,9028 |
-1,4914 |
-1,0331 |
-0,5334 |
0,0 |
0,5334 |
1,0331 |
1,4914 |
1,9028 |
2,5993 |
- |
- |
- |
0,9247 |
|
13 |
-2,6746 |
-2,0762 |
-1,6068 |
-1,1784 |
-0,7465 |
-0,2669 |
0,2669 |
0,7465 |
1,1784 |
1,6068 |
2,0762 |
2,6746 |
- |
- |
0,9348 |
|
14 |
-2,7436 |
-2,1609 |
-1,7092 |
-1,3042 |
-0,9065 |
-0,4818 |
0,0 |
0,4818 |
0,9065 |
1,3042 |
1,7092 |
2,1609 |
2,7436 |
- |
0,9430 |
|
15 |
-2,8069 |
-2,2378 |
-1,8011 |
-1,4150 |
-1,0435 |
-0,6590 |
-0,2325 |
0,2325 |
0,6590 |
1,0435 |
1,4150 |
1,8011 |
2,2378 |
2,8069 |
0,9498 |
Таблица А.29 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров нормального распределения, двух параметров логарифмически нормальных распределений) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
P 12 |
P 13 |
P 14 |
P 15 |
А |
|
3 |
0,1334 |
0,7332 |
0,1334 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4065 |
|
4 |
0,0833 |
0,4167 |
0,4167 |
0,0833 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5527 |
|
5 |
0,0449 |
0,2004 |
0,5094 |
0,2004 |
0,0449 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6826 |
|
6 |
0,0299 |
0,1295 |
0,3406 |
0,3406 |
0,1295 |
0,0299 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7557 |
|
7 |
0,0197 |
0,0833 |
0,2084 |
0,3772 |
0,2084 |
0,0833 |
0,0197 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8103 |
|
8 |
0,0141 |
0,0587 |
0,1431 |
0,2841 |
0,2841 |
0,1431 |
0,0587 |
0,0141 |
- |
- |
- |
- |
- |
- |
- |
0,8474 |
|
9 |
0,0102 |
0,0422 |
0,1009 |
0,1976 |
0,2982 |
0,1976 |
0,1009 |
0,0422 |
0,0102 |
- |
- |
- |
- |
- |
- |
0,8753 |
|
10 |
0,0077 |
0,0317 |
0,0748 |
0,1438 |
0,2420 |
0,2420 |
0,1438 |
0,0748 |
0,0317 |
0,0077 |
- |
- |
- |
- |
- |
0,8960 |
|
11 |
0,0059 |
0,0243 |
0,0567 |
0,1074 |
0,1823 |
0,2468 |
0,1823 |
0,1074 |
0,0567 |
0,0243 |
0,0059 |
- |
- |
- |
- |
0,9121 |
|
12 |
0,0047 |
0,0190 |
0,0442 |
0,0829 |
0,1392 |
0,2100 |
0,2100 |
0,1392 |
0,0829 |
0,0442 |
0,0190 |
0,0047 |
- |
- |
- |
0,9247 |
|
13 |
0,0037 |
0,0152 |
0,0352 |
0,0652 |
0,1085 |
0,1670 |
0,2104 |
0,1670 |
0,1085 |
0,0652 |
0,0352 |
0,0152 |
0,0037 |
- |
- |
0,9348 |
|
14 |
0,0030 |
0,0124 |
0,0283 |
0,0524 |
0,0862 |
0,1327 |
0,1850 |
0,1850 |
0,1327 |
0,0862 |
0,0524 |
0,0283 |
0,0124 |
0,0030 |
- |
0,9430 |
|
15 |
0,0025 |
0,0101 |
0,0232 |
0,0427 |
0,0698 |
0,1066 |
0,1532 |
0,1838 |
0,1532 |
0,1066 |
0,0698 |
0,0427 |
0,0232 |
0,0101 |
0,0025 |
0,9498 |
Таблица А.30 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании параметра сдвига распределения наибольшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
A |
|
2 |
-0,4660 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
3 |
-0,9598 |
-0,0174 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8203 |
|
4 |
-1,2135 |
-0,5719 |
0,2822 |
- |
- |
- |
- |
- |
- |
- |
0,8910 |
|
5 |
-1,3777 |
-0,8637 |
-0,3034 |
0,5102 |
- |
- |
- |
- |
- |
- |
0,9269 |
|
6 |
-1,4963 |
-1,0548 |
-0,6172 |
-0,0950 |
0,6945 |
- |
- |
- |
- |
- |
0,9476 |
|
7 |
-1,5877 |
-1,1936 |
-0,8247 |
-0,4235 |
0,0759 |
0,8496 |
- |
- |
- |
- |
0,9606 |
|
8 |
-1,6614 |
-1,3010 |
-0,9766 |
-0,6425 |
-0,2630 |
0,2213 |
0,9838 |
- |
- |
- |
0,9693 |
|
9 |
-1,7226 |
-1,3876 |
-1,0945 |
-0,8036 |
-0,1256 |
0,3477 |
1,0999 |
- |
- |
- |
0,9754 |
|
10 |
-1,7746 |
-1,4596 |
-1,1899 |
-0,9292 |
-0,6587 |
-0,3597 |
-0,0053 |
0,4598 |
1,2073 |
- |
0,9798 |
|
11 |
-1,8112 |
-1,5147 |
-1,2649 |
-1,0280 |
-0,7880 |
-0,5315 |
-0,2426 |
0,1038 |
0,5630 |
1,3034 |
0,9832 |
Таблица А.31 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании параметра сдвига распределения наибольшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
А |
|
2 |
0,2032 |
0,7968 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
3 |
0,0735 |
0,2880 |
0,6385 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8203 |
|
4 |
0,0345 |
0,1355 |
0,3004 |
0,5296 |
- |
- |
- |
- |
- |
- |
- |
0,8911 |
|
5 |
0,0189 |
0,0744 |
0,1648 |
0,2905 |
0,4514 |
- |
- |
- |
- |
- |
- |
0,9269 |
|
6 |
0,0116 |
0,0451 |
0,1000 |
0,1763 |
0,2740 |
0,3930 |
- |
- |
- |
- |
- |
0,9476 |
|
7 |
0,0075 |
0,0294 |
0,0652 |
0,1150 |
0,1787 |
0,2563 |
0,3479 |
- |
- |
- |
- |
0,9606 |
|
8 |
0,0052 |
0,0202 |
0,0449 |
0,0791 |
0,1229 |
0,1763 |
0,2394 |
0,3120 |
- |
- |
- |
0,9693 |
|
9 |
0,0037 |
0,0145 |
0,0322 |
0,0567 |
0,0882 |
0,1265 |
0,1717 |
0,2238 |
0,2827 |
- |
- |
0,9754 |
|
10 |
0,0028 |
0,0107 |
0,0239 |
0,0421 |
0,0654 |
0,0938 |
0,1273 |
0,1659 |
0,2097 |
0,2584 |
- |
0,9798 |
|
11 |
0,0024 |
0,0083 |
0,0183 |
0,0322 |
0,0498 |
0,0715 |
0,0971 |
0,1264 |
0,1598 |
0,1964 |
0,2378 |
0,9832 |
Таблица А.32 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения наибольшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
A |
|
2 |
-1,2500 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,3282 |
|
3 |
-1,1906 |
1,9535 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6518 |
|
4 |
-1,5183 |
-0,9909 |
1,8940 |
- |
- |
- |
- |
- |
- |
- |
0,7481 |
|
5 |
-1,5034 |
-0,9622 |
1,3919 |
2,9638 |
- |
- |
- |
- |
- |
- |
0,8235 |
|
6 |
-1,6852 |
-1,2811 |
-0,8475 |
1,3546 |
2,9291 |
- |
- |
- |
- |
- |
0,8639 |
|
7 |
-1,6788 |
-1,2709 |
-0,8295 |
1,1218 |
2,1591 |
3,7091 |
- |
- |
- |
- |
0,8936 |
|
8 |
-1,8007 |
-1,4582 |
-1,1326 |
-0,7516 |
1,0959 |
2,1361 |
3,6862 |
- |
- |
- |
0,9141 |
|
9 |
-1,7973 |
-1,4532 |
-1,1250 |
-0,7389 |
0,9564 |
1,7540 |
2,7510 |
4,3053 |
- |
- |
0,9288 |
|
10 |
-1,8872 |
-1,5826 |
-1,3102 |
-1,0262 |
-0,6814 |
0,9372 |
1,7374 |
2,7350 |
4,2891 |
- |
0,9408 |
|
11 |
-1,8851 |
-1,5796 |
-1,3061 |
-1,0204 |
-0,6717 |
0,8425 |
1,5010 |
2,2522 |
3,2414 |
4,8031 |
0,9490 |
Таблица А.33 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения наибольшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
А |
|
2 |
0,0305 |
0,9695 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,3282 |
|
3 |
0,0373 |
0,8305 |
0,1322 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6518 |
|
4 |
0,0104 |
0,0572 |
0,7927 - |
0,1397 |
- |
- |
- |
- |
- |
- |
- |
0,7481 |
|
5 |
0,0111 |
0,0619 |
0,7069 |
0,1698 |
0,0503 |
- |
- |
- |
- |
- |
- |
0,8235 |
|
6 |
0,0045 |
0,0228 |
0,0696 |
0,6756 |
0,1754 |
0,0521 |
- |
- |
- |
- |
- |
0,8639 |
|
7 |
0,0047 |
0,0236 |
0,0727 |
0,6210 |
0,1690 |
0,0848 |
0,0242 |
- |
- |
- |
- |
0,8936 |
|
8 |
0,0023 |
0,0112 |
0,0313 |
0,0751 |
0,5959 |
0,1727 |
0,0867 |
0,0248 |
- |
- |
- |
0,9141 |
|
9 |
0,0024 |
0,0115 |
0,0321 |
0,0773 |
0,5577 |
0,1601 |
0,0971 |
0,0484 |
0,0134 |
- |
- |
0,9288 |
|
10 |
0,0014 |
0,0063 |
0,0169 |
0,0369 |
0,0771 |
0,5374 |
0,1628 |
0,0985 |
0,0492 |
0,0136 |
- |
0,9408 |
|
11 |
0,0014 |
0,0064 |
0,0171 |
0,0374 |
0,0788 |
0,5089 |
0,1501 |
0,1000 |
0,0615 |
0,0302 |
0,0082 |
0,9490 |
Таблица А.34 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров распределения наибольшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
t 12 |
t 13 |
t 14 |
A |
|
3 |
-0,9581 |
1,2978 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4079 |
|
4 |
-1,2278 |
-0,335 |
1,5562 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5572 |
|
5 |
-1,3508 |
-0,6725 |
0,6688 |
2,2591 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6836 |
|
6 |
-1,4838 |
-0,9449 |
-0,2045 |
1,0080 |
2,5608 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7571 |
|
7 |
-1,5676 |
-1,096 |
-0,5419 |
0,3919 |
1,4614 |
2,9934 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8109 |
|
8 |
-1,6496 |
-1,2321 |
-0,7903 |
-0,1743 |
0,7262 |
1,7490 |
3,2777 |
- |
- |
- |
- |
- |
- |
- |
0,8480 |
|
9 |
-1,7097 |
-1,3265 |
-0,9444 |
-0,4717 |
0,2448 |
1,0698 |
2,0644 |
3,5952 |
- |
- |
- |
- |
- |
- |
0,8756 |
|
10 |
-1,7660 |
-1,4115 |
-1,0740 |
-0,6897 |
-0,1659 |
0,5499 |
1,3326 |
2,3149 |
3,8496 |
- |
- |
- |
- |
- |
0,8963 |
|
11 |
-1,8119 |
-1,4787 |
-1,1715 |
-0,8397 |
-0,4262 |
0,1576 |
0,5877 |
1,5877 |
2,5639 |
4,1040 |
- |
- |
- |
- |
0,9123 |
|
12 |
-1,8540 |
-1,5388 |
-1,2557 |
-0,9617 |
-0,619 |
-0,1648 |
0,4282 |
1,0689 |
1,8092 |
2,7833 |
4,3280 |
- |
- |
- |
0,9248 |
|
13 |
-1,8902 |
-1,5896 |
-1,3250 |
-1,0581 |
-0,7608 |
-0,3925 |
0,1020 |
0,6723 |
1,2894 |
2,0205 |
2,9948 |
4,5454 |
- |
- |
0,9349 |
|
14 |
-1,9234 |
-1,6354 |
-1,3862 |
-1,1406 |
-0,8763 |
-0,5658 |
-0,1654 |
0,3401 |
0,8852 |
1,4868 |
2,2126 |
3,1883 |
4,7419 |
- |
0,9431 |
|
15 |
-1,9531 |
-1,6757 |
-1,4391 |
-1,2101 |
-0,9701 |
-0,6990 |
-0,3665 |
0,0632 |
0,5564 |
1,0811 |
1,6723 |
2,3949 |
3,3713 |
4,9279 |
0,9498 |
Таблица А.35 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров распределения наибольшего экстремального значения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
P 12 |
P 13 |
P 14 |
P 15 |
A |
|
3 |
0,0738 |
0,6872 |
0,2390 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4079 |
|
4 |
0,0329 |
0,2142 |
0,5628 |
0,1901 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5572 |
|
5 |
0,0211 |
0,1199 |
0,4581 |
0,3018 |
0,0991 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6836 |
|
6 |
0,0122 |
0,0641 |
0,2169 |
0,4011 |
0,2314 |
0,0743 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7571 |
|
7 |
0,0083 |
0,0419 |
0,1290 |
0,3295 |
0,2843 |
0,1581 |
0,0489 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8109 |
|
8 |
0,0055 |
0,0269 |
0,0779 |
0,1938 |
0,3124 |
0,2238 |
0,1227 |
0,0370 |
- |
- |
- |
- |
- |
- |
- |
0,8480 |
|
9 |
0,0040 |
0,0191 |
0,0533 |
0,1250 |
0,2557 |
0,2525 |
0,1712 |
0,0921 |
0,0271 |
- |
- |
- |
- |
- |
- |
0,8756 |
|
10 |
0,0029 |
0,0136 |
0,0371 |
0,0827 |
0,1708 |
0,2545 |
0,2065 |
0,1379 |
0,0729 |
0,0211 |
- |
- |
- |
- |
- |
0,8963 |
|
11 |
0,0022 |
0,0102 |
0,0271 |
0,0589 |
0,1164 |
0,2101 |
0,2218 |
0,1683 |
0,1108 |
0,0578 |
0,0164 |
- |
- |
- |
- |
0,9123 |
|
12 |
0,0017 |
0,0078 |
0,0204 |
0,0432 |
0,0830 |
0,1515 |
0,2136 |
0,1882 |
0,1395 |
0,0912 |
0,0463 |
0,0131 |
- |
- |
- |
0,9248 |
|
13 |
0,0013 |
0,0061 |
0,0158 |
0,0329 |
0,0615 |
0,1099 |
0,1779 |
0,1947 |
0,1592 |
0,1165 |
0,0754 |
0,0383 |
0,0105 |
- |
- |
09349 |
|
14 |
0,0011 |
0,0048 |
0,0124 |
0,0255 |
0,0467 |
0,0814 |
0,1354 |
0,1836 |
0,1710 |
0,1357 |
0,0988 |
0,0632 |
0,0317 |
0,0087 |
- |
0,9431 |
|
15 |
0,0009 |
0,0039 |
0,0099 |
0,0203 |
0,0365 |
0,0623 |
0,1025 |
0,1548 |
0,1725 |
0,1486 |
0,1163 |
0,0842 |
0,0535 |
0,0266 |
0,0072 |
0,9498 |
Таблица А.36 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Коши) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
A |
|
2 |
-1,3274 1,3274 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,2867 0,2867 |
|
3 |
-1,0000 |
1,0000 |
- |
- |
- |
- |
- |
- |
- |
0,8106 |
|
4 |
-0,9597 -1,5797 |
0,7149 -0,7149 |
1,5797 0,9597 |
- - |
- - |
- - |
- - |
- - |
- - |
0,8630 0,8630 |
|
5 |
-1,5171 |
-0,6591 |
0,6591 |
1,5171 |
- |
- |
- |
- |
- |
0,9226 |
|
6 |
-1,4959 -1,9562 |
-0,6398 -1,0228 |
0,5438 -0,5438 |
1,0028 0,6398 |
1,9562 1,4959 |
- - |
- - |
- - |
- - |
0,9339 0,9339 |
|
7 |
-1,9269 |
-1,0000 |
-0,5190 |
0,5190 |
1,0000 |
1,9269 |
- |
- |
- |
0,9582 |
|
8 |
-1,9130 -2,2993 |
-0,9891 -1,2806 |
-0,5070 -0,8015 |
0,4529 -0,4529 |
0,8015 0,5070 |
1,2806 0,9801 |
2,2993 1,9130 |
- - |
- - |
0,9715 0,9715 |
|
9 |
-2,2814 |
-1,2674 |
-0,7891 |
-0,4384 |
0,4384 |
0,7891 |
1,2674 |
2,2814 |
- |
0,9739 |
|
10 |
-2,2712 -2,6124 |
-1,2600 -1,5060 |
-0,7819 -1,0078 |
-0,4300 -0,6579 |
0,3944 -0,3944 |
0,6759 0,4300 |
1,0078 0,7819 |
1,5060 1,2600 |
2,6124 2,2712 |
0,9780 0,9780 |
|
11 |
-2,6002 |
-1,4972 |
-1,0000 |
-0,6679 |
-0,3846 |
0,6679 |
1,0000 |
1,4972 |
2,6002 |
0,9821 |
Таблица А.37 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Коши) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
A |
|
2 |
0,2055 |
0,7945 |
- |
- |
- |
_ |
- |
- |
- |
- |
- |
0,2867 |
|
3 |
0,7945 0,2500 |
0,2055 0,5000 |
- 0,2500 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,2867 0,8106 |
|
4 |
0,2565 0,1796 |
0,4411 0,1228 |
0,1228 0,4411 |
0,1796 0,2565 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,8630 0,8630 |
|
5 |
0,1855 |
0,1290 |
0,3710 |
0,1290 |
0,1855 |
- |
- |
- |
- |
- |
- |
0,9226 |
|
6 |
0,1876 0,1504 |
0,1312 0,0960 |
0,3397 0,0951 |
0,0951 0,3397 |
0,0960 0,1312 |
0,1504 0,1876 |
- - |
- - |
- - |
- - |
- - |
0,9339 0,9339 |
|
7 |
0,1524 |
0,0976 |
0,0976 |
0,3048 |
0,0976 |
0,0976 |
0,1524 |
- |
- |
- |
- |
0,9583 |
|
8 |
0,1533 0,1306 |
0,0984 0,0804 |
0,0989 0,0739 |
0,2848 0,7978 |
0,0797 0,2848 |
0,0739 0,0989 |
0,0804 0,0984 |
0,1306 0,1533 |
- - |
- - |
- - |
0,9715 0,9715 |
|
9 |
0,1315 |
0.0811 |
0,0748 |
0,0811 |
0,2630 |
0,0811 |
0,0748 |
0,0811 |
0,1315 |
- |
- |
0,9739 |
|
10 |
0,1320 0,1164 |
0,0815 0,0702 |
0,0753 0,0622 |
0,0819 0,0620 |
0,2489 0,0696 |
0,0696 0,2489 |
0,0620 0,0819 |
0,0622 0,0753 |
0,0702 0,0815 |
0,1164 0,1320 |
- - |
0,9780 0,9780 |
|
11 |
0,1169 |
0,0705 |
0,0626 |
0,0626 |
0,0705 |
0,2338 |
0,0705 |
0,0626 |
0,0626 |
0,0705 |
0,1169 |
0,9821 |
Таблица А.38 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании параметра сдвига распределения Коши) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
A |
|
2 |
0,0 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,8106 |
|
3 |
-0,1794 |
0,1794 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,8577 |
|
4 |
-3,2845 -0,1570 |
-0,2390 0,2390 |
0,1570 3,2845 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,8991 0,8991 |
|
5 |
-3,3338 |
-0,2137 |
0,2137 |
3,3338 |
- |
- |
- |
- |
- |
- |
- |
0,9393 |
|
6 |
-3,1577 |
-0,3168 |
0,0 |
0,3168 |
0,1577 |
- |
- |
- |
- |
- |
- |
0,9582 |
|
7 |
-3,0827 |
-0,3786 |
-0,1150 |
0,1150 |
0,3786 |
3,0827 |
- |
- |
- |
- |
- |
0,9658 |
|
8 |
-5,0956 -3,0863 |
-2,2911 0,3744 |
-0,4018 -0,1072 |
-0,1275 0,1275 |
0,1072 0,4018 |
0,3744 2,2911 |
3,0863 5,0965 |
- - |
- - |
- - |
- - |
0,9718 0,9718 |
|
9 |
-5,1041 |
-2,2961 |
-0,3972 |
-0,1196 |
0,1196 |
0,3972 |
2,2961 |
5,1041 |
- |
- |
- |
0,9779 |
|
10 |
-5,0213 |
-2,2496 |
-0,4445 |
-0,1991 |
0,0 |
0,1991 |
0,4445 |
0,4445 |
2,2496 |
5,0213 |
- |
0,9821 |
|
11 |
-4,9723 |
-2,2216 |
-0,4792 |
-0,2572 |
-0,0820 |
0,0820 |
0,2572 |
0,4792 |
2,2216 |
4,9723 |
- |
0,9845 |
|
12 |
-4,9357 |
-2,2027 |
-0,5059 |
-0,3020 |
-0,1433 |
0,0 |
0,1433 |
0,3020 |
0,5059 |
2,2027 |
4,9357 |
0,9860 |
Таблица А.39 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании параметра сдвига распределения Коши) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
P 12 |
А |
|
2 |
0,5 |
0,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,8106 |
|
3 |
0,4435 |
0,1130 |
0,4435 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,8577 |
|
4 |
0,0941 0,4504 |
0,3312 0,1243 |
0,1243 0,3312 |
0,4504 0,0941 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,8991 0,8991 |
|
5 |
0,0928 |
0,3402 |
0,1340 |
0,3402 |
0,0928 |
- |
- |
- |
- |
- |
- |
- |
0,9393 |
|
6 |
0,0976 |
0,3047 |
0,0977 |
0,0977 |
0,3047 |
0,0976 |
- |
- |
- |
- |
- |
- |
0,9582 |
|
7 |
0,0998 |
02850 |
0,0788 |
0,0728 |
0,0788 |
0,2850 |
0,0998 |
- |
- |
- |
- |
- |
0,9658 |
|
8 |
0,0617 0,0997 |
0,0693 0,2863 |
0,2474 0,0800 |
0,0812 0,0744 |
0,0744 0,0812 |
0,0800 0,2474 |
0,2863 0,0693 |
0,0997 0,0617 |
- - |
- - |
- - |
- - |
0,9718 0,9718 |
|
9 |
0,0616 |
0,0691 |
0,2490 |
0,0824 |
0,0758 |
0,0824 |
0,2490 |
0,0691 |
0,0616 |
- |
- |
- |
0,9779 |
|
10 |
0,0626 |
0,0705 |
0,2338 |
0,0705 |
0,0626 |
0,0626 |
0,0705 |
0,2338 |
0,0705 |
0,0626 |
- |
- |
0,9821 |
|
11 |
0,0632 |
0,0714 |
0,2232 |
0,0621 |
0,0541 |
0,0520 |
0,0541 |
0,0621 |
0,2232 |
0,0714 |
0,0632 |
- |
0,9845 |
|
12 |
0,0636 |
0,0721 |
0,2152 |
0,0557 |
0,0481 |
0,0453 |
0,0453 |
0,0481 |
0,0557 |
0,2152 |
0,0721 |
0,0636 |
0,9860 |
Таблица А.40 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров распределения Коши) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
t 12 |
t 13 |
t 14 |
A |
|
3 |
-0,5773 |
0,5773 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4677 |
|
4 |
-1,0000 |
0,0 |
1,0000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6570 |
|
5 |
-1,3764 |
-0,3249 |
0,3249 |
1,3764 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7659 |
|
6 |
-1,7320 |
-0,5773 |
0,0 |
0,5773 |
1,7320 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,8315 |
|
7 |
-2,0765 |
-0,7975 |
-0,2282 |
0,2282 |
0,7975 |
2,0765 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8735 |
|
8 |
-2,4142 |
-1,0000 |
-0,4142 |
0,0 |
0,4142 |
1,0000 |
2,4142 |
- |
- |
- |
- |
- |
- |
- |
0,9018 |
|
9 |
-2,7475 |
-1,1917 |
-0,5773 |
-0,1763 |
0,1763 |
0,5773 |
1,1917 |
2,7475 |
- |
- |
- |
- |
- |
- |
0,9217 |
|
10 |
-3,0778 |
-1,3764 |
-0,7266 |
-0,3249 |
0,0 |
0,3249 |
0,7266 |
1,3764 |
3,0778 |
- |
- |
- |
- |
- |
0,9361 |
|
11 |
-3,4062 |
-1,5561 |
-0,8665 |
-0,4567 |
-0,1438 |
0,1438 |
0,4567 |
0,8665 |
1,5561 |
3,4062 |
- |
- |
- |
- |
0,9469 |
|
12 |
-3,7319 |
-1,7320 |
-1,0000 |
-0,5773 |
-0,2679 |
0,0 |
0,2679 |
0,5773 |
1,0000 |
1,7320 |
3,7319 |
- |
- |
- |
0,9552 |
|
13 |
-4,0573 |
-1,9053 |
-1,1288 |
-0,6903 |
-0,3793 |
-0,1214 |
0,1214 |
0,3793 |
0,6903 |
1,1288 |
1,9053 |
4,0573 |
- |
- |
0,9617 |
|
14 |
-4,3809 |
-2,0763 |
-1,2538 |
-0,7974 |
-0,4815 |
-0,2282 |
0,0 |
0,2282 |
0,4815 |
0,7974 |
1,2538 |
2,0763 |
4,3809 |
- |
0,9669 |
|
15 |
-4,7041 |
-2,2457 |
-1,3762 |
-0,9030 |
-0,5773 |
-0,3249 |
-0,1051 |
0,1051 |
0,3249 |
0,5773 |
0,9003 |
1,3762 |
2,2457 |
4,7041 |
0,9711 |
Таблица А.41 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании параметра сдвига логистического распределения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
A |
|
2 |
0,0 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7500 |
|
3 |
-0,6931 |
0,6931 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8889 |
|
4 |
-1,0986 |
0,0 |
1,0986 |
- |
- |
- |
- |
- |
- |
- |
0,9375 |
|
5 |
-1,3863 |
-0,4055 |
0,4055 |
1,3863 |
- |
- |
- |
- |
- |
- |
0,9600 |
|
6 |
-1,6094 |
-0,6931 |
0,0 |
0,6931 |
1,6094 |
- |
- |
- |
- |
- |
0,9722 |
|
7 |
-1,7918 |
-0,9163 |
-0,2877 |
0,2877 |
0,9163 |
1,7918 |
- |
- |
- |
- |
0,9796 |
|
8 |
-1,9459 |
-1,0986 |
-0,5108 |
0,0 |
0,5108 |
1,0986 |
1,9459 |
- |
- |
- |
0,9844 |
|
9 |
-2,0794 |
-1,2528 |
-0,6931 |
-0,2231 |
0,2231 |
0,6931 |
1,2528 |
2,0794 |
- |
- |
0,9876 |
|
10 |
-2,1972 |
-1,3863 |
-0,8473 |
-0,4055 |
0,0 |
0,4055 |
0,8473 |
1,3863 |
2,1972 |
- |
0,9900 |
|
11 |
-2,3026 |
-1,5041 |
-0,9808 |
-0,5596 |
-0,1823 |
0,1823 |
0,5596 |
0,9808 |
1,5041 |
2,3026 |
0,9921 |
Таблица А.42 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра логистического распределения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
A |
|
2 |
-2,3993 2,3993 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,3074 0,3074 |
|
3 |
-2,1651 |
2,1651 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6804 |
|
4 |
-3,2424 -2,1049 |
-1,6762 1,6267 |
2,1049 3,2424 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,7618 0,7618 |
|
5 |
-3,1685 |
-1,5929 |
1,5929 |
3,1385 |
- |
- |
~ |
- |
- |
- |
0,8449 |
|
6 |
-3,9427 3,1638 |
-2,4141 -1,5566 |
-1,3564 1,3564 |
1,5566 2,4141 |
3,1368 3,9427 |
- - |
- - |
- - |
- - |
- - |
0,8757 0,8757 |
|
7 |
-3,9053 |
-2,3760 |
-1,3107 |
1,3107 |
2,3760 |
3,9053 |
- |
- |
- |
- |
0,9078 |
|
8 |
-4,5191 -3,8845 |
-2,9874 -2,3552 |
-1,9953 -1,2866 |
-1,1639 1,1639 |
1,2856 1,9953 |
2,3552 2,9874 |
3,8845 4,5191 |
- - |
- - |
- - |
0,9233 0,9233 |
|
9 |
-4,4961 |
-2,9648 |
-1,9713 |
-1,1341 |
1,1341 |
1,9713 |
2,9648 |
4,4961 |
- |
- |
0,9391 |
|
10 |
-4,4819 -5,0067 |
-2,9508 -3,4650 |
-1,9565 -2,4887 |
-1,1156 -1,7314 |
1,0318 -1,0318 |
1,7314 1,1156 |
2,4887 1,9565 |
3,4650 2,9508 |
5,0067 4,4819 |
- - |
0,9478 0,9478 |
|
11 |
-4,9907 |
-3,4496 |
-2,4733 |
-1,7145 |
-1,0104 |
1,0104 |
1,7145 |
2,4733 |
3,4496 |
4,9907 |
0,9568 |
Таблица А.43 - Оптимальные вероятности (частоты) при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра логистического распределения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
А |
|
2 |
0,0832 0,9168 |
0,9168 0,0832 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,3074 0,3074 |
|
3 |
0,1029 |
0,7942 |
0,1029 |
- |
- |
- |
- |
- |
- |
- |
- |
0,6844 |
|
4 |
0,0376 0,1086 |
0,1200 0,7338 |
0,7338 0,1200 |
0,1086 0,0376 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,7618 0,7618 |
|
5 |
0,0404 |
0,1286 |
0,6620 |
0,1286 |
0,0404 |
- |
- |
- |
- |
- |
- |
0,8449 |
|
6 |
0,0190 0,0416 |
0,0631 0,1325 |
0,1227 0,6211 |
0,6211 0,1227 |
0,1325 0,0631 |
0,0416 0,0190 |
- - |
- - |
- - |
- - |
- - |
0,8757 0,8757 |
|
7 |
0,0197 |
0,0653 |
0,1274 |
0,5752 |
0,1274 |
0,0653 |
0,0197 |
- |
- |
- |
- |
0,9078 |
|
8 |
0,0108 0,0201 |
0,0372 0,0666 |
0,0717 0,1299 |
0,1183 0,5454 |
0,5454 0,1183 |
0,1299 0,0717 |
0,0666 0,0372 |
0,0201 0,0108 |
- - |
- - |
- - |
0,9233 0,9233 |
|
9 |
0,0110 |
0,0380 |
0,0732 |
0,1212 |
0,5132 |
0.1212 |
0,0732 |
0,0380 |
0,0110 |
- |
- |
0,9391 |
|
10 |
0,0066 0,0112 |
0,0237 0,0385 |
0,0464 0,0741 |
0,0737 0,1239 |
0,1123 0,4905 |
0,4905 0,1123 |
0,1230 0,0737 |
0,0741 0,0464 |
0,0385 0,0237 |
0,0112 0,0066 |
- - |
0,9478 0,9478 |
|
11 |
0,0068 |
0,0240 |
0,0470 |
0,0748 |
0,1143 |
0,4662 |
0,1143 |
0,0748 |
0,0470 |
0,0240 |
0,0068 |
0,9568 |
Таблица А.44 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров логистического распределения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
t 12 |
t 13 |
t 14 |
A |
|
3 |
-1,1674 |
1,1674 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4426 |
|
4 |
-1,9797 |
0,0 |
1,9797 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6026 |
|
5 |
-2,5090 |
-0,8470 |
0,8470 |
2,5090 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6861 |
|
6 |
-2,9083 |
-1,3335 |
0,0 |
1,3335 |
2,9083 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7890 |
|
7 |
-3,2797 |
-1,7426 |
-0,5955 |
0,5955 |
1,7426 |
3,2797 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8369 |
|
8 |
-3,6023 |
-2,0786 |
-1,0165 |
0,0 |
1,0165 |
2,0786 |
3,6023 |
- |
- |
- |
- |
- |
- |
- |
0,8701 |
|
9 |
-3,8981 |
-2,3777 |
-1,3604 |
-0,4631 |
0,4631 |
1,3604 |
2,3777 |
3,8981 |
- |
- |
- |
- |
- |
- |
0,8942 |
|
10 |
-4,1665 |
-2,6442 |
-1,6512 |
-0,8235 |
0,0 |
0,8235 |
1,6512 |
2,6442 |
4,1665 |
- |
- |
- |
- |
- |
0,9123 |
|
11 |
-4,4148 |
-2,8883 |
-1,9085 |
-1,1227 |
-0,3805 |
0,3805 |
1,1227 |
1,9085 |
2,8883 |
4,4148 |
- |
- |
- |
- |
0,9261 |
|
12 |
-4,6437 |
-3,1123 |
-2,1394 |
-1,3798 |
-0,6929 |
0,0 |
0,6929 |
1,3798 |
2,1394 |
3,1123 |
4,6437 |
- |
- |
- |
0,9371 |
|
13 |
-4,8577 |
-3,3212 |
-2,3511 |
-1,6081 |
-0,9580 |
-0,3225 |
0,3235 |
0,9580 |
1,6081 |
2,3511 |
3,3212 |
4,8577 |
- |
- |
0,9457 |
|
14 |
-5,0564 |
-3,5150 |
-2,5460 |
-1,8138 |
-1,1888 |
-0,5984 |
0,0 |
0,5984 |
1,1888 |
1,8138 |
2,5460 |
3,5150 |
5,0564 |
- |
0,9526 |
|
15 |
-5,2452 |
-3,6987 |
-2,7289 |
-2,0032 |
-1,3953 |
-0,8364 |
-0,2818 |
0,2818 |
0,8364 |
1,3953 |
2,0032 |
2,4289 |
3,6987 |
5,2452 |
0,9585 |
Таблица А.45 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров логистического распределения) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
P 11 |
P 12 |
P 13 |
P 14 |
P 15 |
A |
|
3 |
0,2373 |
0,5254 |
0,2373 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4426 |
|
4 |
0,1214 |
0,3786 |
0,3786 |
0,1214 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6026 |
|
5 |
0,0752 |
0,2249 |
0,3998 |
0,2249 |
0,0752 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6861 |
|
6 |
0,0517 |
0,1568 |
0,2915 |
0,2915 |
0,1568 |
0,0517 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7890 |
|
7 |
0,0363 |
0,1127 |
0,2064 |
0,2892 |
0,2064 |
0,1127 |
0,0363 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8369 |
|
8 |
0,0265 |
0,0847 |
0,1545 |
0,2343 |
0,2343 |
0,1545 |
0,0847 |
0,0265 |
- |
- |
- |
- |
- |
- |
- |
0,8701 |
|
9 |
0,0199 |
0,0650 |
0,1193 |
0,1821 |
0,2274 |
0,1821 |
0,1193 |
0,0650 |
0,0199 |
- |
- |
- |
- |
- |
- |
0,8942 |
|
10 |
0,0153 |
0,0510 |
0,0946 |
0,1441 |
0,1950 |
0,1950 |
0,1441 |
0,0946 |
0,0510 |
0,0153 |
- |
- |
- |
- |
- |
0,9123 |
|
11 |
0,0119 |
0,0408 |
0,0764 |
0,1164 |
0,1605 |
0,1880 |
0,1605 |
0,1164 |
0,0764 |
0,0408 |
0,0119 |
- |
- |
- |
- |
0,9261 |
|
12 |
0,0095 |
0,0331 |
0,0627 |
0,0957 |
0,1324 |
0,1666 |
0,1666 |
0,1324 |
0,0957 |
0,0627 |
0,0331 |
0,0095 |
- |
- |
- |
0,9371 |
|
13 |
0,0077 |
0,0271 |
0,0521 |
0,0799 |
0,1104 |
0,1425 |
0,1606 |
0,1425 |
0,1104 |
0,0799 |
0,0521 |
0,0271 |
0,0077 |
- |
- |
0,9457 |
|
14 |
0,0063 |
0,0226 |
0,0438 |
0,0675 |
0,0933 |
0,1212 |
0,1453 |
0,1453 |
0,1212 |
0,0933 |
0,0675 |
0,0438 |
0,0226 |
0,0063 |
- |
0,9526 |
|
15 |
0,0053 |
0,0189 |
0,0371 |
0,0576 |
0,0797 |
0,1037 |
0,1277 |
0,1400 |
0,1277 |
0,1037 |
0,0797 |
0,0576 |
0,0371 |
0,0189 |
0,0053 |
0,9585 |
Таблица А.46 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Лапласа) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
А |
|
2 |
1,8416 -1,8416 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,2920 0,2920 |
|
3 |
-1,5936 |
1,5936 |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
4 |
-2,7044 -1,5183 |
-1,1121 1,1121 |
1,5183 2,7044 |
- - |
- - |
- - |
- - |
- - |
- - |
0,7303 0,7303 |
|
5 |
-2,6112 |
-1,0176 |
1,0176 |
2,6112 |
- |
- |
- |
- |
- |
0,8203 |
|
6 |
-2,5670 -3,4173 |
-0,9745 -1,8233 |
0,8045 -0,8045 |
1,8233 0,9745 |
3,4173 2,5670 |
- - |
- - |
- - |
- - |
0,8548 0,8548 |
|
7 |
-3,3652 |
-1,7716 |
-0,7544 |
0,7544 |
1,7716 |
3,3652 |
- |
- |
- |
0,8910 |
|
8 |
-3,3329 -3,9879 |
-1,7388 -2,3972 |
-0,7266 -1,3816 |
0,6311 -0,6311 |
1,3816 0,7266 |
2,3972 1,7388 |
3,9879 3,3329 |
- - |
- - |
0,9087 0,9087 |
|
9 |
-3,9657 |
-2,3720 |
-1,3545 |
-0,6004 |
0,6004 |
1,3545 |
2,3720 |
3,9657 |
- |
0,9269 |
|
10 |
-3,9468 -4,5228 |
-2,3487 -2,9054 |
-1,3335 -1,8811 |
-0,5817 -1,1246 |
0,5217 -0,5217 |
1,1246 0,5817 |
1,8811 1,3335 |
2,9054 2,3487 |
4,5228 3,9468 |
0,9371 0,9371 |
Таблица А.47 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Лапласа) и соответствующие значения относительной асимптотической информации А
|
k |
± t 1 |
± t 2 |
± t 3 |
± t 4 |
± t 5 |
± t 6 |
± t 7 |
± t 8 |
± t 9 |
А |
|
11 |
±0,4993 |
±1,0997 |
±1,8538 |
±2,8714 |
±4,4650 |
- |
- |
- |
- |
0,9476 |
|
13 |
±0,4276 |
±0,9269 |
±1,5273 |
±2,2813 |
±3,2989 |
±4,8925 |
- |
- |
- |
0,9606 |
|
15 |
±0,3739 |
±0,8015 |
±1,3008 |
±1,9012 |
±2,6553 |
±3,6729 |
±5,2665 |
- |
- |
0,9693 |
|
17 |
±0,3323 |
±0,7063 |
±1,1338 |
±1,6331 |
±2,2336 |
±2,9876 |
±4,0052 |
±5,5988 |
- |
0,9754 |
|
19 |
±0,2990 |
±0,6314 |
±1,0053 |
±1,4329 |
±1,9322 |
±2,5326 |
±3,2866 |
±4,3042 |
±5,8979 |
0,9798 |
|
Примечание - Граничные точки интервалов симметричны относительно нуля. |
||||||||||
Таблица А.48 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Лапласа) и соответствующие значения относительной асимптотической информации А
|
k |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
P 10 |
А |
|
2 |
0,9207 0,0793 |
0,0793 0,9207 |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
- - |
0,2920 0,2920 |
|
3 |
0,1016 |
0,7968 |
0,1016 |
- |
- |
- |
- |
- |
- |
- |
0,6476 |
|
4 |
0,0335 0,1095 |
0,1310 0,7260 |
0,7260 0,1310 |
0,1095 0,0335 |
- - |
- - |
- - |
- - |
- - |
- - |
0,7303 0,7303 |
|
5 |
0,0367 |
0,1440 |
0,6386 |
0,1440 |
0,0367 |
- |
- |
_ |
_ |
__ |
0,8203 |
|
6 |
0,0384 0,0164 |
0,1503 0,0643 |
0,5877 0,1429 |
0,1429 0,5877 |
0,0643 0,1503 |
0,0164 0,0384 |
- - |
- - |
- - |
- - |
0,8548 0,8548 |
|
7 |
0,0173 |
0,0677 |
0,1502 |
0,5296 |
0,1502 |
0,0677 |
0,0173 |
- |
- |
- |
0,8910 |
|
8 |
0,0179 0,0093 |
0,0700 0,0362 |
0,1539 0,0801 |
0,4922 0,1404 |
0,1404 0,4922 |
0,0801 0,1593 |
0,0362 0,0700 |
0,0093 0,0178 |
- - |
- - |
0,9087 0,9087 |
|
9 |
0,0094 |
0,0372 |
0,0824 |
0,1453 |
0,4514 |
0,1453 |
0,0824 |
0,0372 |
0,0094 |
- |
0,9269 |
|
10 |
0,0097 0,0054 |
0,0381 0,0219 |
0,0840 0,0488 |
0,1477 0,0862 |
0,4238 0,1344 |
0,1344 0,4328 |
0,0862 0,1477 |
0,0488 0,0840 |
0,0219 0,0381 |
0,0054 0,0096 |
0,9371 0,9371 |
Таблица А.49 - Оптимальные вероятности (частоты) при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра распределения Лапласа) и соответствующие значения относительной асимптотической информации А
|
k |
P 0 |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
P 9 |
А |
|
11 |
0,3930 |
0,1370 |
0,0882 |
0,0500 |
0,0225 |
0,0058 |
- |
- |
- |
- |
0,9476 |
|
13 |
0,3478 |
0,1282 |
0,0894 |
0,0575 |
0,0326 |
0,0147 |
0,0037 |
- |
- |
- |
0,9606 |
|
15 |
0,3120 |
0,1197 |
0,0882 |
0,0614 |
0,0396 |
0,0224 |
0,0101 |
0,0026 |
- |
- |
0,9693 |
|
17 |
0,2826 |
0,1119 |
0,0859 |
0,0633 |
0,0441 |
0,0283 |
0,0161 |
0,0073 |
0,0018 |
- |
0,9754 |
|
19 |
0,2584 |
0,1049 |
0,0829 |
0,0637 |
0,0469 |
0,0327 |
0,0210 |
0,0119 |
0,0054 |
0,0014 |
0,9798 |
|
Примечание - В таблице приведены значения вероятностей попадания наблюдений в центральный интервал P 0 интервалы правее центра: Р 1 , P 2 , . . . Значения вероятностей попадания в интервалы левее центра получаются зеркальным отражением. |
|||||||||||
Таблица А.50 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра двойного показательного распределения) и соответствующие значения относительной асимптотической информации А
|
k |
ti |
θ2 |
||||||||||
|
0,5 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
2 |
t 1 |
5,9243 |
3,4910 |
0,1058 |
0,0952 |
0,0864 |
0,0792 |
0,0730 |
0,0679 |
0,0634 |
00594 |
0,0560 |
|
|
А |
0,5239 |
0,3283 |
0,5580 |
0,6494 |
0,6742 |
0,6798 |
0,6795 |
0,6774 |
0,6750 |
0,6725 |
0,6702 |
|
3 |
t 1 |
5,7236 |
3,2901 |
0,1714 |
0,1578 |
0,1458 |
0,1353 |
0,1260 |
0,1178 |
0,1106 |
0,1042 |
0,0984 |
|
|
t 2 |
0,1704 |
0,1417 |
0,0371 |
0,0351 |
0,0330 |
0,0312 |
0,0295 |
0,0279 |
0,0265 |
0,0253 |
0,0242 |
|
|
А |
0,6465 |
0,6518 |
0,6790 |
0,7947 |
0,8286 |
0,8384 |
0,8404 |
0,8397 |
0,8382 |
0,8365 |
0,8348 |
|
4 |
t 1 |
8,2073 |
4,5218 |
1,9539 |
0,1979 |
0,1851 |
0,1737 |
0,1630 |
0,1535 |
0,1447 |
0,1369 |
0,1296 |
|
|
t 2 |
4,5709 |
2,6958 |
0,1871 |
0,0737 |
0,0694 |
0,0656 |
0,0620 |
0,0588 |
0,0558 |
0,0530 |
0,0506 |
|
|
t 3 |
0,1986 |
0,1504 |
0,0404 |
0,0166 |
0,0161 |
0,0155 |
0,0149 |
0,0143 |
0,0138 |
0,0133 |
0,0128 |
|
|
А |
0,7910 |
0,7481 |
0,8049 |
0,8497 |
0,8879 |
0,8999 |
0,9033 |
0,9036 |
0,9029 |
0,9018 |
0,9006 |
|
5 |
t 1 |
9,9575 |
4,5027 |
1,9227 |
1,4712 |
0,2135 |
0,2012 |
0,1906 |
0,1799 |
0,1709 |
0,1617 |
0,1540 |
|
|
t 2 |
6,4293 |
2,6201 |
0,2361 |
0,2097 |
0,1002 |
0,0950 |
0,0898 |
0,0851 |
0,0810 |
0,0770 |
0,0734 |
|
|
t 3 |
3,9668 |
0,2484 |
0,0860 |
0,0772 |
0,0393 |
0,0378 |
0,0362 |
0,0346 |
0,0331 |
0,0318 |
0,0305 |
|
|
t 4 |
0,2096 |
0,0518 |
0,0189 |
0,0174 |
0,0089 |
0,0088 |
0,0085 |
0,0083 |
0,0081 |
0,0078 |
0,0076 |
|
|
A |
0,8484 |
0,8235 |
0,8546 |
0,8919 |
0,9167 |
0,9300 |
0,9343 |
0,9353 |
0,9351 |
0,9344 |
0,9336 |
|
6 |
t 1 |
9,8965 |
5,3402 |
2,5662 |
1,4602 |
0,2346 |
0,2231 |
0,2118 |
0,2007 |
0,1916 |
0,1825 |
0,1738 |
|
|
t 2 |
6,3520 |
3,5979 |
1,6106 |
0,2410 |
0,1257 |
0,1192 |
0,1131 |
0,1071 |
0,1025 |
0,0977 |
0,0931 |
|
|
t 3 |
3,8701 |
2,3295 |
0,2457 |
0,1114 |
0,0622 |
0,0596 |
0,0567 |
0,0540 |
0,0522 |
0,0498 |
0,0476 |
|
|
t 4 |
0,3459 |
0,2582 |
0,0889 |
0,0429 |
0,0245 |
0,0238 |
0,0230 |
0,0221 |
0,0216 |
0,0208 |
0,0199 |
|
|
t 5 |
0,0699 |
0,0533 |
0,0195 |
0,0095 |
0,0055 |
0,0054 |
0,0053 |
0,0051 |
0,0051 |
0,0050 |
0,0048 |
|
|
A |
0,8799 |
0,8639 |
0,8891 |
0,9200 |
0,9328 |
0,9469 |
0,9518 |
0,9533 |
0,9534 |
0,9530 |
0,9525 |
|
7 |
t 1 |
11,2128 |
5,3662 |
2,5559 |
1,4460 |
1,2202 |
0,2395 |
0,2292 |
0,2182 |
0,2082 |
0,1988 |
0,1904 |
|
|
t 2 |
7,7564 |
3,5651 |
1,5897 |
0,2642 |
0,2443 |
0,1394 |
0,1332 |
0,1264 |
0,1206 |
0,1150 |
0,1103 |
|
|
t 3 |
5,4226 |
2,2911 |
0,2825 |
0,1393 |
0,1297 |
0,0792 |
0,0762 |
0,0723 |
0,0693 |
0,0662 |
0,0637 |
|
|
t 4 |
3,5152 |
0,3265 |
0,1295 |
0,0676 |
0,0639 |
0,0402 |
0,0391 |
0,0373 |
0,0359 |
0,0345 |
0,0334 |
|
|
t 5 |
0,3610 |
0,1156 |
0,0489 |
0,0260 |
0,0252 |
0,0160 |
0,0158 |
0,0152 |
0,0147 |
0,0142 |
0,0139 |
|
|
t 6 |
0,0727 |
0,0245 |
0,0106 |
0,0057 |
0,0056 |
0,0035 |
0,0035 |
0,0035 |
0,0034 |
0,0033 |
0,0032 |
|
|
A |
0,9094 |
0,8935 |
0,9141 |
0,9357 |
0,9493 |
0,9574 |
0,9626 |
0,9644 |
0,9648 |
0,9647 |
0,9643 |
|
8 |
t 1 |
12,4184 |
6,0434 |
2,9963 |
1,8917 |
1,2107 |
0,2534 |
0,2425 |
0,2324 |
0,2216 |
0,2134 |
0,2039 |
|
|
t 2 |
8,9812 |
4,2908 |
2,0838 |
1,2386 |
0,2631 |
0,1575 |
0,1495 |
0,1431 |
0,1359 |
0,1307 |
0,1248 |
|
|
t 3 |
6,6955 |
3,0976 |
1,4411 |
0,2722 |
0,1517 |
0,0974 |
0,0926 |
0,0892 |
0,0843 |
0,0815 |
0,0778 |
|
|
t 4 |
4,8980 |
2,1156 |
0,2887 |
0,1435 |
0,0851 |
0,0565 |
0,0540 |
0,0524 |
0,0495 |
0,0482 |
0,0462 |
|
|
t 5 |
3,3170 |
0,3342 |
0,1321 |
0,0701 |
0,0426 |
0,0287 |
0,0278 |
0,0272 |
0,0257 |
0,0252 |
0,0244 |
|
|
t 6 |
0,3690 |
0,1175 |
0,0499 |
0,0272 |
0,0167 |
0,0113 |
0,0111 |
0,0109 |
0,0104 |
0,0103 |
0,0101 |
|
|
t 7 |
0,0743 |
0,0249 |
0,0109 |
0,0060 |
0,0036 |
0,0025 |
0,0024 |
0,0024 |
0,0023 |
0,0023 |
0,0023 |
|
|
A |
0,9261 |
0,9141 |
0,9283 |
0,9477 |
0,9596 |
0,9643 |
0,9698 |
0,9718 |
0,9724 |
0,9724 |
0,9721 |
|
9 |
t 1 |
12,2869 |
6,0573 |
2,9859 |
1,8703 |
1,2022 |
1,0648 |
0,2549 |
0,2449 |
0,2349 |
0,2255 |
0,2148 |
|
|
t 2 |
8,8417 |
4,2945 |
2,0795 |
1,2237 |
0,2765 |
0,2619 |
0,1654 |
0,1574 |
0,1508 |
0,1444 |
0,1370 |
|
|
t 3 |
6,5618 |
3,0962 |
1,4280 |
0,2939 |
0,1697 |
0,1608 |
0,1087 |
0,1037 |
0,0991 |
0,0949 |
0,0897 |
|
|
t 4 |
4,7832 |
2,1001 |
0,3166 |
0,1693 |
0,1038 |
0,0987 |
0,0692 |
0,0661 |
0,0634 |
0,0609 |
0,0574 |
|
|
t 5 |
3,2276 |
0,3840 |
0,1652 |
0,0946 |
0,0593 |
0,0569 |
0,0408 |
0,0391 |
0,0377 |
0,0364 |
0,0343 |
|
|
t 6 |
0,4694 |
0,1733 |
0,0795 |
0,0467 |
0,0296 |
0,0287 |
0,0208 |
0,0202 |
0,0197 |
0,0190 |
0,0180 |
|
|
t 7 |
0,1633 |
0,0642 |
0,0302 |
0,0181 |
0,0114 |
0,0113 |
0,0082 |
0,0080 |
0,0079 |
0,0077 |
0,0073 |
|
|
t 8 |
0,0340 |
0,0136 |
0,0064 |
0,0039 |
0,0025 |
0,0024 |
0,0018 |
0,0018 |
0,0017 |
0,0017 |
0,0016 |
|
|
A |
0,9387 |
0,9288 |
0,9425 |
0,9577 |
0,9664 |
0,9713 |
0,9748 |
0,9770 |
0,9777 |
0,978 |
0,9777 |
|
10 |
t 1 |
13,2458 |
6,6629 |
2,9794 |
1,8704 |
1,1963 |
1,0539 |
0,2636 |
0,2536 |
0,2457 |
0,2350 |
0,2258 |
|
|
t 2 |
9,8558 |
4,9268 |
2,0697 |
1,2180 |
0,2912 |
0,2787 |
0,1769 |
0,1688 |
0,1637 |
0,1554 |
0,1491 |
|
|
t 3 |
7,6321 |
3,7589 |
1,4116 |
0,3107 |
0,1888 |
0,1807 |
0,1220 |
0,1160 |
0,1127 |
0,1066 |
0,1021 |
|
|
t 4 |
5,8941 |
2,8248 |
0,3426 |
0,1908 |
0,1234 |
0,1185 |
0,0826 |
0,0785 |
0,0766 |
0,0722 |
0,0693 |
|
|
t 5 |
4,4362 |
1,9905 |
0,1972 |
0,1164 |
0,0776 |
0,0748 |
0,0530 |
0,0507 |
0,0494 |
0,0468 |
0,0450 |
|
|
t 6 |
3,0918 |
0,3890 |
0,1090 |
0,0660 |
0,0452 |
0,0438 |
0,0311 |
0,0298 |
0,0294 |
0,0279 |
0,0269 |
|
|
t 7 |
0,4764 |
0,1748 |
0,0533 |
0,0326 |
0,0228 |
0,0222 |
0,0158 |
0,0152 |
0,0151 |
0,0145 |
0,0140 |
|
|
t 8 |
0,1658 |
0,0642 |
0,0202 |
0,0124 |
0,0088 |
0,0087 |
0,0061 |
0,0060 |
0,0060 |
0,0059 |
0,0056 |
|
|
t 9 |
0,0346 |
0,0135 |
0,0043 |
0,0026 |
0,0019 |
0,0019 |
0,0013 |
0,0013 |
0,0013 |
0,0013 |
0,0013 |
|
|
A |
0,9493 |
0,9407 |
0,9513 |
0,9642 |
0,9712 |
0,9762 |
0,9784 |
0,9807 |
0,9815 |
0,9817 |
0,9817 |
Таблица А.51 - Оптимальные частоты при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра двойного показательного распределения)
|
k |
Pi |
θ2 |
||||||||||
|
0,5 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
2 |
P 1 |
0,0517 |
0,0305 |
0,8094 |
0,7514 |
0,7078 |
0,6729 |
0,6452 |
0,6216 |
0,6024 |
0,5857 |
0,5710 |
|
|
P 2 |
0,9483 |
0,9695 |
0,1906 |
0,2486 |
0,2922 |
0,3271 |
0,3548 |
0,3784 |
0,3976 |
0,4143 |
0,4290 |
|
3 |
P 1 |
0,0572 |
0,0373 |
0,7098 |
0,6229 |
0,5582 |
0,5084 |
0,4695 |
0,4383 |
0,4129 |
0,3916 |
0,3738 |
|
|
P 2 |
0,8584 |
0,8306 |
0,2187 |
0,2772 |
0,3181 |
0,3472 |
0,3682 |
0,3841 |
0,3956 |
0,4044 |
0,4114 |
|
|
P 3 |
0,0844 |
0,1321 |
0,0715 |
0,0998 |
0,1237 |
0,1444 |
0,1623 |
0,1776 |
0,1913 |
0,2040 |
0,2148 |
|
4 |
P 1 |
0,0165 |
0,0103 |
0,0201 |
0,5522 |
0,4768 |
0,4195 |
0,3760 |
0,3414 |
0,3143 |
0,2917 |
0,2735 |
|
|
P 2 |
0,0878 |
0,0571 |
0,6677 |
0,2494 |
0,2807 |
0,3009 |
0,3134 |
0,3211 |
0,3255 |
0,3288 |
0,3296 |
|
|
P 3 |
0,8012 |
0,7929 |
0,2346 |
0,1497 |
0,1802 |
0,2050 |
0,2250 |
0,2420 |
0,2557 |
0,2669 |
0,2767 |
|
|
P 4 |
0,0945 |
0,1397 |
0,0776 |
0,0487 |
0,0623 |
0,0746 |
0,0856 |
0,0955 |
0,1045 |
0,1126 |
0,1202 |
|
5 |
P 1 |
0,0069 |
0,0111 |
0,0214 |
0,0121 |
0,4258 |
0,3656 |
0,3187 |
0,2839 |
0,2545 |
0,2334 |
0,2144 |
|
|
P 2 |
0,0333 |
0,0617 |
0,6023 |
0,5209 |
0,2440 |
0,2563 |
0,2649 |
0,2672 |
0,2686 |
0,2664 |
0,2658 |
|
|
P 3 |
0,0974 |
0,7073 |
0,2183 |
0,2602 |
0,1849 |
0,2956 |
0,2214 |
0,2340 |
0,2439 |
0,2513 |
0,2571 |
|
|
P 4 |
0,7629 |
0,1694 |
0,1209 |
0,1559 |
0,1103 |
0,1295 |
0,1453 |
0,1587 |
0,1704 |
0,1809 |
0,1896 |
|
|
P 5 |
0,0995 |
0,0505 |
0,0371 |
0,0509 |
0,0350 |
0,0430 |
0,0497 |
0,0562 |
0,0624 |
0,0680 |
0,0731 |
|
6 |
P 1 |
0,0071 |
0,0046 |
0,0059 |
0,0125 |
0,3912 |
0,3277 |
0,2806 |
0,2453 |
0,2159 |
0,1934 |
0,1758 |
|
|
P 2 |
0,0347 |
0,0228 |
0,0340 |
0,4728 |
0,2136 |
0,2232 |
0,2268 |
0,2272 |
0,2245 |
0,2217 |
0,2184 |
|
|
P 3 |
0,1027 |
0,0700 |
0,5718 |
0,2305 |
0,1750 |
0,1913 |
0,2041 |
0,2127 |
0,2182 |
0,2235 |
0,2269 |
|
|
P 4 |
0,6968 |
0,6751 |
0,2254 |
0,1634 |
0,1268 |
0,1446 |
0,1596 |
0,1714 |
0,1830 |
0,1908 |
0,1981 |
|
|
P 5 |
0,1244 |
0,1756 |
0,1246 |
0,0927 |
0,0717 |
0,0856 |
0,0977 |
0,1080 |
0,1185 |
0,1269 |
0,1339 |
|
|
P 6 |
0,0343 |
0,0519 |
0,0383 |
0,0281 |
0,0217 |
0,0266 |
0,0312 |
0,0354 |
0,0399 |
0,0437 |
0,0469 |
|
7 |
P 1 |
0,0037 |
0,0047 |
0,0060 |
0,0131 |
0,0076 |
0,3019 |
0,2528 |
0,2170 |
0,1891 |
0,1670 |
0,1490 |
|
|
P 2 |
0,0170 |
0,0236 |
0,0356 |
0,4396 |
0,3688 |
0,1963 |
0,1970 |
0,1958 |
0,1919 |
0,1882 |
0,1828 |
|
|
P 3 |
0,0458 |
0,0728 |
0,5268 |
0,2058 |
0,2188 |
0,1748 |
0,1833 |
0,1900 |
0,1936 |
0,1959 |
0,1971 |
|
|
P 4 |
0,1051 |
0,6203 |
0,2034 |
0,1579 |
0,1793 |
0,1451 |
0,1579 |
0,1674 |
0,1758 |
0,1820 |
0,1869 |
|
|
P 5 |
0,6632 |
0,1694 |
0,1350 |
0,1085 |
0,1297 |
0,1051 |
0,1187 |
0,1288 |
0,1385 |
0,1467 |
0,1547 |
|
|
P 6 |
0,1295 |
0,0850 |
0,0722 |
0,0582 |
0,0736 |
0,0592 |
0,0693 |
0,0770 |
0,0843 |
0,0909 |
0,0975 |
|
|
P 7 |
0,0357 |
0,0242 |
0,0210 |
0,0169 |
0,0222 |
0,0175 |
0,0210 |
0,0239 |
0,0268 |
0,0293 |
0,0320 |
|
8 |
P 1 |
0,0020 |
0,0024 |
0,0025 |
0,0034 |
0,0079 |
0,2816 |
0,2334 |
0,1966 |
0,1698 |
0,1465 |
0,1302 |
|
|
P 2 |
0,0092 |
0,0113 |
0,0130 |
0,0209 |
0,3412 |
0,1735 |
0,1744 |
0,1707 |
0,1674 |
0,1619 |
0,1569 |
|
|
P 3 |
0,0239 |
0,0315 |
0,0405 |
0,4176 |
0,1960 |
0,1594 |
0,1659 |
0,1683 |
0,1722 |
0,1718 |
0,1723 |
|
|
P 4 |
0,0512 |
0,0754 |
0,5053 |
0,2083 |
0,1663 |
0,1394 |
0,1494 |
0,1573 |
0,1636 |
0,1681 |
0,1706 |
|
|
P 5 |
0,1041 |
0,5953 |
0,2066 |
0,1602 |
0,1318 |
0,1125 |
0,1232 |
0,1339 |
0,1412 |
0,1488 |
0,1538 |
|
|
P 6 |
0,6411 |
0,1733 |
0,1371 |
0,1111 |
0,1921 |
0,0787 |
0,0891 |
0,0998 |
0,1059 |
0,1143 |
0,1204 |
|
|
P 7 |
0,1320 |
0,0862 |
0,0735 |
0,0607 |
0,0502 |
0,0427 |
0,0500 |
0,0565 |
0,0614 |
0,0677 |
0,0731 |
|
|
P 8 |
0,0365 |
0,0246 |
0,0215 |
0,0178 |
0,0145 |
0,0122 |
0,0146 |
0,0109 |
0,0186 |
0,0209 |
0,0227 |
|
9 |
P 1 |
0,0021 |
0,0023 |
0,0025 |
0,0036 |
0,0082 |
0,0049 |
0,2166 |
0,1801 |
0,1527 |
0,1314 |
0,1167 |
|
|
P 2 |
0,0099 |
0,0113 |
0,0131 |
0,0218 |
0,3227 |
0,2651 |
0,1541 |
0,1521 |
0,1466 |
0,1412 |
0,1374 |
|
|
P 3 |
0,0256 |
0,0316 |
0,0419 |
0,3886 |
0,1763 |
0,1775 |
0,1501 |
0,1517 |
0,1532 |
0,1530 |
0,1537 |
|
|
P 4 |
0,0539 |
0,0772 |
0,4734 |
0,1878 |
0,1530 |
0,1629 |
0,1393 |
0,1458 |
0,1497 |
0,1523 |
0,1555 |
|
|
P 5 |
0,1076 |
0,5587 |
0,1877 |
0,1512 |
0,1285 |
0,1421 |
0,1228 |
0,1308 |
0,1373 |
0,1426 |
0,1465 |
|
|
P 6 |
0,5917 |
0,1597 |
0,1344 |
0,1162 |
0,0995 |
0,1137 |
0,0999 |
0,1075 |
0,1150 |
0,1223 |
0,1257 |
|
|
P 7 |
0,1308 |
0,0970 |
0,0883 |
0,0781 |
0,0672 |
0,0789 |
0,0691 |
0,0774 |
0,0842 |
0,0903 |
0,0945 |
|
|
P 8 |
0,0616 |
0,0487 |
0,0459 |
0,0411 |
0,0348 |
0,0428 |
0,0374 |
0,0423 |
0,0474 |
0,0515 |
0,0538 |
|
|
P 9 |
0,0168 |
0,0135 |
0,0128 |
0,0116 |
0,0098 |
0,0121 |
0,0107 |
0,0123 |
0,0139 |
0,0154 |
0,0162 |
|
10 |
P 1 |
0,0013 |
0,0013 |
0,0026 |
0,0037 |
0,0083 |
0,0052 |
0,2057 |
0,1694 |
0,1401 |
0,1206 |
0,1045 |
|
|
P 2 |
0,0059 |
0,0060 |
0,0133 |
0,0222 |
0,3037 |
0,2430 |
0,1403 |
0,1372 |
0,1299 |
0,1264 |
0,1207 |
|
|
P 3 |
0,0148 |
0,0161 |
0,0435 |
0,3678 |
0,1578 |
0,1570 |
0,1350 |
0,1372 |
0,1359 |
0,1361 |
0,1351 |
|
|
P 4 |
0,0305 |
0,0360 |
0,4446 |
0,1704 |
0,1406 |
0,1478 |
0,1282 |
0,1334 |
0,1360 |
0,1389 |
0,1397 |
|
|
P 5 |
0,0563 |
0,0773 |
0,1702 |
0,1411 |
0,1228 |
0,1348 |
0,1185 |
0,1238 |
0,1319 |
0,1342 |
0,1377 |
|
|
P 6 |
0,1043 |
0,5411 |
0,1300 |
0,1152 |
0,1015 |
0,1155 |
0,1019 |
0,1104 |
0,1166 |
0,1215 |
0,1263 |
|
|
P 7 |
0,5749 |
0,1619 |
0,0947 |
0,0865 |
0,0780 |
0,0914 |
0,0798 |
0,0875 |
0,0955 |
0,1001 |
0,1052 |
|
|
P 8 |
0,1324 |
0,0982 |
0,0615 |
0,0567 |
0,0526 |
0,0628 |
0,0546 |
0,0602 |
0,0673 |
0,0715 |
0,0761 |
|
|
P 9 |
0,0624 |
0,0488 |
0,0310 |
0,0285 |
0,0273 |
0,0332 |
0,0282 |
0,0320 |
0,0364 |
0,0393 |
0,0423 |
|
|
P 10 |
0,0172 |
0,0133 |
0,0086 |
0,0079 |
0,0074 |
0,0093 |
0,0078 |
0,0089 |
0,0104 |
0,0114 |
0,0124 |
Таблица А.52 - Оптимальные граничные точки интервалов группирования при проверке простых и сложных гипотез по критериям типа χ2 (при оценивании двух параметров двойного показательного распределения) и соответствующие значения относительной асимптотической информации А
|
k |
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t 6 |
t 7 |
t 8 |
t 9 |
t 10 |
t 11 |
t 12 |
t 13 |
t 14 |
A |
|
3 |
2,6067 |
0,2731 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,4079 |
|
4 |
3,4137 |
1,3979 |
0,2109 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5572 |
|
5 |
3,8606 |
1,9590 |
0,5123 |
0,1044 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,6836 |
|
6 |
4,4096 |
2,5726 |
1,2269 |
0,3649 |
0,0772 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,7571 |
|
7 |
4,7959 |
2,9922 |
1,7192 |
0,6758 |
0,2318 |
0,0501 |
- |
- |
- |
- |
- |
- |
- |
- |
0,8109 |
|
8 |
5,2049 |
3,4285 |
2,2041 |
1,1904 |
0,4837 |
0,1740 |
0,0377 |
- |
- |
- |
- |
- |
- |
- |
0,8480 |
|
9 |
5,5273 |
3,7667 |
2,5713 |
1,6027 |
0,7829 |
0,3431 |
1,1269 |
0,0275 |
- |
- |
- |
- |
- |
- |
0,8756 |
|
10 |
5,8478 |
4,1024 |
2,9269 |
1,9932 |
1,1805 |
0,5770 |
0,2638 |
0,0988 |
0,0213 |
- |
- |
- |
- |
- |
0,8963 |
|
11 |
6,1270 |
4,3930 |
3,2319 |
2,3192 |
1,5344 |
0,8560 |
0,4359 |
0,2046 |
0,0771 |
0,0165 |
- |
- |
- |
- |
0,9123 |
|
12 |
6,3853 |
4,6589 |
3,5103 |
2,6163 |
1,8570 |
1,1789 |
0,6517 |
0,3434 |
0,1638 |
0,0618 |
0,0123 |
- |
- |
- |
0,9248 |
|
13 |
6,6208 |
4,9016 |
3,7623 |
2,8810 |
2,1401 |
1,4807 |
0,9030 |
0,5106 |
0,2754 |
0,1326 |
0,0500 |
0,0106 |
- |
- |
0,9349 |
|
14 |
6,8444 |
5,1314 |
3,9997 |
3,1286 |
2,4019 |
1,7608 |
1,1798 |
0,7116 |
0,3126 |
0,2261 |
0,1094 |
0,0412 |
0,0087 |
- |
0,9431 |
|
15 |
7,0506 |
5,3425 |
4,2169 |
3,3538 |
2,6381 |
2,0116 |
1,4426 |
0,9387 |
0,5734 |
0,3394 |
0,1881 |
0,0913 |
0,0344 |
0,0072 |
0,9498 |
Таблица А.53 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании основного параметра θ0 гамма-распределения в зависимости от его значений) и соответствующие значения относительной асимптотической информации А
|
k |
ti |
θ 0 |
||||||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
2 |
t 1 |
0,0001 |
0,0015 |
0,0513 |
0,1847 |
0,3697 |
1,2770 |
2,2507 |
3,2389 |
4,2389 |
5,2276 |
6,2246 |
7,2223 |
8,2209 |
|
|
А |
0,5582 |
0,6349 |
0,6241 |
0,6213 |
0,6217 |
0,6266 |
0,6295 |
0,6312 |
0,6312 |
0,6330 |
0,6335 |
0,6342 |
0,6342 |
|
3 |
t 1 |
0,0001 |
0,0001 |
0,0072 |
0,0486 |
0,1320 |
0,7104 |
1,4483 |
2,2477 |
3,0797 |
3,9331 |
4,7998 |
5,6776 |
6,5651 |
|
|
t 2 |
0,0107 |
0,0119 |
0,1849 |
0,4548 |
0,7585 |
2,0041 |
3,2128 |
4,3894 |
5,5430 |
6,6830 |
7,8083 |
8,9249 |
10,0345 |
|
|
А |
0,5899 |
0,8030 |
0,8016 |
0,7994 |
0,7993 |
0,8024 |
0,8045 |
0,8058 |
0,8065 |
0,8071 |
0,8075 |
0,8077 |
0,8080 |
|
4 |
t 1 |
0,0001 |
0,0001 |
0,0017 |
0,0183 |
0,0628 |
0,4750 |
1,0777 |
1,7666 |
2,5032 |
3,2712 |
4,0605 |
4,8667 |
5,6859 |
|
|
t 2 |
0,0024 |
0,0046 |
0,0407 |
0,1593 |
0,3309 |
1,2132 |
2,1777 |
3,1630 |
4,1555 |
5,1501 |
6,1471 |
7,1423 |
8,1399 |
|
|
t 3 |
0,0598 |
0,1029 |
0,3422 |
0,7193 |
1,1017 |
2,5616 |
3,9121 |
5,2047 |
6,4588 |
7,6841 |
8,8927 |
10,0770 |
11,2527 |
|
|
А |
0,5964 |
0,8594 |
0,8771 |
0,8754 |
0,8753 |
0,8772 |
0,8787 |
0,8796 |
0,8801 |
0,8805 |
0,8808 |
0,8810 |
0,8812 |
|
5 |
t 1 |
0,0001 |
0,0001 |
0,0005 |
0,0085 |
0,0354 |
0,3472 |
0,8613 |
1,4748 |
2,1424 |
2,8509 |
3,5885 |
4,3438 |
5,1164 |
|
|
t 2 |
0,0010 |
0,0021 |
0,0128 |
0,0721 |
0,1805 |
0,8501 |
1,6675 |
2,5337 |
3,4201 |
4,3267 |
5,2437 |
6,1642 |
7,0915 |
|
|
t 3 |
0,0117 |
0,0325 |
0,1009 |
0,2965 |
0,5452 |
1,6339 |
2,7524 |
3,8565 |
4,9443 |
6,0309 |
7,1122 |
8,1814 |
9,2491 |
|
|
t 4 |
0,1236 |
0,2779 |
0,5111 |
0,9639 |
1,4159 |
3,0120 |
4,4759 |
5,8487 |
7,1625 |
8,4527 |
9,7195 |
10,9557 |
12,1801 |
|
|
A |
0,5987 |
0,8786 |
0,9162 |
0,9150 |
0,9148 |
0,9161 |
0,9172 |
0,9179 |
0,9183 |
0,9186 |
0,9188 |
0,9189 |
0,9191 |
|
6 |
t 1 |
0,0001 |
0,0001 |
0,0002 |
0,0044 |
0,0215 |
0,2687 |
0,7181 |
1,2744 |
1,8922 |
2,5580 |
3,2519 |
3,9678 |
4,7046 |
|
|
t 2 |
0,0007 |
0,0013 |
0,0053 |
0,0374 |
0,1083 |
0,6423 |
1,3543 |
2,1362 |
2,9496 |
3,7960 |
4,6533 |
5,5169 |
6,3949 |
|
|
t 3 |
0,0067 |
0,0133 |
0,0412 |
0,1497 |
0,3154 |
1,1836 |
2,1466 |
3,1328 |
4,1173 |
5,1224 |
6,1180 |
7,1093 |
8,1070 |
|
|
t 4 |
0,0496 |
0,0894 |
0,1930 |
0,4426 |
0,7422 |
1,9977 |
3,2241 |
4,4200 |
5,5757 |
6,7415 |
7,8782 |
8,9940 |
10,1176 |
|
|
t 5 |
0,3139 |
0,4711 |
0,7737 |
1,1900 |
1,6659 |
3,3991 |
4,9418 |
6,3832 |
7,7412 |
9,1011 |
10,4031 |
11,6661 |
12,9383 |
|
|
A |
0,5998 |
0,8879 |
0,9389 |
0,9383 |
0,9381 |
0,9390 |
0,9399 |
0,9403 |
0,9407 |
0,9409 |
0,9410 |
0,9412 |
0,9412 |
|
7 |
t 1 |
0,0001 |
0,0001 |
0,0001 |
0,0026 |
0,0146 |
0,2171 |
0,6186 |
1,1309 |
1,7093 |
2,3332 |
2,9988 |
3,6820 |
4,3897 |
|
|
t 2 |
0,0005 |
0,0008 |
0,0031 |
0,0218 |
0,0731 |
0,5102 |
1,1471 |
1,8632 |
2,6240 |
3,4080 |
4,2263 |
5,0457 |
5,8840 |
|
|
t 3 |
0,0030 |
0,0055 |
0,0243 |
0,0864 |
0,2092 |
0,9178 |
1,7754 |
2,6727 |
3,5869 |
4,5057 |
5,4518 |
6,3835 |
7,3311 |
|
|
t 4 |
0,0161 |
0,0281 |
0,1128 |
0,2461 |
0,4752 |
1,4858 |
2,5661 |
3,6407 |
4,7026 |
5,7498 |
6,8211 |
7,8579 |
8,9109 |
|
|
t 5 |
0,0785 |
0,1281 |
0,4070 |
0,6139 |
0,9682 |
2,3185 |
3,6392 |
4,9055 |
6,1241 |
7,3089 |
8,5154 |
9,6612 |
10,8234 |
|
|
t 6 |
0,3641 |
0,5483 |
1,1660 |
1,4213 |
1,9761 |
3,7328 |
5,3499 |
6,8529 |
8,2562 |
9,6122 |
10,9755 |
12,2600 |
13,5624 |
|
|
A |
0,6004 |
0,8935 |
0,9521 |
0,9531 |
0,9529 |
0,9535 |
0,9543 |
0,9547 |
0,9549 |
0,9551 |
0,9552 |
0,9553 |
0,9554 |
|
8 |
t 1 |
0,0001 |
0,0001 |
0,0001 |
0,0016 |
0,0098 |
0,1784 |
0,5404 |
1,0152 |
1,5649 |
2,1542 |
2,7984 |
3,4508 |
4,1331 |
|
|
t 2 |
0,0004 |
0,0005 |
0,0011 |
0,0131 |
0,0489 |
0,4155 |
0,9904 |
1,6520 |
2,3718 |
3,1110 |
3,9004 |
4,6821 |
5,4852 |
|
|
t 3 |
0,0019 |
0,0030 |
0,0073 |
0,0515 |
0,1381 |
0,7355 |
1,5094 |
2,3329 |
3,1953 |
4,0582 |
4,9692 |
5,8519 |
6,7541 |
|
|
t 4 |
0,0088 |
0,0137 |
0,0305 |
0,1450 |
0,3061 |
1,1623 |
2,1332 |
3,1107 |
4,1077 |
5,0847 |
6,1093 |
7,0845 |
8,0765 |
|
|
t 5 |
0,0364 |
0,0540 |
0,1008 |
0,3414 |
0,5997 |
1,7435 |
2,9199 |
4,0545 |
5,1847 |
6,2784 |
7,4181 |
8,4880 |
9,5668 |
|
|
t 6 |
0,1372 |
0,1911 |
0,2947 |
0,7368 |
1,1125 |
2,5864 |
3,9929 |
5,3042 |
6,5736 |
7,7931 |
9,0609 |
10,2371 |
11,4088 |
|
|
t 7 |
0,5132 |
0,6608 |
0,8568 |
1,6048 |
2,1277 |
4,0015 |
5,7046 |
7,2378 |
8,6726 |
10,0464 |
11,4837 |
12,7955 |
14,0743 |
|
|
A |
0,6008 |
0,8968 |
0,9632 |
0,9631 |
0,9630 |
0,9634 |
0,9641 |
0,9644 |
0,9646 |
0,9647 |
0,9648 |
0,9649 |
0,9650 |
|
9 |
t 1 |
0,0001 |
0,0001 |
0,0001 |
0,0013 |
0,0070 |
0,1530 |
0,4820 |
0,9280 |
1,4472 |
2,0142 |
2,6267 |
3,2788 |
3,9300 |
|
|
t 2 |
0,0004 |
0,0006 |
0,0012 |
0,0109 |
0,0348 |
0,3528 |
0,8748 |
1,4972 |
2,1744 |
2,8840 |
3,6306 |
4,4127 |
5,1757 |
|
|
t 3 |
0,0020 |
0,0035 |
0,0085 |
0,0426 |
0,0979 |
0,6176 |
1,3174 |
2,0917 |
2,8984 |
3,7253 |
4,5811 |
5,4663 |
6,3141 |
|
|
t 4 |
0,0088 |
0,0162 |
0,0359 |
0,1181 |
0,2136 |
0,9611 |
1,8339 |
2,7493 |
3,6755 |
4,6078 |
5,5630 |
6,5453 |
7,4689 |
|
|
t 5 |
0,0338 |
0,0579 |
0,1080 |
0,2673 |
0,4088 |
1,4083 |
2,4560 |
3,5096 |
4,5561 |
5,5877 |
6,6434 |
7,7191 |
8,7179 |
|
|
t 6 |
0,1045 |
0,1629 |
0,2658 |
0,5513 |
0,7273 |
2,0082 |
3,2445 |
4,4375 |
5,6109 |
6,7483 |
7,9071 |
9,0767 |
10,1554 |
|
|
t 7 |
0,2544 |
0,3677 |
0,6014 |
1,1038 |
1,2617 |
2,8682 |
4,3192 |
5,6654 |
6,9793 |
8,2363 |
9,5076 |
10,7895 |
11,9544 |
|
|
t 8 |
0,7853 |
0,9597 |
1,3541 |
1,9491 |
2,3730 |
4,2945 |
6,0374 |
7,5654 |
9,0699 |
10,4673 |
11,8848 |
13,3029 |
14,5811 |
|
|
A |
0,6010 |
0,8983 |
0,9694 |
0,9696 |
0,9701 |
0,9704 |
0,9710 |
0,9713 |
0,9714 |
0,9715 |
0,9716 |
0,9717 |
0,9717 |
|
10 |
t 1 |
0,0001 |
0,0001 |
0,0001 |
0,0008 |
0,0057 |
0,1286 |
0,4338 |
0,8578 |
1,3486 |
1,9032 |
2,4925 |
3,1060 |
3,7579 |
|
|
t 2 |
0,0003 |
0,0003 |
0,0006 |
0,0066 |
0,0283 |
0,2949 |
0,7825 |
1,3747 |
2,0130 |
2,7092 |
3,4238 |
4,1501 |
4,9167 |
|
|
t 3 |
0,0016 |
0,0012 |
0,0026 |
0,0256 |
0,0795 |
0,5129 |
1,1686 |
1,9036 |
2,6636 |
3,4726 |
4,2864 |
5,1051 |
5,9607 |
|
|
t 4 |
0,0064 |
0,0042 |
0,0090 |
0,0708 |
0,1728 |
0,7908 |
1,6095 |
2,4773 |
3,3469 |
4,2579 |
5,1601 |
6,0628 |
6,9967 |
|
|
t 5 |
0,0234 |
0,0130 |
0,0261 |
0,1615 |
0,3261 |
1,1420 |
2,1240 |
3,1212 |
4,0977 |
5,1035 |
6,0920 |
7,0735 |
8,0841 |
|
|
t 6 |
0,0744 |
0,0370 |
0,0676 |
0,3289 |
0,5665 |
1,5937 |
2,7466 |
3,8739 |
4,9577 |
6,0581 |
7,1346 |
8,1975 |
9,2821 |
|
|
t 7 |
0,2103 |
0,0994 |
0,1652 |
0,6304 |
0,9409 |
2,1950 |
3,5364 |
4,8009 |
5,9965 |
7,1919 |
8,3648 |
9,5131 |
10,6742 |
|
|
t 8 |
0,4568 |
0,2598 |
0,3972 |
1,1740 |
1,5499 |
3,0541 |
4,6113 |
6,0295 |
7,3547 |
8,6527 |
9,9446 |
11,1855 |
12,4307 |
|
|
t 9 |
1,0251 |
0,7082 |
1,0120 |
2,5526 |
2,7021 |
4,4768 |
6,3189 |
7,9303 |
9,4257 |
10,8507 |
12,3101 |
13,6776 |
15,0095 |
|
|
A |
0,6011 |
0,9003 |
0,9734 |
0,9747 |
0,9754 |
0,9755 |
0,9761 |
0,9763 |
0,9765 |
0,9766 |
0,9766 |
0,9767 |
0,9767 |
Таблица A.54 - Оптимальные вероятности (частоты) интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании основного параметра θ0 гамма-распределения в зависимости от его значений) и соответствующие значения относительной асимптотической информации А
|
k |
Pi |
θ 0 |
||||||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
2 |
P 1 |
0,4185 |
0,2171 |
0,2513 |
0,2837 |
0,3091 |
0,3650 |
0,3908 |
0,4061 |
0,4177 |
0,4239 |
0,4297 |
0,4344 |
0,4383 |
|
|
P 2 |
0,5815 |
0,7829 |
0,7487 |
0,7163 |
0,6909 |
0,6350 |
0,6092 |
0,5939 |
0,5823 |
0,5761 |
0,5703 |
0,5656 |
0,5617 |
|
3 |
P 1 |
0,4185 |
0,1103 |
0,0955 |
0,1103 |
0,1237 |
0,1594 |
0,1783 |
0,1901 |
0,1983 |
0,2045 |
0,2092 |
0,2130 |
0,2162 |
|
|
P 2 |
0,2487 |
0,2533 |
0,3614 |
0,3901 |
0,4080 |
0,4357 |
0,4445 |
0,4486 |
0,4508 |
0,4525 |
0,4535 |
0,4543 |
0,4548 |
|
|
P 3 |
0,3329 |
0,6365 |
0,5431 |
0,4996 |
0,4684 |
0,4049 |
0,3772 |
0,3613 |
0,3509 |
0,3430 |
0,3373 |
0,3328 |
0,3289 |
|
4 |
P 1 |
0,4185 |
0,1103 |
0,0465 |
0,0537 |
0,0609 |
0,0827 |
0,0951 |
0,1034 |
0,1092 |
0,1137 |
0,1171 |
0,1198 |
0,1221 |
|
|
P 2 |
0,1564 |
0,1767 |
0,1781 |
0,2028 |
0,2209 |
0,2594 |
0,2762 |
0,2858 |
0,2923 |
0,2967 |
0,3002 |
0,3027 |
0,3049 |
|
|
P 3 |
0,2140 |
0,3253 |
0,3673 |
0,3821 |
0,3860 |
0,3830 |
0,3774 |
0,3733 |
0,3702 |
0,3677 |
0,3660 |
0,3642 |
0,3627 |
|
|
P 4 |
0,2111 |
0,3876 |
0,4081 |
0,3614 |
0,3323 |
0,2749 |
0,2513 |
0,2375 |
0,2283 |
0,2219 |
0,2167 |
0,2134 |
0,2103 |
|
5 |
P 1 |
0,4185 |
0,1103 |
0,0252 |
0,0303 |
0,0348 |
0,0480 |
0,0566 |
0,0625 |
0,0664 |
0,0696 |
0,0723 |
0,0743 |
0,0760 |
|
|
P 2 |
0,1083 |
0,1258 |
0,1019 |
0,1165 |
0,1304 |
0,1613 |
0,1776 |
0,1871 |
0,1931 |
0,1981 |
0,2019 |
0,2046 |
0,2070 |
|
|
P 3 |
0,1462 |
0,2293 |
0,2196 |
0,2397 |
0,2551 |
0,2766 |
0,2849 |
0,2884 |
0,2901 |
0,2915 |
0,2926 |
0,2931 |
0,2938 |
|
|
P 4 |
0,1705 |
0,2943 |
0,3413 |
0,3424 |
0,3370 |
0,3167 |
0,3046 |
0,2968 |
0,2916 |
0,2875 |
0,2843 |
0,2819 |
0,2797 |
|
|
P 5 |
0,1565 |
0,2403 |
0,3120 |
0,2711 |
0,2427 |
0,1974 |
0,1763 |
0,1652 |
0,1587 |
0,1532 |
0,1488 |
0,1461 |
0,1436 |
|
6 |
P 1 |
0,4185 |
0,1103 |
0,0160 |
0,0186 |
0,0213 |
0,0302 |
0,0364 |
0,0406 |
0,0435 |
0,0460 |
0,0478 |
0,0492 |
0,0505 |
|
|
P 2 |
0,0899 |
0,0991 |
0,0660 |
0,0725 |
0,0814 |
0,1058 |
0,1192 |
0,1277 |
0,1329 |
0,1378 |
0,1412 |
0,1434 |
0,1456 |
|
|
P 3 |
0,1285 |
0,1642 |
0,1439 |
0,1548 |
0,1679 |
0,1954 |
0,2074 |
0,2142 |
0,2177 |
0,2217 |
0,2236 |
0,2250 |
0,2263 |
|
|
P 4 |
0,1381 |
0,2191 |
0,2397 |
0,2468 |
0,2534 |
0,2619 |
0,2622 |
0,2615 |
0,2601 |
0,2596 |
0,2589 |
0,2578 |
0,2579 |
|
|
P 5 |
0,1365 |
0,2453 |
0,3209 |
0,2982 |
0,2870 |
0,2597 |
0,2453 |
0,2358 |
0,2304 |
0,2252 |
0,2218 |
0,2195 |
0,2171 |
|
|
P 6 |
0,0885 |
0,1619 |
0,2125 |
0,2092 |
0,1890 |
0,1469 |
0,1296 |
0,1201 |
0,1154 |
0,1097 |
0,1067 |
0,1051 |
0,1026 |
|
7 |
P 1 |
0,4185 |
0,1103 |
0,0113 |
0,0125 |
0,0145 |
0,0204 |
0,0250 |
0,0281 |
0,0302 |
0,0318 |
0,0334 |
0,0344 |
0,0354 |
|
|
P 2 |
0,0731 |
0,0752 |
0,0515 |
0,0486 |
0,0560 |
0,0729 |
0,0843 |
0,0910 |
0,0958 |
0,0987 |
0,1021 |
0,1038 |
0,1057 |
|
|
P 3 |
0,0963 |
0,1146 |
0,1117 |
0,1060 |
0,1183 |
0,1407 |
0,1536 |
0,1608 |
0,1651 |
0,1676 |
0,1708 |
0,1721 |
0,1740 |
|
|
P 4 |
0,1067 |
0,1491 |
0,1907 |
0,1759 |
0,1895 |
0,2034 |
0,2102 |
0,2135 |
0,2148 |
0,2153 |
0,2169 |
0,2167 |
0,2176 |
|
|
P 5 |
0,1147 |
0,1945 |
0,2679 |
0,2466 |
0,2420 |
0,2360 |
0,2311 |
0,2281 |
0,2253 |
0,2236 |
0,2222 |
0,2207 |
0,2194 |
|
|
P 6 |
0,1122 |
0,2156 |
0,2402 |
0,2492 |
0,2412 |
0,2134 |
0,1978 |
0,1888 |
01829 |
0,1798 |
0,1749 |
0,1736 |
0,1714 |
|
|
P 7 |
0,0786 |
0,1407 |
0,1267 |
0,1612 |
0,1386 |
0,1132 |
0,0981 |
0,0898 |
0,0859 |
0,0833 |
0,0796 |
0,0787 |
0,0767 |
|
8 |
P 1 |
0,4185 |
0,1103 |
0,0113 |
0,0087 |
0,0098 |
0,0141 |
0,0176 |
0,0199 |
0,0218 |
0,0228 |
0,0243 |
0,0249 |
0,0256 |
|
|
P 2 |
0,0622 |
0,0546 |
0,0261 |
0,0332 |
0,0380 |
0,0516 |
0,0609 |
0,0662 |
0,0706 |
0,0727 |
0,0762 |
0,0775 |
0,0788 |
|
|
P 3 |
0,0810 |
0,0931 |
0,0588 |
0,0732 |
0,0813 |
0,1025 |
0,1150 |
0,1212 |
0,1262 |
0,1285 |
0,1328 |
0,1336 |
0,1351 |
|
|
P 4 |
0,0926 |
0,1184 |
0,0989 |
0,1254 |
0,1347 |
0,1555 |
0,1658 |
0,1702 |
0,1736 |
0,1749 |
0,1779 |
0,1780 |
0,1787 |
|
|
P 5 |
0,0979 |
0,1498 |
0,1515 |
0,1815 |
0,1873 |
0,1964 |
01993 |
0,1996 |
0,1991 |
0,1990 |
0,1993 |
0,1990 |
0,1982 |
|
|
P 6 |
0,0992 |
0,1768 |
0,2108 |
0,2241 |
0,2202 |
0,2098 |
0,2022 |
0,1980 |
0,1931 |
0,1911 |
0,1882 |
0,1875 |
0,1859 |
|
|
P 7 |
0,0915 |
0,1811 |
0,2521 |
0,2226 |
0,2096 |
0,1786 |
0,1626 |
0,1547 |
0,1485 |
0,1456 |
0,1405 |
0,1396 |
0,1379 |
|
|
P 8 |
0,0571 |
0,1159 |
0,1905 |
0,1314 |
0,1191 |
0,0915 |
0,0765 |
0,0702 |
0,0671 |
0,0654 |
0,0608 |
0,0601 |
0,0598 |
|
9 |
P 1 |
0,4185 |
0,1103 |
0,0113 |
0,0074 |
0,0070 |
0,0106 |
0,0131 |
0,0149 |
0,0162 |
0,0171 |
0,0180 |
0,0191 |
0,0194 |
|
|
P 2 |
0,0622 |
0,0623 |
0,0278 |
0,0291 |
0,0272 |
0,0388 |
0,0457 |
0,0504 |
0,0536 |
0,0556 |
0,0578 |
0,0604 |
0,0608 |
|
|
P 3 |
0,0839 |
0,0955 |
0,0647 |
0,0637 |
0,0591 |
0,0784 |
0,0881 |
0,0945 |
0,0982 |
0,1009 |
0,1037 |
0,1068 |
0,1067 |
|
|
P 4 |
0,0898 |
0,1242 |
0,1075 |
0,1083 |
0,0991 |
0,1222 |
0,1316 |
0,1370 |
0,1401 |
0,1420 |
0,1444 |
0,1475 |
0,1469 |
|
|
P 5 |
0,0926 |
0,1427 |
0,1466 |
0,1533 |
0,1432 |
0,1611 |
0,1664 |
0,1686 |
0,1705 |
0,1705 |
0,1720 |
0,1733 |
0,1729 |
|
|
P 6 |
0,0840 |
0,1440 |
0,1762 |
0,1952 |
0,1812 |
0,1852 |
0,1845 |
0,1816 |
0,1810 |
0,1799 |
0,1792 |
0,1778 |
0,1778 |
|
|
P 7 |
0,0659 |
0,1228 |
0,1932 |
0,2122 |
0,2000 |
0,1841 |
0,1757 |
0,1693 |
0,1656 |
0,1635 |
0,1605 |
0,1577 |
0,1576 |
|
|
P 8 |
0,0687 |
0,1260 |
0,1729 |
0,1409 |
0,1900 |
0,1475 |
0,1346 |
0,1270 |
0,1222 |
0,1192 |
0,1155 |
0,1112 |
0,1116 |
|
|
P 9 |
0,0345 |
0,0722 |
0,0998 |
0,0899 |
0,0932 |
0,0722 |
0,0603 |
0,0567 |
0,0527 |
0,0513 |
0,0488 |
0,0461 |
0,0464 |
|
10 |
P 1 |
0,4185 |
0,1103 |
0,0113 |
0,0052 |
0,0057 |
0,0076 |
0,0099 |
0,0115 |
0,0123 |
0,0133 |
0,0140 |
0,0144 |
0,0150 |
|
|
P 2 |
0,0486 |
0,0349 |
0,0164 |
0,0199 |
0,0222 |
0,0282 |
0,0351 |
0,0394 |
0,0415 |
0,0442 |
0,0456 |
0,0462 |
0,0478 |
|
|
P 3 |
0,0850 |
0,0601 |
0,0299 |
0,0438 |
0,0485 |
0,0583 |
0,0688 |
0,0750 |
0,0779 |
0,0813 |
0,0830 |
0,0840 |
0,0859 |
|
|
P 4 |
0,0818 |
0,0753 |
0,0492 |
0,0760 |
0,0823 |
0,0938 |
0,1053 |
0,1117 |
0,1143 |
0,1176 |
0,1190 |
0,1201 |
0,1217 |
|
|
P 5 |
0,0866 |
0,0909 |
0,0740 |
0,1140 |
0,1196 |
0,1284 |
0,1377 |
0,1423 |
0,1442 |
0,1458 |
0,1469 |
0,1475 |
0,1487 |
|
|
P 6 |
0,0847 |
0,1088 |
0,1062 |
0,1534 |
0,1542 |
0,1567 |
0,1609 |
0,1616 |
0,1618 |
0,1614 |
0,1617 |
0,1620 |
0,1617 |
|
|
P 7 |
0,0778 |
0,1272 |
0,1477 |
0,1854 |
0,1772 |
0,1712 |
0,1681 |
0,1644 |
0,1624 |
0,1595 |
0,1590 |
0,1584 |
0,1569 |
|
|
P 8 |
0,0528 |
0,1420 |
0,1927 |
0,1892 |
0,1780 |
0,1646 |
0,1527 |
0,1455 |
0,1425 |
0,1384 |
0,1372 |
0,1357 |
0,1334 |
|
|
P 9 |
0,0409 |
0,1434 |
0,2179 |
0,1663 |
0,1452 |
0,1289 |
0,1123 |
0,1042 |
0,1008 |
0,0975 |
0,0952 |
0,0939 |
0,0915 |
|
|
P 10 |
0,0233 |
0,1071 |
0,1548 |
0,0467 |
0,0671 |
0,0623 |
0,0492 |
0,0444 |
0,0422 |
0,0410 |
0,0385 |
0,0377 |
0,0373 |
Таблица А.55 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра гамма-распределения и известных значениях основного параметра θ0) и соответствующие значения относительной асимптотической информации А
|
k |
ti |
θ 0 |
||||||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
2 |
t 1 |
0,7065 |
0,8525 |
1,0982 |
1,3455 |
1,5936 |
2,5897 |
3,5881 |
4,5877 |
5,5870 |
6,5859 |
7,5862 |
8,5859 |
9,5857 |
|
|
А |
0,6598 |
0,6563 |
0,6522 |
0,6495 |
0,6476 |
0,6435 |
0,6416 |
0,6405 |
0,6398 |
0,6393 |
0,6390 |
0,6387 |
0,6385 |
|
3 |
t 1 |
0,3798 |
0,4780 |
0,6499 |
0,8305 |
1,0178 |
1,8046 |
2,6312 |
2,6312 |
3,4804 |
4,3449 |
5,2218 |
6,1064 |
6,9992 |
|
|
t 2 |
1,4817 |
1,6753 |
1,9909 |
2,3027 |
2,6117 |
3,8120 |
4,9820 |
4,9820 |
6,1305 |
7,2633 |
8,3868 |
9,4992 |
10,6068 |
|
|
А |
0,8308 |
0,8279 |
0,8244 |
0,8220 |
0,8203 |
0,8164 |
0,8146 |
0,8146 |
0,8136 |
0,8129 |
0,8125 |
0,8121 |
0,8119 |
|
4 |
t 1 |
0,2500 |
0,3231 |
0,4566 |
0,6008 |
0,7530 |
1,4224 |
2,1483 |
2,9086 |
3,6932 |
4,4963 |
5,3143 |
6,1450 |
6,9826 |
|
|
t 2 |
0,8951 |
1,0374 |
1,2808 |
1,5254 |
1,7695 |
2,7638 |
3,7603 |
4,7580 |
5,7561 |
6,7558 |
7,7565 |
8,7582 |
9,7563 |
|
|
t 3 |
2,1030 |
2,3188 |
2,6760 |
3,0230 |
3,3606 |
4,6854 |
5,9544 |
7,1908 |
8,4032 |
9,6011 |
10,7828 |
11,9543 |
13,1133 |
|
|
А |
0,8992 |
0,8969 |
0,8943 |
0,8924 |
0,8910 |
0,8880 |
0,8865 |
0,8857 |
0,8851 |
0,8847 |
0,8844 |
0,8842 |
0,8840 |
|
5 |
t 1 |
0,1814 |
0,2397 |
0,3493 |
0,4702 |
0,6009 |
1,1887 |
1,8439 |
1,8439 |
2,5439 |
3,2734 |
4,0293 |
4,7968 |
5,5778 |
|
|
t 2 |
0,6258 |
0,7412 |
0,9408 |
1,2456 |
1,3552 |
2,2182 |
3,1084 |
3,1084 |
4,0131 |
4,9275 |
5,8543 |
6,7808 |
7,7121 |
|
|
t 3 |
1,3482 |
1,5201 |
1,8053 |
2,0892 |
2,3734 |
3,4899 |
4,5910 |
4,5910, |
5,6816 |
6,7625 |
7,8416 |
8,9114 |
9,9743 |
|
|
t 4 |
2,6117 |
2,8443 |
3,2256 |
3,5998 |
3,9653 |
5,3694 |
6,7061 |
6,7061 |
8,0054 |
9,2782 |
10,5214 |
11,7564 |
12,9657 |
|
|
A |
0,9332 |
0,9315 |
0,9294 |
0,9280 |
0,9269 |
0,9245 |
0,9233 |
0,9233 |
0,9226 |
0,9222 |
0,9219 |
0,9216 |
0,9214 |
|
6 |
t 1 |
0,1397 |
0,1880 |
0,2802 |
0,3846 |
0,4991 |
1,0287 |
1,6324 |
2,2861 |
2,9731 |
3,6884 |
4,4221 |
5,1685 |
5,9306 |
|
|
t 2 |
0,4723 |
0,5687 |
0,7375 |
0,9159 |
1,0989 |
1,8751 |
2,6869 |
3,5271 |
4,3810 |
5,2533 |
6,1283 |
7,0103 |
7,9015 |
|
|
t 3 |
0,9797 |
1,1220 |
1,3614 |
1,6074 |
1,8527 |
2,8453 |
3,8373 |
4,8364 |
5,8320 |
6,8391 |
7,8333 |
8,8296 |
9,8291 |
|
|
t 4 |
1,7436 |
1,9343 |
2,2447 |
2,5606 |
2,8691 |
4,0795 |
5,2552 |
6,4136 |
7,5539 |
8,6922 |
9,8063 |
10,9170 |
12,0216 |
|
|
t 5 |
3,0400 |
3,2810 |
3,6791 |
4,0753 |
4,4615 |
5,9323 |
7,3220 |
8,6669 |
9,9786 |
11,2763 |
12,5327 |
13,7804 |
15,0086 |
|
|
A |
0,9525 |
0,9512 |
0,9496 |
0,9484 |
0,9476 |
0,9456 |
0,9447 |
0,9441 |
0,9437 |
0,9435 |
0,9433 |
0,9432 |
0,9430 |
|
7 |
t 1 |
0,1131 |
0,1535 |
0,2327 |
0,3256 |
0,4289 |
0,9116 |
1,4752 |
1,4752 |
2,0898 |
2,7453 |
3,4230 |
4,1327 |
4,8496 |
|
|
t 2 |
0,3774 |
0,4584 |
0,6042 |
0,7635 |
0,9301 |
1,6347 |
2,3887 |
2,3887 |
3,1734 |
3,9861 |
4,8075 |
5,6502 |
6,4924 |
|
|
t 3 |
0,7654 |
0,8835 |
1,0901 |
1,3105 |
1,5337 |
2,4264 |
3,3424 |
3,3424 |
4,2660 |
5,2083 |
6,1476 |
7,1031 |
8,0461 |
|
|
t 4 |
1,3102 |
1,4654 |
1,7321 |
2,0130 |
2,2901 |
3,3666 |
4,4352 |
4,4352 |
5,4938 |
6,5580 |
7,6079 |
8,6690 |
9,7087 |
|
|
t 5 |
2,1079 |
2,2992 |
2,6297 |
2,9770 |
3,3091 |
4,5805 |
5,8134 |
5,8134 |
7,0140 |
8,2107 |
9,3769 |
10,5512 |
11,6878 |
|
|
t 6 |
3,4340 |
3,6717 |
4,0807 |
4,5037 |
4,8997 |
6,4177 |
7,8427 |
7,8427 |
9,2242 |
10,5817 |
11,8875 |
13,2029 |
14,4619 |
|
|
A |
0,9645 |
0,9634 |
0,9622 |
0,9613 |
0,9606 |
0,9590 |
0,9582 |
0,9582 |
0,9577 |
0,9574 |
0,9572 |
0,9571 |
0,9569 |
|
8 |
t 1 |
0,0928 |
0,1287 |
0,1984 |
0,2806 |
0,3728 |
0,8186 |
1,3521 |
1,9358 |
2,5678 |
3,2212 |
3,8961 |
4,5905 |
5,3113 |
|
|
t 2 |
0,3073 |
0,3808 |
0,5100 |
0,6507 |
0,7986 |
1,4483 |
2,1644 |
2,9061 |
3,6879 |
4,4737 |
5,2738 |
6,0845 |
6,9238 |
|
|
t 3 |
0,6139 |
0,7233 |
0,9067 |
1,0983 |
1,2961 |
2,1198 |
2,9845 |
3,8549 |
4,7574 |
5,6484 |
6,5509 |
7,4522 |
8,3854 |
|
|
t 4 |
1,0279 |
1,1720 |
1,4081 |
1,6492 |
1,8963 |
2,8816 |
3,8846 |
4,8743 |
5,8884 |
6,8772 |
7,8721 |
8,8570 |
9,8751 |
|
|
t 5 |
1,5906 |
1,7692 |
2,0609 |
2,3535 |
2,6486 |
3,7983 |
4,9392 |
6,0508 |
7,1773 |
8,2659 |
9,3493 |
10,4202 |
11,5211 |
|
|
t 6 |
2,3979 |
2,6129 |
2,9689 |
3,3173 |
3,6638 |
4,9957 |
6,2884 |
7,5340 |
8,7777 |
9,9785 |
11,1583 |
12,3244 |
13,5127 |
|
|
t 7 |
3,7311 |
3,9860 |
4,4222 |
4,8452 |
5,2560 |
6,8140 |
8,2993 |
9,7080 |
11,1068 |
12,4460 |
13,7466 |
15,0296 |
16,3311 |
|
|
A |
0,9725 |
0,9716 |
0,9706 |
0,9698 |
0,9693 |
0,9679 |
0,9673 |
0,9669 |
0,9666 |
0,9665 |
0,9663 |
0,9662 |
0,9662 |
|
9 |
t 1 |
0,0787 |
0,1105 |
0,1732 |
0,2468 |
0,3317 |
0,7477 |
1,2542 |
1,2542 |
1,8125 |
2,4090 |
3,0500 |
3,7153 |
4,3829 |
|
|
t 2 |
0,2591 |
0,3247 |
0,4424 |
0,5680 |
0,7048 |
1,3128 |
1,9916 |
1,9916 |
2,6985 |
3,4307 |
4,2015 |
4,9899 |
5,7656 |
|
|
t 3 |
0,5125 |
0,6105 |
0,7786 |
0,9500 |
1,1321 |
1,9002 |
2,7182 |
2,7182 |
3,5447 |
4,3833 |
5,2588 |
6,1427 |
7,0020 |
|
|
t 4 |
0,8458 |
0,9750 |
1,1920 |
1,4057 |
1,6306 |
2,5477 |
3,4928 |
3,4928 |
4,4258 |
5,3630 |
6,3299 |
7,3017 |
8,2363 |
|
|
t 5 |
1,2812 |
1,4412 |
1,7062 |
1,9630 |
2,2298 |
3,2927 |
4,3622 |
4,3622 |
5,3998 |
6,4329 |
7,4887 |
8,5432 |
9,5533 |
|
|
t 6 |
1,8630 |
2,0541 |
2,3699 |
2,6730 |
2,9815 |
4,1986 |
5,3936 |
5,3936 |
6,5420 |
7,6728 |
8,8184 |
9,9642 |
11,0508 |
|
|
t 7 |
2,6943 |
2,9094 |
3,2901 |
3,6410 |
3,9971 |
5,3871 |
6,7224 |
6,7224 |
7,9931 |
9,2315 |
10,4797 |
11,7227 |
12,8984 |
|
|
t 8 |
4,0599 |
4,2886 |
4,7684 |
5,1767 |
5,5918 |
7,1980 |
8,7046 |
8,7046 |
10,1363 |
11,5204 |
12,8944 |
14,2592 |
15,5515 |
|
|
A |
0,9781 |
0,9773 |
0,9765 |
0,9758 |
0,9754 |
0,9742 |
0,9737 |
0,9737 |
0,9734 |
0,9732 |
0,9730 |
0,9729 |
0,9728 |
|
10 |
t 1 |
0,0688 |
0,0954 |
0,1512 |
0,2198 |
0,2986 |
0,6874 |
1,1730 |
1,7117 |
2,2813 |
2,9098 |
3,5438 |
4,2105 |
4,8959 |
|
|
t 2 |
0,2248 |
0,2791 |
0,3834 |
0,5018 |
0,6306 |
1,1971 |
1,8453 |
2,5302 |
3,2241 |
3,9814 |
4,7306 |
5,5070 |
6,2958 |
|
|
t 3 |
0,4410 |
0,5213 |
0,6695 |
0,8323 |
1,0042 |
1,7168 |
2,4972 |
3,2967 |
4,0903 |
4,9485 |
5,7853 |
6,6483 |
7,5161 |
|
|
t 4 |
0,7198 |
0,8247 |
1,0138 |
1,2192 |
1,4307 |
2,2753 |
3,1775 |
4,0800 |
4,9588 |
5,9058 |
6,8241 |
7,7616 |
8,6968 |
|
|
t 5 |
1,0737 |
1,2005 |
1,4309 |
1,6780 |
1,9290 |
2,9025 |
3,9192 |
4,9213 |
5,8812 |
6,9146 |
7,9042 |
8,9150 |
9,9149 |
|
|
t 6 |
1,5258 |
1,6740 |
1,9473 |
2,2374 |
2,5283 |
3,6316 |
4,7651 |
5,8642 |
6,9038 |
8,0252 |
9,0883 |
10,1727 |
11,2369 |
|
|
t 7 |
2,1200 |
2,2914 |
2,6096 |
2,9480 |
3,2830 |
4,5230 |
5,7806 |
6,9823 |
8,1053 |
9,3172 |
10,4638 |
1,6243 |
12,7553 |
|
|
t 8 |
2,9522 |
3,1494 |
3,5210 |
2,9151 |
4,3071 |
5,6989 |
7,0952 |
8,4071 |
9,6315 |
10,9424 |
12,1842 |
13,4376 |
14,6399 |
|
|
t 9 |
4,3042 |
4,5387 |
4,9765 |
5,4556 |
5,9238 |
7,4973 |
9,0832 |
10,5148 |
11,8868 |
13,3275 |
14,6888 |
16,0601 |
17,3658 |
|
|
A |
0,9821 |
0,9815 |
0,9807 |
0,9802 |
0,9798 |
0,9789 |
0,9784 |
0,9781 |
0,9779 |
0,9778 |
0,9777 |
0,9776 |
0,9776 |
Таблица A.56 - Оптимальные вероятности (частоты) интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного параметра гамма-распределения и известных значениях основного параметра θ0) и соответствующие значения относительной асимптотической информации А
|
k |
Pi |
θ 0 |
||||||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
2 |
P 1 |
0,9604 |
0,9149 |
0,8617 |
0,8245 |
0,7968 |
0,7306 |
0,6951 |
0,6723 |
0,6559 |
0,6433 |
0,6335 |
0,6254 |
0,6187 |
|
|
P 2 |
0,0396 |
0,0851 |
0,1383 |
0,1755 |
0,2032 |
0,2694 |
0,3049 |
0,3277 |
0,3441 |
0,3567 |
0,3665 |
0,3746 |
0,3813 |
|
3 |
P 1 |
0,9242 |
0,8401 |
0,7458 |
0,6832 |
0,6386 |
0,5385 |
0,4894 |
0,2708 |
0,2709 |
0,2708 |
0,2709 |
0,2708 |
0,2708 |
|
|
P 2 |
0,0641 |
0,1335 |
0,2083 |
0,2556 |
0,2880 |
0,3551 |
0,3844 |
0,4616 |
0,4612 |
0,4608 |
0,4606 |
0,4605 |
0,4604 |
|
|
P 3 |
0,0116 |
0,0264 |
0,0460 |
0,0612 |
0,0734 |
0,1064 |
0,1262 |
0,2676 |
0,2680 |
0,2684 |
0,2684 |
0,2687 |
0,2688 |
|
4 |
P 1 |
0,8956 |
0,7825 |
0,6607 |
0,5831 |
0,5290 |
0,4159 |
0,3634 |
0,3323 |
0,3115 |
0,2964 |
0,2851 |
0,2762 |
0,2686 |
|
|
P 2 |
0,0758 |
0,1532 |
0,2298 |
0,2734 |
0,3005 |
0,3468 |
0,3612 |
0,3670 |
0,3695 |
0,3706 |
0,3709 |
0,3708 |
0,3704 |
|
|
P 3 |
0,0237 |
0,0527 |
0,0888 |
0,1152 |
0,1357 |
0,1848 |
0,2113 |
0,2283 |
0,2403 |
0,2492 |
0,2560 |
0,2614 |
0,2662 |
|
|
P 4 |
0,0049 |
0,0115 |
0,0207 |
0,0283 |
0,0347 |
0,0525 |
0,0640 |
0,0723 |
0,0788 |
0,0838 |
0,0880 |
0,0915 |
0,0947 |
|
5 |
P 1 |
0,8722 |
0,7373 |
0,5967 |
0,5100 |
0,4517 |
0,3333 |
0,2812 |
0,1159 |
0,1148 |
0,1139 |
0,1137 |
0,1130 |
0,1124 |
|
|
P 2 |
0,0819 |
0,1612 |
0,2331 |
0,2700 |
0,2904 |
0,3166 |
0,3195 |
0,2612 |
0,2590 |
0,2574 |
0,2566 |
0,2556 |
0,2550 |
|
|
P 3 |
0,0317 |
0,0690 |
0,1127 |
0,1429 |
0,1647 |
0,2132 |
0,2357 |
0,2958 |
0,2963 |
0,2966 |
0,2966 |
0,2970 |
0,2969 |
|
|
P 4 |
0,0116 |
0,0265 |
0,0463 |
0,0619 |
0,0742 |
0,1073 |
0,1267 |
0,2287 |
0,2306 |
0,2323 |
0,2326 |
0,2337 |
0,2344 |
|
|
P 5 |
0,0026 |
0,0060 |
0,0111 |
0,0153 |
0,0190 |
0,0297 |
0,0369 |
0,0984 |
0,0993 |
0,0998 |
0,1005 |
0,1007 |
0,1013 |
|
6 |
P 1 |
0,8528 |
0,7005 |
0,5459 |
0,4536 |
0,3929 |
0,2748 |
0,2250 |
0,1978 |
0,1802 |
0,1683 |
0,1591 |
0,1516 |
0,1457 |
|
|
P 2 |
0,0852 |
0,1638 |
0,2295 |
0,2598 |
0,2738 |
0,2843 |
0,2781 |
0,2714 |
0,2649 |
0,2601 |
0,2552 |
0,2513 |
0,2480 |
|
|
P 3 |
0,0371 |
0,0790 |
0,1256 |
0,1557 |
0,1764 |
0,2174 |
0,2339 |
0,2421 |
0,2467 |
0,2499 |
0,2515 |
0,2530 |
0,2539 |
|
|
P 4 |
0,0169 |
0,0379 |
0,0648 |
0,0846 |
0,1001 |
0,1376 |
0,1582 |
0,1708 |
0,1800 |
0,1860 |
0,1913 |
0,1956 |
0,1988 |
|
|
P 5 |
0,0066 |
0,0152 |
0,0274 |
0,0371 |
0,0452 |
0,0675 |
0,0815 |
0,0911 |
0,0985 |
0,1039 |
0,1089 |
0,1130 |
0,1163 |
|
|
P 6 |
0,0015 |
0,0036 |
0,0067 |
0,0093 |
0,0115 |
0,0184 |
0,0232 |
0,0268 |
0,0297 |
0,0318 |
0,0339 |
0,0357 |
0,0373 |
|
7 |
P 1 |
0,8368 |
0,6702 |
0,5049 |
0,4098 |
0,3488 |
0,2318 |
0,1850 |
0,0626 |
0,0611 |
0,0604 |
0,0595 |
0,0594 |
0,0587 |
|
|
P 2 |
0,0870 |
0,1639 |
0,2235 |
0,2473 |
0,2567 |
0,2544 |
0,2424 |
0,1564 |
0,1535 |
0,1523 |
0,1507 |
0,1500 |
0,1488 |
|
|
P 3 |
0,0405 |
0,0848 |
0,1319 |
0,1603 |
0,1788 |
0,2111 |
0,2217 |
0,2101 |
0,2083 |
0,2078 |
0,2071 |
0,2072 |
0,2064 |
|
|
P 4 |
0,0207 |
0,0460 |
0,0771 |
0,0987 |
0,1145 |
0,1521 |
0,1700 |
0,2176 |
0,2185 |
0,2188 |
0,2190 |
0,2193 |
0,2196 |
|
|
P 5 |
0,0101 |
0,0232 |
0,0409 |
0,0542 |
0,0647 |
0,0935 |
0,1102 |
0,1847 |
0,1868 |
0,1880 |
0,1890 |
0,1895 |
0,1900 |
|
|
P 6 |
0,0040 |
0,0096 |
0,0175 |
0,0238 |
0,0291 |
0,0451 |
0,0553 |
0,1215 |
0,1239 |
0,1247 |
0,1258 |
0,1260 |
0,1272 |
|
|
P 7 |
0,0009 |
0,0023 |
0,0043 |
0,0059 |
0,0074 |
0,0121 |
0,0155 |
0,0471 |
0,0479 |
0,0480 |
0,0488 |
0,0486 |
0,0493 |
|
8 |
P 1 |
0,8219 |
0,6444 |
0,4713 |
0,3733 |
0,3112 |
0,1979 |
0,1550 |
0,1315 |
0,1181 |
0,1078 |
0,1001 |
0,0942 |
0,0903 |
|
|
P 2 |
0,0881 |
0,1627 |
0,2162 |
0,2343 |
0,2388 |
0,2268 |
0,2127 |
0,2003 |
0,1924 |
0,1847 |
0,1787 |
0,1735 |
0,1707 |
|
|
P 3 |
0,0431 |
0,0884 |
0,1344 |
0,1602 |
0,1764 |
0,2007 |
0,2056 |
0,2059 |
0,2055 |
0,2037 |
0,2026 |
0,2006 |
0,2001 |
|
|
P 4 |
0,0238 |
0,0517 |
0,0848 |
0,1072 |
0,1235 |
0,1570 |
0,1712 |
0,1792 |
0,1838 |
0,1870 |
0,1893 |
0,1907 |
0,1919 |
|
|
P 5 |
0,0131 |
0,0295 |
0,0510 |
0,0671 |
0,0794 |
0,1100 |
0,1256 |
0,1364 |
0,1428 |
0,1486 |
0,1525 |
0,1562 |
0,1581 |
|
|
P 6 |
0,0066 |
0,0153 |
0,0275 |
0,0373 |
0,0451 |
0,0670 |
0,0796 |
0,0889 |
0,0945 |
0,1002 |
0,1044 |
0,1085 |
0,1105 |
|
|
P 7 |
0,0027 |
0,0064 |
0,0119 |
0,0165 |
0,0204 |
0,0320 |
0,0394 |
0,0451 |
0,0489 |
0,0526 |
0,0557 |
0,0586 |
0,0602 |
|
|
P 8 |
0,0006 |
0,0016 |
0,0029 |
0,0041 |
0,0052 |
0,0086 |
0,0109 |
0,0128 |
0,0141 |
0,0153 |
0,0166 |
0,0177 |
0,0183 |
|
9 |
P 1 |
0,8095 |
0,6225 |
0,4438 |
0,3437 |
0,2823 |
0,1725 |
0,1325 |
0,0387 |
0,0373 |
0,0362 |
0,0361 |
0,0360 |
0,0351 |
|
|
P 2 |
0,0886 |
0,1608 |
0,2093 |
0,2223 |
0,2235 |
0,2052 |
0,1886 |
0,1027 |
0,0996 |
0,0971 |
0,0966 |
0,0964 |
0,0945 |
|
|
P 3 |
0,0448 |
0,0905 |
0,1348 |
0,1585 |
0,1719 |
0,1886 |
0,1898 |
0,1486 |
0,1462 |
0,1439 |
0,1438 |
0,1436 |
0,1416 |
|
|
P 4 |
0,0261 |
0,0557 |
0,0895 |
0,1115 |
0,1265 |
0,1560 |
0,1670 |
0,1719 |
0,1707 |
0,1702 |
0,1700 |
0,1703 |
0,1692 |
|
|
P 5 |
0,0155 |
0,0343 |
0,0579 |
0,0754 |
0,0883 |
0,1182 |
0,1325 |
0,1721 |
0,1729 |
0,1737 |
0,1738 |
0,1738 |
0,1743 |
|
|
P 6 |
0,0088 |
0,0201 |
0,0352 |
0,0475 |
0,0568 |
0,0814 |
0,0945 |
0,1520 |
0,1543 |
0,1558 |
0,1559 |
0,1566 |
0,1578 |
|
|
P 7 |
0,0045 |
0,0105 |
0,0192 |
0,0264 |
0,0323 |
0,0488 |
0,0587 |
0,1166 |
0,1190 |
0,1207 |
0,1211 |
0,1211 |
0,1230 |
|
|
P 8 |
0,0019 |
0,0045 |
0,0083 |
0,0117 |
0,0146 |
0,0231 |
0,0286 |
0,0713 |
0,0733 |
0,0750 |
0,0751 |
0,0749 |
0,0765 |
|
|
P 9 |
0,0004 |
0,0011 |
0,0020 |
0,0029 |
0,0037 |
0,0061 |
0?0079 |
0,0261 |
0,0268 |
0,0274 |
0,0275 |
0,0274 |
0,0280 |
|
10 |
P 1 |
0,7994 |
0,6018 |
0,4176 |
0,3186 |
0,2581 |
0,1514 |
0,1147 |
0,0949 |
0,0816 |
0,0751 |
0,0687 |
0,0647 |
0,0615 |
|
|
P 2 |
0,0886 |
0,1586 |
0,2012 |
0,2104 |
0,2096 |
0,1849 |
0,1668 |
0,1540 |
0,1421 |
0,1369 |
0,1309 |
0,1267 |
0,1232 |
|
|
P 3 |
0,0458 |
0,0919 |
0,1340 |
0,1549 |
0,1659 |
0,1756 |
0,1739 |
0,1700 |
0,1651 |
0,1630 |
0,1597 |
0,1577 |
0,1555 |
|
|
P 4 |
0,0276 |
0,0588 |
0,0927 |
0,1137 |
0,1272 |
0,1515 |
0,1599 |
0,1631 |
0,1634 |
0,1641 |
0,1645 |
0,1643 |
0,1635 |
|
|
P 5 |
0,0172 |
0,0381 |
0,0638 |
0,0812 |
0,0938 |
0,1224 |
0,1344 |
0,1418 |
0,1465 |
0,1492 |
0,1510 |
0,1528 |
0,1537 |
|
|
P 6 |
0,0105 |
0,0242 |
0,0423 |
0,0554 |
0,0655 |
0,0916 |
0,1043 |
0,1125 |
0,1193 |
0,1228 |
0,1264 |
0,1289 |
0,1309 |
|
|
P 7 |
0,0061 |
0,0145 |
0,0261 |
0,0351 |
0,0423 |
0,0627 |
0,0734 |
0,0810 |
0,0882 |
0,0912 |
0,0954 |
0,0978 |
0,1001 |
|
|
P 8 |
0,0032 |
0,0078 |
0,0144 |
0,0196 |
0,0240 |
0,0375 |
0,0449 |
0,0506 |
0,0567 |
0,0589 |
0,0622 |
0,0644 |
0,0664 |
|
|
P 9 |
0,0013 |
0,0034 |
0,0064 |
0,0088 |
0,0108 |
0,0177 |
0,0218 |
0,0250 |
0,0288 |
0,0302 |
0,0321 |
0,0332 |
0,0348 |
|
|
P 10 |
0,0003 |
0,0008 |
0,0016 |
0,0022 |
0,0027 |
0,0047 |
0,0058 |
0,0071 |
0,0082 |
0,0087 |
0,0093 |
0,0096 |
0,0102 |
Таблица A.57 - Оптимальные граничные точки интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного и основного параметров гамма-распределения в зависимости от значений основного параметра θ0) и соответствующие значения относительной асимптотической информации А
|
k |
ti |
θ 0 |
||||||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
3 |
t 1 |
0,0002 |
0,0001 |
0,0174 |
0,0674 |
0,1465 |
0,6326 |
1,2531 |
1,9397 |
2,6678 |
3,4243 |
4,1991 |
5,0000 |
5,5684 |
|
|
t 2 |
0,7690 |
1,3001 |
1,3958 |
1,7831 |
2,1616 |
3,6024 |
4,9530 |
6,2482 |
7,5171 |
8,7554 |
9,9722 |
11,0000 |
11,5683 |
|
|
А |
0,2935 |
0,4295 |
0,4235 |
0,4191 |
0,4160 |
0,4108 |
0,4090 |
0,4082 |
0,4078 |
0,4076 |
0,4074 |
0,4066 |
0,3959 |
|
4 |
t 1 |
0,0001 |
0,0009 |
0,0141 |
0,0547 |
0,1192 |
0,5255 |
1,0651 |
1,6535 |
2,3099 |
3,0485 |
3,8332 |
4,4721 |
5,1905 |
|
|
t 2 |
0,1050 |
0,4420 |
0,7205 |
0,9295 |
1,1408 |
2,0195 |
2,9542 |
3,7846 |
4,7349 |
5,9786 |
7,0038 |
7,7331 |
8,5822 |
|
|
t 3 |
1,0554 |
1,6647 |
2,1525 |
2,5459 |
2,9273 |
4,3900 |
5,7928 |
7,0557 |
8,3627 |
9,8297 |
11,0038 |
12,1919 |
13,3510 |
|
|
А |
0,3907 |
0,5375 |
0,5533 |
0,5528 |
0,5522 |
0,5519 |
0,5516 |
0,5518 |
0,5520 |
0,5519 |
0,5518 |
0,5522 |
0,5522 |
|
5 |
t 1 |
0,0001 |
0,0001 |
0,0022 |
0,0163 |
0,0489 |
0,3372 |
0,7833 |
1,3162 |
1,9088 |
2,5400 |
3,2076 |
3,8879 |
4,5914 |
|
|
t 2 |
0,0067 |
0,0069 |
0,0562 |
0,1567 |
0,2866 |
0,9477 |
1,7049 |
2,5067 |
3,3384 |
4,1833 |
5,0516 |
5,9108 |
6,7911 |
|
|
t 3 |
0,4719 |
0,4976 |
0,9018 |
1,2211 |
1,5380 |
2,7990 |
4,0007 |
5,1861 |
6,3503 |
7,4937 |
8,6378 |
9,7492 |
10,8738 |
|
|
t 4 |
1,6365 |
1,7707 |
2,3241 |
2,8083 |
3,2629 |
4,9736 |
6,4906 |
7,9494 |
9,3623 |
10,7201 |
12,0696 |
13,3731 |
14,6632 |
|
|
A |
0,4606 |
0,6722 |
0,6873 |
0,6863 |
0,6854 |
0,6843 |
0,6831 |
0,6829 |
0,6828 |
0,6827 |
0,6827 |
0,6827 |
0,6827 |
|
6 |
t 1 |
0,0001 |
0,0001 |
0,0015 |
0,0117 |
0,0359 |
0,2749 |
0,6666 |
1,1605 |
1,7122 |
2,3025 |
2,4947 |
3,5934 |
4,2563 |
|
|
t 2 |
0,0084 |
0,0081 |
0,0395 |
0,1075 |
0,1994 |
0,7283 |
1,3734 |
2,0974 |
2,8583 |
3,6306 |
4,4208 |
5,2755 |
6,0669 |
|
|
t 3 |
0,3965 |
0,4143 |
0,5026 |
0,6546 |
0,8360 |
1,7532 |
2,6992 |
3,7061 |
4,7238 |
5,7019 |
6,6737 |
7,7638 |
8,6866 |
|
|
t 4 |
1,0052 |
1,1842 |
1,4058 |
1,7072 |
2,0307 |
3,3927 |
4,6776 |
5,9657 |
7,2088 |
8,4152 |
9,5909 |
10,8271 |
11,9504 |
|
|
t 5 |
2,1652 |
2,4989 |
2,8500 |
3,2836 |
3,7235 |
5,4747 |
7,0410 |
8,5901 |
10,0180 |
11,4056 |
12,7849 |
14,1612 |
15,4369 |
|
|
A |
0,4971 |
0,7353 |
0,7537 |
0,7547 |
0,7550 |
0,7562 |
0,7552 |
0,7553 |
0,7553 |
0,7554 |
0,7554 |
0,7554 |
0,7554 |
|
7 |
t 1 |
0,0001 |
0,0001 |
0,0004 |
0,0057 |
0,0221 |
0,2167 |
0,5653 |
1,0141 |
1,5232 |
2,0821 |
2,6677 |
3,2932 |
3,9406 |
|
|
t 2 |
0,0038 |
0,0025 |
0,0108 |
0,0500 |
0,1166 |
0,5478 |
1,1131 |
1,7702 |
2,4536 |
3,1743 |
3,9123 |
4,6777 |
5,4648 |
|
|
t 3 |
0,1797 |
0,0410 |
0,0925 |
0,2284 |
0,3912 |
1,1407 |
1,9393 |
2,8270 |
3,6910 |
4,5783 |
5,4600 |
6,3671 |
7,3013 |
|
|
t 4 |
0,5288 |
0,4646 |
0,6828 |
0,9915 |
1,2954 |
2,4686 |
3,5748 |
4,7415 |
5,8355 |
6,9445 |
8,0213 |
9,1131 |
10,2077 |
|
|
t 5 |
1,0436 |
1,1561 |
1,5670 |
2,0188 |
2,4198 |
3,9694 |
5,3077 |
6,6860 |
7,9718 |
9,2499 |
10,4796 |
11,7240 |
12,9476 |
|
|
t 6 |
2,2397 |
2,4021 |
2,9833 |
3,5832 |
4,0461 |
5,9991 |
7,5653 |
9,1629 |
10,6299 |
12,0854 |
13,4560 |
14,8718 |
16,2321 |
|
|
A |
0,5114 |
0,7667 |
0,8105 |
0,8109 |
0,8108 |
0,8119 |
0,8102 |
0,8102 |
0,8102 |
0,8102 |
0,8102 |
0,8102 |
0,8102 |
|
8 |
t 1 |
0,0001 |
0,0001 |
0,0003 |
0,0040 |
0,0159 |
0,1844 |
0,4977 |
0,9170 |
1,3943 |
1,9240 |
2,5077 |
3,0919 |
3,7563 |
|
|
t 2 |
0,0027 |
0,0022 |
0,0084 |
0,0348 |
0,0826 |
0,4551 |
0,9594 |
1,5625 |
2,2038 |
2,8839 |
3,6103 |
4,3191 |
5,1373 |
|
|
t 3 |
0,0957 |
0,0328 |
0,0705 |
0,1502 |
0,2602 |
0,8978 |
1,5950 |
2,3867 |
3,1820 |
4,0075 |
4,8728 |
5,6906 |
6,6741 |
|
|
t 4 |
0,3263 |
0,3834 |
0,4798 |
0,5781 |
0,7609 |
1,7715 |
2,6854 |
2,7086 |
4,6920 |
5,6847 |
6,7305 |
7,6677 |
8,9040 |
|
|
t 5 |
0,6101 |
0,9448 |
1,1839 |
1,3564 |
1,6561 |
3,0194 |
4,1947 |
5,4260 |
6,6012 |
7,7777 |
8,9631 |
10,0664 |
11,4006 |
|
|
t 6 |
1,2780 |
1,7712 |
2,1530 |
2,3744 |
2,7596 |
4,4362 |
5,8189 |
7,2285 |
8,5823 |
9,8976 |
11,2079 |
12,4406 |
13,8668 |
|
|
t 7 |
2,3017 |
3,1466 |
3,6705 |
3,9163 |
4,4165 |
6,4500 |
8,0196 |
9,6521 |
11,1743 |
12,6288 |
14,0809 |
15,4715 |
16,9779 |
|
|
A |
0,5196 |
0,7959 |
0,8453 |
0,8468 |
0,8470 |
0,8491 |
0,8471 |
0,8472 |
0,8472 |
0,8472 |
0,8472 |
0,8472 |
0,8471 |
|
9 |
t 1 |
0,0001 |
0,0001 |
0,0002 |
0,0022 |
0,0117 |
0,1574 |
0,4415 |
0,8250 |
1,2787 |
1,8036 |
2,3310 |
2,9325 |
3,5049 |
|
|
t 2 |
0,0036 |
0,0018 |
0,0037 |
0,0189 |
0,0595 |
0,3801 |
0,8363 |
1,3799 |
1,9839 |
2,6636 |
3,3046 |
4,0472 |
4,7203 |
|
|
t 3 |
0,1629 |
0,0233 |
0,0294 |
0,0782 |
0,1800 |
0,7206 |
1,3446 |
2,0408 |
2,7845 |
3,6131 |
4,3498 |
5,2235 |
5,9677 |
|
|
t 4 |
0,4542 |
0,2630 |
0,1561 |
0,2537 |
0,4663 |
1,3046 |
2,1024 |
2,9543 |
3,8605 |
4,8731 |
5,6929 |
6,7298 |
7,5272 |
|
|
t 5 |
0,8449 |
0,6803 |
0,7006 |
0,8015 |
1,1711 |
2,3623 |
3,3756 |
4,4160 |
5,5171 |
6,7275 |
7,6700 |
8,8737 |
9,8149 |
|
|
t 6 |
1,3601 |
1,2444 |
1,4308 |
1,5324 |
2,0444 |
3,5295 |
4,7341 |
5,9506 |
7,2053 |
8,5518 |
9,6244 |
10,9257 |
11,9962 |
|
|
t 7 |
2,0236 |
2,0557 |
2,4709 |
2,4940 |
3,1377 |
4,8994 |
6,2737 |
7,6705 |
9,0544 |
10,5335 |
11,7263 |
13,1211 |
14,3026 |
|
|
t 8 |
3,2912 |
3,3968 |
4,0759 |
3,9852 |
4,7460 |
6,9403 |
8,4320 |
9,9701 |
11,5363 |
13,1888 |
14,4967 |
15,9995 |
17,3478 |
|
|
A |
0,5331 |
0,8132 |
0,8731 |
0,8746 |
0,8752 |
0,8777 |
0,8750 |
0,8751 |
0,8751 |
0,8751 |
0,8752 |
0,8751 |
0,8752 |
|
10 |
t 1 |
0,0001 |
0,0001 |
0,0001 |
0,0017 |
0,0088 |
0,1354 |
0,4037 |
0,7710 |
1,2056 |
1,7008 |
2,2056 |
2,7623 |
3,3874 |
|
|
t 2 |
0,0014 |
0,0011 |
0,0015 |
0,0148 |
0,0445 |
0,3236 |
0,7554 |
1,2761 |
1,8522 |
2,4850 |
3,1019 |
3,7698 |
4,5270 |
|
|
t 3 |
0,0258 |
0,0105 |
0,0114 |
0,0599 |
0,1314 |
0,5997 |
1,1925 |
1,8495 |
2,5594 |
3,3033 |
4,0198 |
4,7890 |
5,6411 |
|
|
t 4 |
0,1769 |
0,0813 |
0,0537 |
0,1839 |
0,3195 |
1,0272 |
1,7976 |
2,6008 |
3,4385 |
4,3011 |
5,1228 |
5,9921 |
6,9987 |
|
|
t 5 |
0,4189 |
0,3690 |
0,2154 |
0,5363 |
0,7622 |
1,7846 |
2,7624 |
3,7386 |
4,7390 |
5,7567 |
6,6818 |
7,6452 |
8,7656 |
|
|
t 6 |
0,7642 |
0,7764 |
0,6807 |
1,1571 |
1,4768 |
2,7934 |
3,9800 |
5,1491 |
6,3872 |
7,4632 |
8,5358 |
9,6020 |
10,8348 |
|
|
t 7 |
1,2344 |
1,3290 |
1,3022 |
1,9077 |
2,3108 |
3,8955 |
5,2602 |
6,5860 |
7,9069 |
9,1388 |
10,3168 |
11,5153 |
12,8376 |
|
|
t 8 |
1,9812 |
2,1251 |
2,1657 |
2,9083 |
3,3819 |
5,2597 |
6,7736 |
8,2430 |
9,6771 |
10,0173 |
12,3097 |
13,6369 |
15,0781 |
|
|
t 9 |
3,1510 |
3,4573 |
3,5785 |
4,4672 |
5,0088 |
7,3134 |
8,9003 |
10,5600 |
12,2411 |
13,5436 |
15,0178 |
16,4962 |
18,0356 |
|
|
A |
0,5362 |
0,8245 |
0,8936 |
0,8956 |
0,8958 |
0,8990 |
0,8957 |
0,8958 |
0,8956 |
0,8958 |
0,8959 |
0,8959 |
0,8959 |
Таблица A.58 - Оптимальные вероятности (частоты) интервалов группирования при проверке сложных гипотез по критериям типа χ2 (при оценивании масштабного и основного параметров гамма-распределения в зависимости от значений основного параметра θ0) и соответствующие значения относительной асимптотической информации А
|
k |
Pi |
θ 0 |
||||||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
3 |
P 1 |
0,1085 |
0,1103 |
0,1480 |
0,1399 |
0,1363 |
0,1327 |
0,1322 |
0,1322 |
0,1323 |
0,1325 |
0,1324 |
0,1334 |
0,1115 |
|
|
P 2 |
0,8260 |
0,8157 |
0,7573 |
0,7523 |
0,7486 |
0,7418 |
0,7391 |
0,7374 |
0,7368 |
0,7361 |
0,7357 |
0,7234 |
0,7031 |
|
|
P 3 |
0,0655 |
0,0740 |
0,0947 |
0,1079 |
0,1151 |
0,1255 |
0,1287 |
0,1304 |
0,1308 |
0,1314 |
0,1319 |
0,1432 |
0,1854 |
|
4 |
P 1 |
0,4173 |
0,1911 |
0,1334 |
0,1202 |
0,1124 |
0,0980 |
0,0927 |
0,0864 |
0,0849 |
0,0889 |
0,0940 |
0,0843 |
0,0812 |
|
|
P 2 |
0,4352 |
0,6429 |
0,6366 |
0,5976 |
0,5681 |
0,5012 |
0,4738 |
0,4370 |
0,4269 |
0,4620 |
0,4568 |
0,4249 |
0,4069 |
|
|
P 3 |
0,1254 |
0,1423 |
0,1920 |
0,2351 |
0,2660 |
0,3339 |
0,3617 |
0,3977 |
0,4075 |
0,3753 |
0,3707 |
0,4093 |
0,4271 |
|
|
P 4 |
0,0221 |
0,0237 |
0,0380 |
0,0471 |
0,0535 |
0,0668 |
0,0719 |
0,0789 |
0,0807 |
0,0738 |
0,0785 |
0,0815 |
0,0848 |
|
5 |
P 1 |
0,4185 |
0,1103 |
0,0528 |
0,0493 |
0,0477 |
0,0456 |
0,0451 |
0,0447 |
0,0448 |
0,0447 |
0,0451 |
0,0447 |
0,0446 |
|
|
P 2 |
0,2184 |
0,2072 |
0,2097 |
0,2044 |
0,2015 |
0,1995 |
0,1990 |
0,1991 |
0,1996 |
0,1994 |
0,2003 |
0,1991 |
0,1995 |
|
|
P 3 |
0,3012 |
0,5283 |
0,5582 |
0,5444 |
0,5360 |
0,5237 |
0,5179 |
0,5163 |
0,5147 |
0,5137 |
0,5128 |
0,5125 |
0,5125 |
|
|
P 4 |
0,0526 |
0,1309 |
0,1482 |
0,1664 |
0,1765 |
0,1899 |
0,1947 |
0,1960 |
0,1970 |
0,1978 |
0,1977 |
0,1993 |
0,1989 |
|
|
P 5 |
0,0093 |
0,0233 |
0,0311 |
0,0355 |
0,0383 |
0,0413 |
0,0433 |
0,0439 |
0,0439 |
0,0443 |
0,0441 |
0,0444 |
0,0445 |
|
6 |
P 1 |
0,4184 |
0,1103 |
0,0437 |
0,0385 |
0,0353 |
0,0315 |
0,0302 |
0,0304 |
0,0304 |
0,0301 |
0,0299 |
0,0305 |
0,0300 |
|
|
P 2 |
0,2328 |
0,2201 |
0,1777 |
0,1567 |
0,1455 |
0,1342 |
0,1299 |
0,1304 |
0,1311 |
0,1300 |
0,1291 |
0,1332 |
0,1297 |
|
|
P 3 |
0,2757 |
0,4891 |
0,4626 |
0,4142 |
0,3858 |
0,3574 |
0,3461 |
0,3463 |
0,3483 |
0,3452 |
0,3417 |
0,3499 |
0,3427 |
|
|
P 4 |
0,0491 |
0,1286 |
0,2225 |
0,2733 |
0,3022 |
0,3292 |
0,3393 |
0,3386 |
0,3354 |
0,3386 |
0,3413 |
0,3317 |
0,3393 |
|
|
P 5 |
0,0194 |
0,0427 |
0,0766 |
0,0959 |
0,1071 |
0,1205 |
0,1258 |
0,1260 |
0,1259 |
0,1267 |
0,1288 |
0,1258 |
0,1285 |
|
|
P 6 |
0,0046 |
0,0092 |
0,0170 |
0,0214 |
0,0241 |
0,0271 |
0,0287 |
0,0283 |
0,0289 |
0,0294 |
0,0293 |
0,0289 |
0,0298 |
|
7 |
P 1 |
0,4185 |
0,1103 |
0,0226 |
0,0225 |
0,0219 |
0,0203 |
0,0198 |
0,0199 |
0,0197 |
0,0197 |
0,0194 |
0,0196 |
0,0196 |
|
|
P 2 |
0,1834 |
0,1362 |
0,0943 |
0,0901 |
0,0882 |
0,0847 |
0,0824 |
0,0841 |
0,0830 |
0,0828 |
0,0823 |
0,0824 |
0,0830 |
|
|
P 3 |
0,2697 |
0,2459 |
0,2160 |
0,2141 |
0,2137 |
0,2108 |
0,2047 |
0,2101 |
0,2083 |
0,2080 |
0,2060 |
0,2060 |
0,2083 |
|
|
P 4 |
0,0732 |
0,3436 |
0,4245 |
0,4107 |
0,4025 |
0,3904 |
0,3859 |
0,3827 |
0,3813 |
0,3816 |
0,3815 |
0,3813 |
0,3791 |
|
|
P 5 |
0,0328 |
0,1099 |
0,1659 |
0,1793 |
0,1848 |
0,2000 |
0,2062 |
0,2035 |
0,2064 |
0,2065 |
0,2081 |
0,2085 |
0,2077 |
|
|
P 6 |
0,0184 |
0,0436 |
0,0621 |
0,0677 |
0,0714 |
0,0765 |
0,0818 |
0,0808 |
0,0819 |
0,0821 |
0,0829 |
0,0829 |
0,0828 |
|
|
P 7 |
0,0041 |
0,0104 |
0,0146 |
0,0156 |
0,0175 |
0,0174 |
0,0193 |
0,0189 |
0,0194 |
0,0193 |
0,0198 |
0,0194 |
0,0194 |
|
8 |
P 1 |
0,4185 |
0,1103 |
0,0195 |
0,0173 |
0,0158 |
0,0150 |
0,0142 |
0,0143 |
0,0140 |
0,0140 |
0,0144 |
0,0140 |
0,0150 |
|
|
P 2 |
0,1632 |
0,1285 |
0,0836 |
0,0691 |
0,0635 |
0,0619 |
0,0588 |
0,0594 |
0,0589 |
0,0587 |
0,0597 |
0,0584 |
0,0625 |
|
|
P 3 |
0,2425 |
0,2276 |
0,1896 |
0,1600 |
0,1498 |
0,1498 |
0,1424 |
0,1448 |
0,1433 |
0,1434 |
0,1453 |
0,1422 |
0,1521 |
|
|
P 4 |
0,0899 |
0,3416 |
0,3800 |
0,3250 |
0,3037 |
0,3019 |
0,2874 |
0,2891 |
0,2877 |
0,2864 |
0,2899 |
0,2851 |
0,3021 |
|
|
P 5 |
0,0386 |
0,1181 |
0,2034 |
0,2553 |
0,2764 |
0,2751 |
0,2863 |
0,2821 |
0,2835 |
0,2851 |
0,2804 |
0,2859 |
0,2700 |
|
|
P 6 |
0,0316 |
0,0505 |
0,0859 |
0,1167 |
0,1276 |
0,1319 |
0,1404 |
0,1396 |
0,1418 |
0,1414 |
0,1397 |
0,1424 |
0,1321 |
|
|
P 7 |
0,0119 |
0,0191 |
0,0312 |
0,0457 |
0,0512 |
0,0526 |
0,0570 |
0,0570 |
0,0574 |
0,0574 |
0,0569 |
0,0583 |
0,0535 |
|
|
P 8 |
0,0038 |
0,0042 |
0,0067 |
0,0110 |
0,0121 |
0,0118 |
0,0135 |
0,0136 |
0,0134 |
0,0136 |
0,0135 |
0,0137 |
0,0128 |
|
9 |
P 1 |
0,4185 |
0,1103 |
0,0160 |
0,0110 |
0,0116 |
0,0112 |
0,0103 |
0,0101 |
0,0100 |
0,0105 |
0,0100 |
0,0105 |
0,0100 |
|
|
P 2 |
0,1802 |
0,1168 |
0,0526 |
0,0440 |
0,0461 |
0,0451 |
0,0424 |
0,0414 |
0,0412 |
0,434 |
0,0413 |
0,0435 |
0,0414 |
|
|
P 3 |
0,2656 |
0,2019 |
0,1230 |
0,1006 |
0,1070 |
0,1067 |
0,1005 |
0,0988 |
0,0987 |
0,1038 |
0,0989 |
0,1037 |
0,0981 |
|
|
P 4 |
0,0713 |
0,3223 |
0,2321 |
0,1942 |
0,2080 |
0,2118 |
0,1977 |
0,1922 |
0,1940 |
0,2041 |
0,1943 |
0,2034 |
0,1923 |
|
|
P 5 |
0,0333 |
0,1365 |
0,3398 |
0,3223 |
0,3173 |
0,3085 |
0,3045 |
0,3008 |
0,3012 |
0,3014 |
03002 |
0,3000 |
0,3042 |
|
|
P 6 |
0,0172 |
0,0645 |
0,1458 |
0,1854 |
0,1806 |
0,1839 |
0,1956 |
0,2010 |
0,1998 |
0,1911 |
0,1997 |
0,1908 |
0,1988 |
|
|
P 7 |
0,0084 |
0,0315 |
0,0645 |
0,0926 |
0,0861 |
0,0888 |
0,0981 |
0,1028 |
0,1019 |
0,0963 |
0,1024 |
0,0973 |
0,1019 |
|
|
P 8 |
0,0044 |
0,0130 |
0,0219 |
0,0396 |
0,0347 |
0,0363 |
0,0410 |
0,0423 |
0,0427 |
0,0399 |
0,0428 |
0,0407 |
0,0431 |
|
|
P 9 |
0,0011 |
0,0031 |
0,0043 |
0,0102 |
0,0087 |
0,0077 |
0,0098 |
0,0106 |
0,0105 |
0,0095 |
0,0105 |
0,0100 |
0,0103 |
|
10 |
P 1 |
0,4185 |
0,1103 |
0,0113 |
0,0091 |
0,0088 |
0,0084 |
0,0081 |
0,0080 |
0,0079 |
0,0080 |
0,0076 |
0,0075 |
0,0081 |
|
|
P 2 |
0,1263 |
0,0906 |
0,0324 |
0,0368 |
0,0348 |
0,0339 |
0,0331 |
0,0327 |
0,0324 |
0,0330 |
0,0314 |
0,0311 |
0,0334 |
|
|
P 3 |
0,1827 |
0,1515 |
0,0763 |
0,0825 |
0,0796 |
0,0795 |
0,0777 |
0,0760 |
0,0766 |
0,0765 |
0,0738 |
0,0737 |
0,0765 |
|
|
P 4 |
0,1429 |
0,2273 |
0,1369 |
0,1544 |
0,1504 |
0,1524 |
0,1498 |
0,1474 |
0,1461 |
0,1460 |
0,1432 |
0,1427 |
0,1527 |
|
|
P 5 |
0,0601 |
0,2227 |
0,2315 |
0,2659 |
0,2599 |
0,2583 |
0,2528 |
0,2497 |
0,2496 |
0,2510 |
0,2459 |
0,2416 |
0,2423 |
|
|
P 6 |
0,0337 |
0,1017 |
0,2683 |
0,2341 |
0,2383 |
0,2352 |
0,2374 |
0,2414 |
0,2509 |
0,2400 |
0,2457 |
0,2453 |
0,2399 |
|
|
P 7 |
0,0190 |
0,0536 |
0,1367 |
0,1231 |
0,1292 |
0,1327 |
0,1367 |
0,1386 |
0,1315 |
0,1380 |
0,1410 |
0,1453 |
0,1396 |
|
|
P 8 |
0,0109 |
0,0275 |
0,0692 |
0,0622 |
0,0652 |
0,0670 |
0,0693 |
0,0701 |
0,0691 |
0,0704 |
0,0729 |
0,0744 |
0,0716 |
|
|
P 9 |
0,0045 |
0,0118 |
0,0299 |
0,0258 |
0,0273 |
0,0270 |
0,0284 |
0,0291 |
0,0296 |
0,0296 |
0,0310 |
0,0311 |
0,0290 |
|
|
P 10 |
0,0014 |
0,0029 |
0,0075 |
0,0062 |
0,0067 |
0,0055 |
0,0068 |
0,0068 |
0,0064 |
0,0075 |
0,0075 |
0,0074 |
0,0069 |
ПРИЛОЖЕНИЕ Б
(справочное)
Процентные точки χ2 - распределений
Таблица Б.1- (1 - α) - квантили ![]() -распределения
-распределения
|
r |
α |
||||||||||
|
0,5 |
0,4 |
0,3 |
0,2 |
0,1 |
0,05 |
0,025 |
0,01 |
0,005 |
0,001 |
0,0005 |
|
|
1 |
0,455 |
0,708 |
1,074 |
1,642 |
2,706 |
3,841 |
5,024 |
6,635 |
7,879 |
10,828 |
12,116 |
|
2 |
1,386 |
1,833 |
2,408 |
3,219 |
4,605 |
5,991 |
7,378 |
9,210 |
10,597 |
13,816 |
15,202 |
|
3 |
2,366 |
2,946 |
3,665 |
4,642 |
6,251 |
7,815 |
9,248 |
11,345 |
12,838 |
16,266 |
17,730 |
|
4 |
3,357 |
4,045 |
4,878 |
5,989 |
7,779 |
9,488 |
11,143 |
13,277 |
14,860 |
18,467 |
19,997 |
|
5 |
4,351 |
5,132 |
6,064 |
7,289 |
9,236 |
11,070 |
12,832 |
15,086 |
16,750 |
20,515 |
22,105 |
|
6 |
5,348 |
6,211 |
7,231 |
8,558 |
10,645 |
12,592 |
14,449 |
16,812 |
18,548 |
22,458 |
24,103 |
|
7 |
6,346 |
7,283 |
8,383 |
9,803 |
12,017 |
14,067 |
16,013 |
18,475 |
20,278 |
24,322 |
26,018 |
|
8 |
7,344 |
8,351 |
9,524 |
11,030 |
13,362 |
15,507 |
17,535 |
20,090 |
21,955 |
26,125 |
27,868 |
|
9 |
8,343 |
9,414 |
10,656 |
12,242 |
14,684 |
16,919 |
19,023 |
21,666 |
23,589 |
27,877 |
29,666 |
|
10 |
9,342 |
10,473 |
11,781 |
13,442 |
15,987 |
18,307 |
20,483 |
23,209 |
25,188 |
29,588 |
31,420 |
|
11 |
10,342 |
11,530 |
12,899 |
14,631 |
17,275 |
19,675 |
21,920 |
24,725 |
26,757 |
31,264 |
33,136 |
|
12 |
11,340 |
12,584 |
14,011 |
15,812 |
18,549 |
21,026 |
23,336 |
26,217 |
28,300 |
32,909 |
34,821 |
|
13 |
12,340 |
13,636 |
15,119 |
16,985 |
19,812 |
22,362 |
24,736 |
27,688 |
29,819 |
34,528 |
36,478 |
|
14 |
13,339 |
14,685 |
16,222 |
18,151 |
21,064 |
23,685 |
26,119 |
29,141 |
31,319 |
36,123 |
38,109 |
|
15 |
14,339 |
15,733 |
17,322 |
19,311 |
22,307 |
24,996 |
27,488 |
30,578 |
32,801 |
37,697 |
39,719 |
|
16 |
15,338 |
16,780 |
18,418 |
20,465 |
23,542 |
26,296 |
28,845 |
32,000 |
34,267 |
39,252 |
41,308 |
ПРИЛОЖЕНИЕ В
(справочное)
Библиография
|
[1] |
Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с. |
|
[2] |
Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба//Теория вероятностей и ее применение. - 1973. - T. XVIII. - № 3. - С. 583 - 591 |
|
[3] |
Никулин М.С. О критерии хи-квадрат для непрерывных распределений/Теория вероятностей и ее применение. - 1973. - Т. XVIII. - № 3. - С. 675 - 676 |
|
[4] |
Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат//Заводская лаборатория. - 1992. - Т. 58. - № 3. - С. 52-58 |
|
[5] |
Aguirre N., Nikulin М . Chi-squared goodness-of-fit test for the family of logistic distributions//Kybernetika. - 1994. -V. 30.- №3. - P. 214 - 222 |
|
[6] |
Chernoff H., Lehmann E.L. The use of maximum likelihood estimates in y} test for goodness of fit//Ann. Math. Stat., 1954. - V. 25. - P. 579 - 586 |
|
[7] |
Чибисов Д. M. Некоторые критерии типа хи-квадрат для непрерывных распределений//Теория вероятностей и ее применение. - 1971. - Т. XVI. - № 1. - С. 3 - 20 |
|
[8] |
Рао С.Р. Линейные статистические методы и их применения. - М.: Наука, 1968. - 548 с. |
|
[9] |
Кокс Д., Хинкли Д. Теоретическая статистика. - М.: Мир, 1978. - 560 с. |
|
[10] |
Денисов В.И., Лемешко Б.Ю. Оптимальное группирование при обработке экспериментальных данных//Измерительные информационные системы. - Новосибирск, 1979. - С. 5 - 14 |
|
[11] |
Денисов В.И., Зачепа Г.Г., Лемешко Б.Ю. Об асимптотически оптимальном группировании при оценивании основного параметра гамма-распределения по группированным данным//Применение ЭВМ в оптимальном планировании и проектировании. - Новосибирск, 1974. - С. 50 - 53 |
|
[12] |
Лемешко Б.Ю. Об оценивании параметров распределений по группированным наблюдениям//Вопросы кибернетики. - М., 1977. - Вып. 30. - С. 80 - 96 |
|
[13] |
Лемешко Б.Ю. Об оценивании по частично группированным выборкам параметров распределения Эрланга//Применение ЭВМ в оптимальном планировании и проектировании. - Новосибирск, 1982. - С. 90 - 93 |
|
[14] |
Темешко Б.Ю., Панфилов А.Г., Панфилова Л.В. Асимптотически оптимальное группирование данных при анализе наблюдений, распределенных по законам Лапласа и двойного показательного//Математическое обеспечение стохастических и детерминированных моделей. - Новосибирск, 1986. - С. 15 - 23 |
|
[ 15] |
Лемешко Б.Ю. К вопросу решения задачи асимптотически оптимального группирования данных при обработке наблюдений, подчиняющихся бета-распределению//Машинные методы оптимизации, моделирования и планирования эксперимента. - Новосибирск, 1988. - С. 134 - 138 |
|
[16] |
Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов. В 2 ч. - Новосибирск: Изд-во НГТУ, 1993. - 347 с. |
|
[17] |
Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. - Новосибирск: Изд-во НГТУ, 1995. - 125 с. |
|
[18] |
Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев//Надежность и контроль качества. - 1997. - № 8. - С. 3 - 14 |
|
[19] |
Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия//Заводская лаборатория. - 1998. - Т. 64. - № 1 - С. 56 - 64 |
|
[20] |
Денисов В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть I. Критерии типа χ2. - Новосибирск: Изд-во НГТУ, 1998. - 126 с. |
|
[21] |
Mann Н .В ., Wald A. On the choice of the number of class intervals in the application of the chi square test//Ann. Math. Stat., 1942. V. 13. - P. 306 - 317. |
|
[22] |
Лемешко Б.Ю. Постовалов С.Н. Прикладные аспекты использования критериев согласия в случае проверки сложных гипотез//Надежность и контроль качества. - 1997. - № 11. - С. 3 - 17 |
|
[23] |
Лемешко Б.Ю. Постовалов С.Н. О зависимости предельных распределений статистик χ2 Пирсона и отношения правдоподобия от способа группирования данных//Заводская лаборатория. - 1998. - Т. 64. - № 5. - С. 56 - 63 |
|
[24] |
Лемешко Б.Ю. Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов//Заводская лаборатория. - 1998.-Т. 64.- № 3. - С. 61 - 72 |
|
[25] |
Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - Л.: Энергоатомиздат, 1991. - 303 с. |
|
[26] |
Cochran W. G. Some Methods of Strengthening the Common χ 2 Tests//Biometrics, 1954. - V. 10. - P. 417 |
|
[27] |
Mann H.В ., Wald A. On the choice of the number of intervals in the application of the chi-square test//Ann. Math. Stat., 1942. - V. 13. - P. 478 - 479 |
|
[28] |
Sturgess H.A. The choice of classic intervals//J. Am. Statist. Assoc. - March 1926. - 47 p. |
|
[29] |
Шторм P. Теория вероятностей. Математическая статистика. Статистический контроль качества. - М.: Мир, 1970. - 368 с. |
|
[30] |
Heinhold I., Gaede К .W. Ingeniur statistic. - Munchen; Wien, Springier Verlag, 1964. - 352 s. |
|
[31] |
Таушанов З., Тонева E., Пенова P. Вычисление энтропийного коэффициента при малых выборках//Изобретательство, стандартизация и качество. - 1973. - № 5. - София |
|
[32] |
Тонева Е. Аппроксимация распределений погрешности средств измерений//Измерительная техника. - 1981. - №6. - С. 15 - 16 |
|
[33] |
Алексеева И.У. Теоретическое и экспериментальное исследование законов распределения погрешностей, их классификация и методы оценки их параметров: Автореф. дис. на соиск. учен, степени кан. техн. наук. - Л., 1975. - 20 с. |
|
[34] |
Бурдун Г.Д., Марков Б.Н. Основы метрологии. - М.: Изд-во стандартов, 1985. - 120 с. |
|
[35] |
Ченцов Н.Н. Статистические решающие правила и оптимальные выводы. - М.: Наука, 1972. - 520 с. |
|
[36] |
Чибисов Д.М., Гванцеладзе Л.Г. О критериях согласия, основанных на группированных данных// III советско-японский симпозиум по теории вероятностей. - Ташкент: Фан, 1975. - С. 183 - 185 |
|
[37] |
Боровков А.А. О мощности критерия χ2 при увеличении числа групп//Теория вероятностей и ее применение. - 1977. - Т. XXII. - № 2. - С. 375 - 378 |
|
[38] |
Лемешко Б.Ю., Чимитова Е.В. Максимизация мощности критериев типа χ2//Доклады Сибирского отделения Академии наук высшей школы. - Новосибирск, 2000. - № 2. - С. 53 - 61 |
|
[39] |
Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с. |
Ключевые слова: проверка гипотез, простые и сложные гипотезы, критерии согласия, группирование данных, асимптотически оптимальное группирование данных, уровень значимости, конкурирующая гипотеза, мощность критерия