Количественные свойства товаров
Количественные свойства принято называть величинами, а их проявления называют значениями величины. Величины группируются в три подкласса:
■ неархимедовы;
■ скалярные;
■ многомерные.
Неархимедовы величины описываются соотношениями «больше-меньше», но к ним не применимо понятие пропорциональности, то есть невозможно установить, во сколько раз одно проявление свойства больше или меньше другого проявления. Для неархимедовых величин не обязательно наличие нуля. В математике это выражают так: для неархимедовых величин не выполняется аксиома Евдокса (или аксиома Архимеда): каковы бы ни были величины «а» и «b» одного и того же рода, существует такое натуральное число «n»,что а < nb при а > b.
Дискретными неархимедовыми величинами являются числа твердости по шкале Мооса, баллы силы землетрясений по шкале наблюдаемых разрушений. Непрерывные неархимедовы величины — это числа твердости по шкалам Бринелля, Роквелла, Виккерса и Шора, кислотные, бромные и йодные числа, октановые и цетановые числа, числа светочувствительности фотоматериалов.
Примеры измерительных инструментов: специальные приборы для измерения числа падения, характеризующие хлебопекарное качество муки.
Скалярные величины наиболее широко используются для количественного описания свойств. Они включают величины:
■ счетные;
■ пропорциональные;
■ аддитивные;
■ интервальные;
■ относительные.
Счетные величины выражаются положительными целыми числами, они могут быть однородными (например, электроны, яблоки) и разнородными (например, упаковки различного вида). Единицей измерения для счетных величин служит арифметическая единица. Для измерения числа изделий существуют счетчики, применяемые в учетных операциях.
Пропорциональные величины выражаются непрерывным множеством положительных действительных чисел, начиная с нуля. Для этих величин имеет смысл суждение «во сколько раз больше или меньше», и, следовательно, операции арифметического вычитания, умножения и деления, но не имеет смысла операция сложения. Примером пропорциональной величины является термодинамическая температура: складывать термодинамические температуры нет смысла.
Измерительные инструменты для пропорциональных величин:

Аддитивные величины также выражаются непрерывным множеством положительных действительных чисел. К этим величинам применимы все арифметические операции, включая сложение. Например, можно складывать массы объектов.
Понятия о счетных, пропорциональных и аддитивных величинах содержат в себе привычное логическое представление о нуле.
Измерительные инструменты для аддитивных величин:
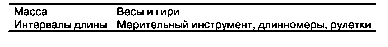
Интервальные величины отличаются тем, что для них невозможно логически обоснованно определить нулевое количество, однако интервалы таких величин имеют логическую структуру пропорциональных или аддитивных величин и поэтому имеют нуль. Известный пример интервальной величины — текущее время, счисление которого ведется от условного нуля, а интервалы времени могут иметь нулевое значение. Складывать интервалы времени можно, но складывать даты событий бессмысленно.
Измерительные инструменты для интервальных величин:
Текущее время
Хронометры, часы
Относительные величины являются отношениями двух произвольных количественных проявлений одного и того же свойства. Относительными величинами являются разнообразные коэффициенты (пропускания, отражения, усиления), глубина модуляции, добротность, коэффициент полезного действия, вероятность, критерии подобия, размеры плоского и телесного углов, а также кратные и дольные величины. Измерительными инструментами для коэффициента пропускания, например, являются фотометры. Примеры приведены в табл.

Многомерные величины могут быть двухмерными, трехмерными (векторы) и другой различной мерности, свойственной математическим понятиям различных видов. Примерами конкретных свойств, которые являются двухмерными величинами, являются: импеданс, характеризуемый совокупностью активной и реактивной составляющих (или модулем и фазой) полного сопротивления; давление крови человека, характеризуемое совокупностью верхнего и нижнего давлений. Трехмерными величинами (векторами) являются скорость и ускорение движения в пространстве, сила, напряженность электрического поля и т. д.